Непрерывные случайные величины. Системы случайных величин. Функция двух случайных аргументов. Формула свертки. Устойчивость нормального распределения, страница 2

.

         

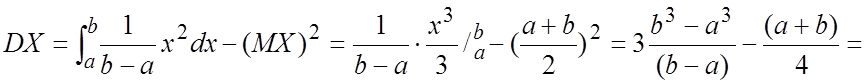
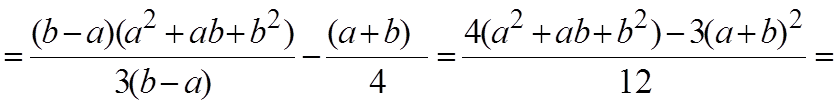
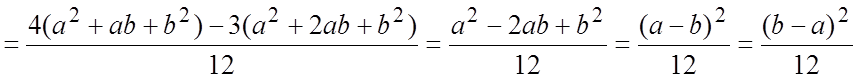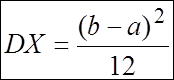
Пример 5. Пусть случайная величина Х имеет нормальное распределение X~N(a, G²). Найти дисперсию DX.

X~N(a, G²). MX=a.

.

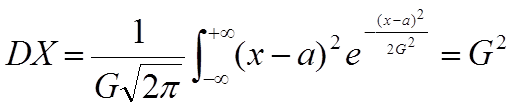Таким образом, .

Пример 6. Пусть случайная величина Х имеет показательное распределение 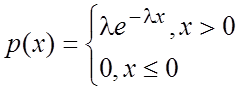. Найти DX.

^.

.

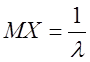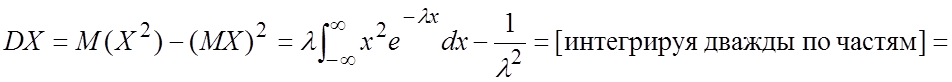
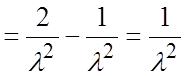Таким образом, .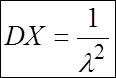

Теорема 1. Если случайная величина Х имеет нормальное стандартное распределение с параметрами (a, G²), то случайная величина 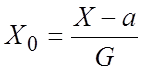 имеет нормальное распределение, т.е. .

; .

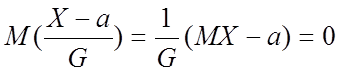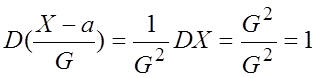Теорема 2. (Критерий независимости дискретных случайных величин).

Для того чтобы дискретные случайные величины Х₁,…,Х_n были независимы, необходимо и достаточно, чтобы для любых действительных чисел х₁,…,х_n  выполнялось  соотношение .

Теорема 3. (Критерий независимости для непрерывных случайных величин).

Для того чтобы непрерывные случайные величины Х₁, Х₂,…,Х_n были независимыми, необходимо и достаточно, чтобы для любых действительных чисел х₁,…,х_n выполнялось соотношение

.

Здесь —совместимая плотность распределения случайных величин Х₁,…,Х_n, то есть совместимая функция распределения случайных величин Х₁,…,Х_n

.

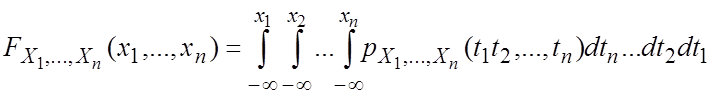Предположим, что случайная величина . Вероятность, что

.

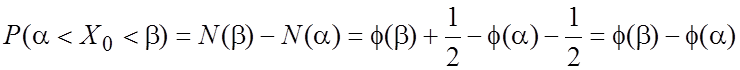Пусть .

.

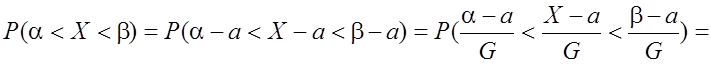
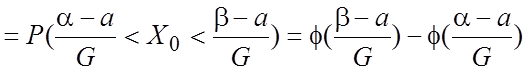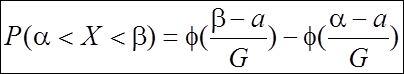          , где —функция Лапласа.

  Замечание. Необходимо отметить, что φ(t)—четная функция, т.е.

φ(-х)=φ(х); функция Лапласа —нечетная, т.е.; функция стандартного нормального распределения N(x) обладает свойством N(x)+N(-x)=1.

§ 16. Системы случайных величин.

o  Вектор , где —случайные величины, называются n-мерным случайным вектором.

Таким образом, случайный вектор  отображает пространство элементарных исходов Ω→IRⁿ в n-мерное действительное пространство IRⁿ.

o  Функция

 называется функцией распределения случайного вектора  или совместной функцией распределения случайных величин .

Свойства функции распределения случайного вектора.

Свойство 1.  .

Свойство 2.  Функция распределения случайного вектора неубывающая по каждому аргументу.

Пусть x₁<y₁, тогда событие .

Тогда . По свойству вероятности если , то , получим . Т.е. функция не убывает по первому аргументу. Аналогично для любого аргумента.

Свойство 3.  .

=0

Свойство 4.   

.

         

         

         

          =.

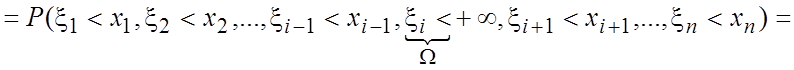
o  Случайный вектор называется дискретным, если все его компоненты—дискретные случайные величины.

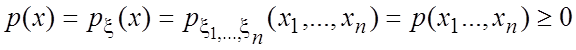o  Случайный вектор  называется непрерывным, если существует неотрицательная функция , называется плотностью распределения случайных величин  такая, что функция распределения .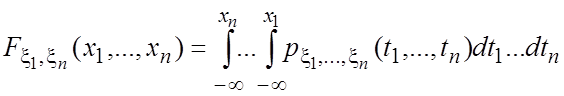

Свойства плотности распределения случайного вектора.

Свойство 1. 

Свойство 2.  .

  .

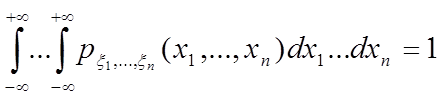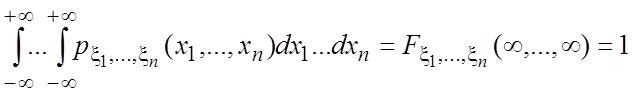Теорема 1. Пусть —непрерывный случайный вектор. Тогда случайные величины  и —непрерывны, причем ,  .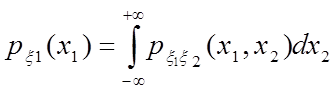

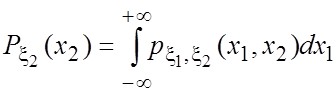Свойство 3. 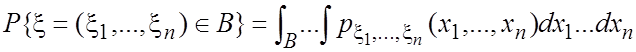 , где —множество из пространства IRⁿ.

o  Говорят, что случайный вектор  имеет равномерное распределение в области , если она непрерывна и имеет плотность.

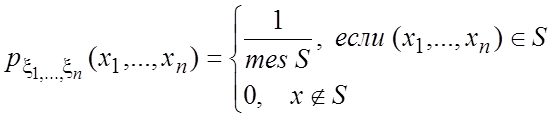
Если множество

.

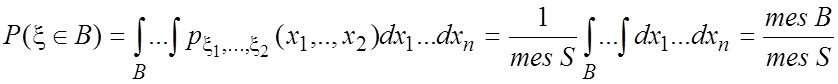o  Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента Х.

Теорема 2. Пусть случайная величина Х непрерывна с плотностью , а случайная величина , где —монотонная дифференцируемая функция, тогда случайная величина Y—непрерывная и имеет плотность .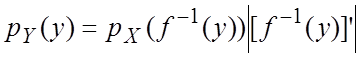

а) Пусть функция  возрастает. По определению

.

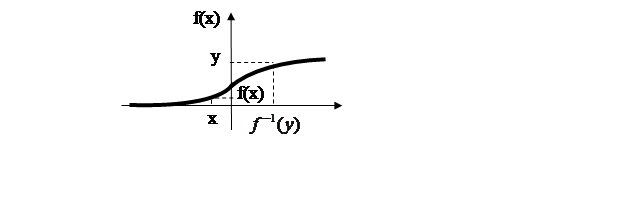
Продифференцируем обе части. Справа получим: , слева— , что и требовалось .

б) Пусть  убывает.

.

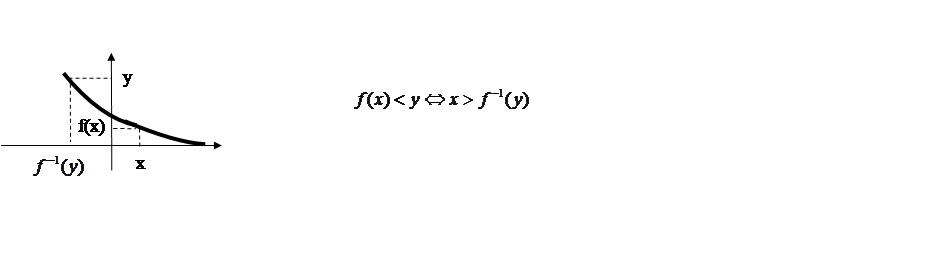
Продифференцировав обе части, .

          Покажем, как найти распределение функции случайного аргумента. Пусть аргумент Х—дискретная случайная величина

А) Если различным возможным значениям аргумента функции Y, то вероятность соответствующих значений X и Y между собой равны.

Пример 1. Дискретная случайная величина Х задана распределением

Х	2	3
Р	0,6	0,4

Найти распределение функции .

Решение. Найдем возможные значения Х:

, . Искомое распределение Y:

Y	4	9
P	0,6	0,4

Б) Если различным возможным значениям Х соответствуют значения Y, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений Y.

Пример 2. Дискретная случайная величина Х задана распределением

Х	-2	2	3
Р	0,4	0,5	0,1

Найти распределение функции .

, .

Вероятность возможного значения y₁=4 равна сумме вероятностей несовместимых событий Х₁=-2, Х₂=2, т.е. 0,4+0,5=0,9. Вероятность возможного значения y₂=9 равна 0,1. Напишем искомое распределение Х.

Y	4	9
P	0,9	0,1