◄ Действительно, пусть для множества М запись Р(М) означает, что М не содержит себя в качестве своего элемента. Рассмотрим класс К = {M: P(M)} множеств, обладающих свойством Р, то есть не содержащих себя в качестве элемента. Если К – множество, то либо верно Р(К), либо верно ù Р(К). Однако эта альтернатива для К невозможна. Действительно, если верно Р(К), то К не содержит К в качестве своего элемента, а тогда по определению К К нужно считать элементом К!. Если же ù Р(К), то есть К – элемент множества К, то по определению множества К К нельзя считать элементом К. Следовательно, К не множество. ►
Это классический парадокс Рассела, один из тех парадоксов, к которым приводят наивные представления о множестве.
3.2. Отношение включения. Высказывание "х есть элемент множества Х" коротко обозначают символом х Î Х (или Х ' х), а его отрицание х Ï Х.
В записи высказываний о множествах часто используются логические операторы $ ("существует" или "найдется") и " ("любой" или "для всякого"), называемые кванторами существования и общности соответственно.
Например, запись " х ((хÎА) Û (хÎВ)) означает, что для любого объекта х соотношения хÎА и хÎВ равносильны.
Отношение включения определяется так:
(АÌВ) := "х ((хÎА) Þ (хÎВ)) (любой элемент множества А является элементом множества В). При этом говорят, что А является подмножеством множества В. Запись В É А означает, что В включает в себя А.
Диаграмма Венна.
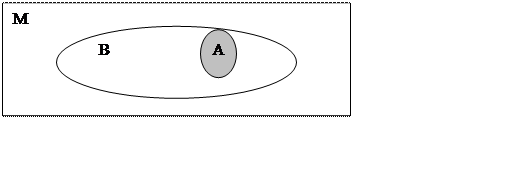 |
АÌВ
(А=В) Û (АÌВ) Ù (ВÌА)
{xÎM: P(x)} – подмножество множества М, элементы которого обладают свойством Р.
Æ – знак пустого множества (это множество, определяемое каким-либо свойством, которое не выполняется ни для одного элемента).
3.3. Простейшие операции над множествами.
Пусть А и В – подмножества множества М.
а) Объединением множеств А и В называется множество
АÈВ := {xÎM: (xÎA) Ú (xÎB)}.
б) Пересечением множеств А и В называется множество
АÇВ := {xÎM: (xÎA) Ù (xÎB)}.
в) Разностью множеств А и В называется множество
А\В := {xÎM: (xÎA) Ù (xÏB)}.
г) СМА := М\А – дополнение А в М. (От слова комплимент – дополнение).
Пример. Иллюстрацией взаимодействия введенных понятий являются следующие соотношения – так называемые правила де Моргана. (А. де Морган – шотландский математик, 1806-1871):
1) СМ(АÈВ) = СМА Ç СМВ;
2) СМ(АÇВ) = СМА È СМВ.
Доказать самостоятельно.
Упражнения. Пусть X, Y Ì M. Проверить соотношения.
1) C(CX) = X.
2) X Ì Y Û CY Ì CX.
3) X Ç Y = Æ Û X Ì CY Û Y Ì CX.
4) X È Y = M Û CX Ì Y Û CY Ì X.
§ 4. Понятие функции
4.1. Введение. Примеры функций:
s(t)=s0+v0t+at2/2;
V(t)=v0(1+at);
p=const.
Задачей настоящего параграфа является формирование определения функции, опирающегося в конечном счете на одно неопределяемое понятие, а именно, понятие множества.
4.2. Понятие упорядоченной пары.
Определение 1. Упорядоченной парой (х; у) элементов х и у называется множество {{x}; {x; y}}. При этом х называется первой, а у – второй координатой упорядоченной пары. Итак,
(х; у) := {{x}; {x; y}}.
Таким образом, упорядоченная пара – это двухэлементное множество, один из элементов которого есть неупорядоченная пара {x; y}, а другой элемент {x} указывает, какой из членов этой неупорядоченной пары считать первым.
Упорядоченная тройка элементов: (х; у; z) := ((x; y); z).
При n ³ 3 упорядоченный набор из n элементов (n-ка) определяется так:
(x1; x2; …; xn-1; xn) := ((x1; x2; …; xn-1); xn).
Две упорядоченные пары (х; у) и (u;v) равны в том и только в том случае, когда х=u b y=v, то есть
((х; у) = (u;v)) Û (х=u Ù y=v).
Если х ¹ у, то (х; у) ¹ (у; х) (даже если х и у – элементы одного множества).
Кроме того, (х; х) ¹ {x}, хотя {x; x} = {x}.
4.3. Декартово произведение множеств. Прямым или декартовым произведением Х´У множеств Х и У называется множество всевозможных упорядоченных пар (х; у), образованных из элементов х множества Х и элементов у множества У. Таким образом,
Х´У := {(x;y): xÎX и yÎY};
((x; y)ÎX´Y) Û (xÎX Ù yÎY).
Элементом декартова произведения является упорядоченная пара.
Пример. Х = {лебедь, щука, рак}, Y = {заяц, волк}.
Х´У = {(лебедь, заяц), (лебедь, волк), (щука, заяц), (щука, волк), (рак, заяц), (рак, волк)}.
У´Х = {(заяц, лебедь), (заяц, щука), (заяц, рак), (волк, лебедь), (волк, щука), (волк, рак)}.
У´У = {(заяц, волк), (заяц, заяц), (волк, заяц), (волк, волк)}.
В общем случае декартово произведение множеств не коммутативно.
Если Х¹У, то Х´У¹У´Х.
X´Y´Z := {(x; y; z): xÎX Ù yÎY Ù zÎZ}.
Если Х1=Х2=...=Хn=X, то Х1´Х2´...´Хn=Xn – декартова степень множества Х.
4.4. Бинарное отношение.
Отношениями называются подмножества декартова произведения
Определение. Бинарным (двуместным) отношением называется подмножество Uf декартова произведения Х´У: Uf Ì Х´У. Говорят, что элемент хÎХ находится в отношении f к элементу уÎУ – обозначение xfy – в том и только в том случае, когда упорядоченная пара (х; у)Î Uf..
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.