




Министерство образования Республики Беларусь
Учреждения образования
«Гомельский государственный университет им Ф. Скорины»
Отчет по лабораторной работе
ИЗУЧЕНИЕ ФИЗИЧЕСКОГО МАЯТНИКА.
Выполнили студенты группы Ф-11: Курьян В.Ю.
Паутов В.A.
Проверил преподаватель: Соколов С.И.
2011
ИЗУЧЕНИЕ ФИЗИЧЕСКОГО МАЯТНИКА
ЦЕЛЬ РАБОТЫ: исследование законов колебательного движения физического маятника и определение ускорения свободного падения методом Бесселя.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: установка FPM-04, линейка.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Физическим маятником (ФМ) называется твёрдое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси. Точка
О пересечения этой оси с вертикальной плоскостью, проходящей через центр масс маятника, называется точкой подвеса.
Согласно основному уравнению динамики вращательного движения, в отсутствии сил сопротивления, уравнение движения ФМ имеет вид:
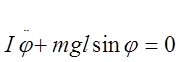 (1)
(1)
где I - момент инерции маятника относительно оси качания,
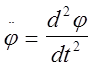 -
угловое ускорение маятника,
-
угловое ускорение маятника,
m - масса маятника,
l - расстояние от точки подвеса до центра масс маятника.
Ограничиваясь случаем малых
углов (![]() ) из (1) имеем
) из (1) имеем
![]() (2)
(2)
где введено обозначение 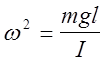
Нетрудно убедится, что решением записанного дифференциального уравнения (2) является функция
![]()
т.е. угол j отклонения ФМ от вертикали изменяется по гармоническому закону. Следовательно период колебаний ФМ равен
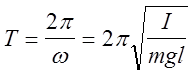 (3)
(3)
Как известно, период математического маятника
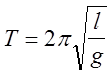 (4)
(4)
Сравнивая (3) и (4) находим, что ФМ колеблется с тем же периодом, что и математический, имеющий длину
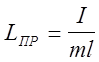 (5)
(5)
Длина
математического маятника ![]() , имеющего тот же период
колебаний, что и данный ФМ, называется приведённой длиной физического маятника.
, имеющего тот же период
колебаний, что и данный ФМ, называется приведённой длиной физического маятника.
Момент инерции тонкого стержня относительно оси,
проходящей через центр масс С перпендикулярно плоскости рисунка, равен 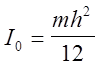 . По теореме Штейнера находим, что момент
инерции стержня относительно оси качаний
. По теореме Штейнера находим, что момент
инерции стержня относительно оси качаний
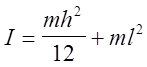 (6)
(6)
Подставим (6) в (4) и (5), приходим к соотношению
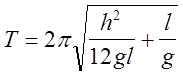 (7)
(7)
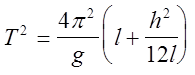 (8)
(8)
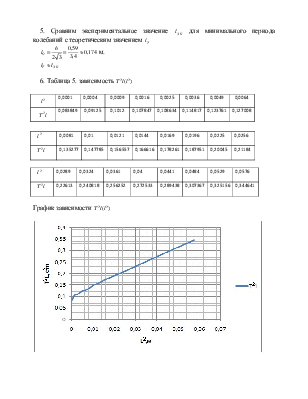
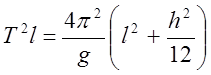 (9)
(9)
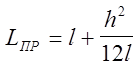 (10)
(10)
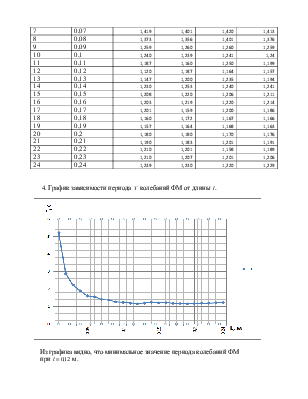
удобном для анализа и экспериментальной проверки. В частности, из анализа на экстремум функции (7) следует, что при
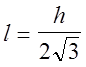 (11)
(11)
период Т физического маятника является минимальным.
ВЫПОЛНЕНИЕ РАБОТЫ
Упражнение № 1. Проверка формулы периода колебаний и определение приведённой длины физического маятника.
1. Таблица 1. Измерение времени 10 полных колебаний физического маятника, вычисление периода его колебаний.
|
№ опыта |
1 |
2 |
3 |
4 |
5 |
Среднее значение |
|
|
12,47 |
12,00 |
12,35 |
12,30 |
12,41 |
12.30 |
|
|
1,247 |
1,2 |
1,235 |
1,230 |
1,241 |
1.230 |
Погрешность измерений равна 3,7489%
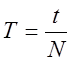 ,
, ![]()
2.
Длина физического маятника ![]() ,
,
Расстояние
от центра тяжести до точки подвеса ![]() .
.
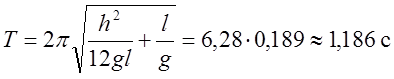 .
.
3.
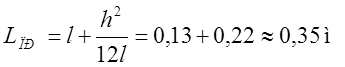 .
.
4. Таблица 2. Измерение времени 10 полных колебаний математического маятника, вычисление периода его колебаний.
|
№ опыта |
1 |
2 |
3 |
4 |
5 |
Среднее значение |
|
|
11,59 |
12,03 |
12,40 |
12,39 |
12,10 |
12,102 |
|
|
1,159 |
1,203 |
1,240 |
1,239 |
1,210 |
1,2102 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.