Изучение электрических процессов в простых цепях (Лабораторная работа № 9)

ЛАБОРАТОРНАЯ РАБОТА № 9

ИЗУЧЕНИЕ ЭЛЕКТРИЧЕСКИХ ПРОЦЕССОВ В ПРОСТЫХ ЦЕПЯХ

ЛАБОРАТОРНАЯ РАБОТА № 9

ИЗУЧЕНИЕ ЭЛЕКТРИЧЕСКИХ ПРОЦЕССОВ В ПРОСТЫХ ЦЕПЯХ

Цель работы: научиться измерять коэффициент передачи в простых цепях с помощью

осциллографа, исследовать входные и передаточные характеристики простых цепей с одним реактивным элементом, научиться определять диапазон частот, в которых входное сопротивление цепи имеет практически чисто резистивный или чисто реактивный характер.

ТЕОРИТИЧЕСКИЕ СВЕДЕНИЯ

Цепь, содержащая два резистора.

Схема (рис.9) представляет собой резистивный делитель, имеющий две пары внешних зажимов. Обозначим входные зажимыU₁ выходные U₂.Коэффициент передачи цепи по напряжению 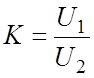. Коэффициент передачи К являетсяI важнейшей характеристикой цепи, поскольку дает возможность рассчитать напряжение на выходе по известному напряжению на входе.

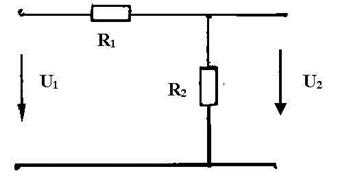
Рисунок 9.1

Зададимся для цепи (рис.9, 1 ) напряжением на входе U₁. Тогда действующее значение тока 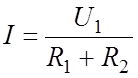. Действующее значение напряжение на выходе:

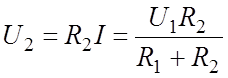         (9.1)

Коэффициент передачи:

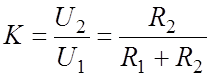                        (9.2)

или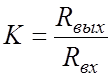

Если на вход резистивного делителя подавать сигнал различных частот с генератора, то, пренебрегая паразитными емкостями, можно установить, что коэффициент передачи не будет изменяться.

Запомните, в цепи с активным сопротивлении ток и напряжение совпадают по фазе. Электрическая мощность в активном сопротивлении преобразуется в тепло.

Цепь, содержащая R и C.

На рис.9.2. показан делитель напряжения из конденсатора и резистора. Согласно закону Ома для комплексных величин, комплексный входной ток

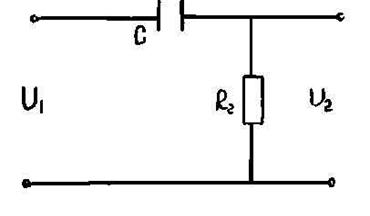
Рисунок 9.2

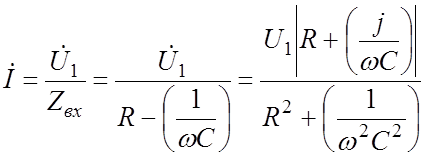
Напряжение на резисторе R равно

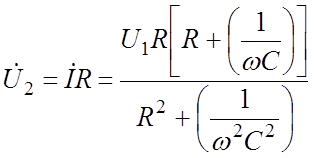       (9.3)

Сравните полученный результат с выражением для резистивного целителя (9.1.).

Для постоянного тока идеальный конденсатор представляет собой сопротивление (активное) R=¥, не позволяющее протекать постоянному току. На переменном токе с частоfой f реактивное сопротивление конденсатора C или емкостное сопротивление выражается формулой:

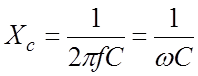
Реактивное сопротивление вызывает сдвиг фаз между током и напряжением (ток в цепи с емкостью без активного сопротивления опережает напряжение на 90°). В цепи, содержащей R и C, сдвиг фаз между током и напряжением будет меньше 90° .

Возвращаясь к рис.9.2. заметим, что входное сопротивление 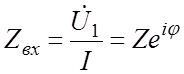. При изменении частоты сопротивление реактивных .элементов цепи изменяется. Зависимость модуля комплексного входного сопротивления цепи от частоты называют входной амплитудно - частотной характеристикой цепи (АЧХ): Z_вх=Z_вх(w). Аналогично, входной фазочастотной характеристикой цепи (ФЧХ) называют зависимость аргумента комплексного входного сопротивления от частоты j_Zвх=j(w).

Комплексное входное сопротивление можно представить не только и показательной Z_вх=Z_вхe^ij, но и в алгебраической форме Z_вх=R_вх+jX_вх резистивная и реактивная составляющая комплексного входного сопротивления. Частоту w_гр, на которой реактивная составляющая входного сопротивления цепи по абсолютному значению равна резистивной составляющей, называют граничной.

График АЧХ для схемы (рис. 9.2) представлен на рис. 9.3. Как вы видите, график представляет фильтр высоких частот. На высоких частотах выходное напряжение приблизительно равно входному: 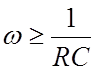, а на низких частотах выходное напряжение уменьшается до нуля.

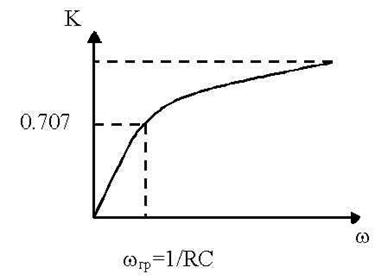
Рисунок 9.3

Если поменять местами R и C, то фильтр будет будет вести себя противоположым образом в отношении частоты, получим фильтр низких частот (рис. 9.4).

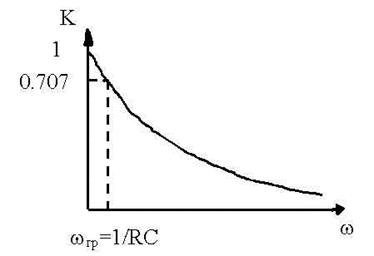
Рисунок 9.4

Для схемы (9.2)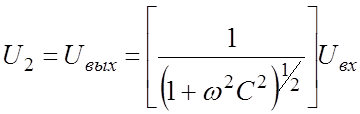

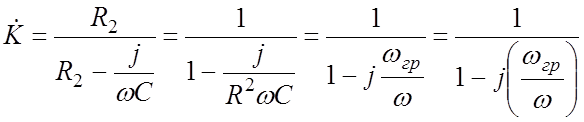         (9.4)

отсюда передаточная АЧХ

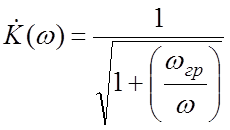         (9.5)

а ФЧХ

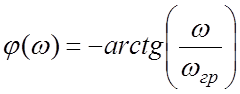       (9.6)

Цепь содержащая R и L.

Очевидно, что в RL - цепи

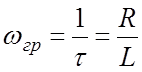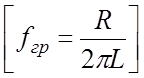;           (9.7)

а RC - цепи

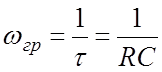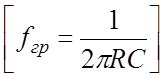;    (9.8)

для RL - цепи

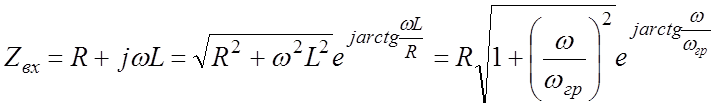            (9.9)

Итак, входную АЧХ последовательной RL - цепи вычисляют согласно выражению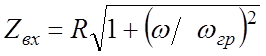, а входную фазочастотную характеристику   (9.10)