Многоэтажное промышленное каркасное здание с применением сборных железобетонных элементов, страница 3

                 2.2  Осевому растяжению

  3.  Коэффициенты условий работы бетона ==0.9 [ 2, Табл. 15]

4.  Расчетные сопротивления в проекте приняты с учетом [2, п. 2.11]:

5.  Начальный модуль упругости бетона принят с учетом условий твердения бетона и класса В30 по прочности на сжатие [2, Табл. 18]

Е_в·10^-3=29,0 МПа; 

Е_в=29000МПа.

3.2 Арматура

Нормативные и расчетные сопротивления рабочей арматуры класса А-III:

1.  Нормативные сопротивления  [2, Табл. 19]     

2.  Расчетное сопротивление  (для D=6-8мм) и

  (для D=10-40мм).  [2, Табл. 22]

               3. Коэффициент условий работы арматуры класса А-III

                   [2, Табл. 24].

  4. Модуль упругости класса А-III:

  5. Расчетное сопротивление проволочной арматуры класса Вр-I:

      R_s=410МПа.  [2, Табл. 23]

6.  Модуль упругости арматуры класса Вр-I: E_s=17·10⁴ МПа. [2, Табл. 29]

4 Конструктивные требования

На рисунке 4.1 показана толщина защитного слоя бетона и минимальные расстояния между стержнями.

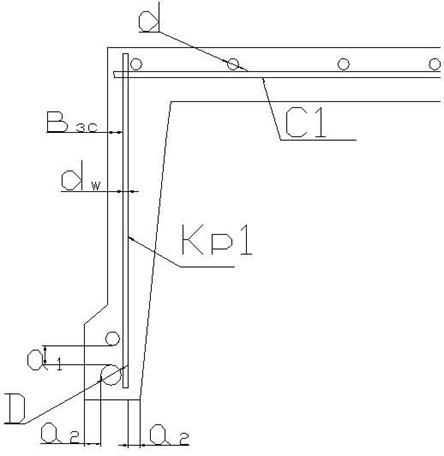
Рисунок 4.1 – Расположение сетки С1 и каркаса Кр1 в ребристой плите покрытия

d_w – диаметр поперечной арматуры в каркасе;

a₁ – расстояние в свету между отдельными стержнями продольной арматуры;

а₂ – защитный слой бетона продольной рабочей арматуры;

в_зс – защитный слой бетона для поперечной, распределительной и конструктивной арматуры.   

Толщины защитных слоев:

≥D           ≥D             в_зс≥dw

≥25          ≥20            в_зс≥15

                                       [2, п.5.12а]     [2,п.5.5]      [2,п.5.6]

На рисунке 4.2 показано размещение стержней арматуры по длине  и ширине изделия для возможности свободной укладки в форму цельных арматурных стержней, сеток или каркасов, идущих по всей длине или ширине изделия. Концы этих стержней должны отстоять от грани элемента при размере изделия до 9м – на 9 мм, до 12м – на 15мм, а свыше 12м – на 20мм.

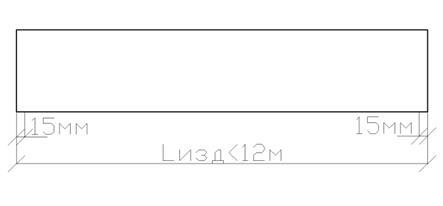
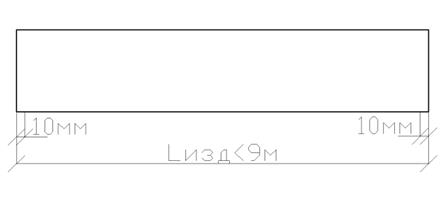
    Рисунок 4.2 – Размещение продольных стержней в плите перекрытия

 по [2, п.5.9]

    К трещинностойкости плиты перекрытия предъявляются требования по 3 категории. [2, П.1.16]

    Плита эксплуатируется в закрытом помещении по [2, Табл. 2]. Для арматуры класса А-III: а_crc1=0,4мм;  а_crc2=0,3мм, где:

а_crc1 – непродолжительная предельная ширина раскрытия трещин;

а_crc2 – продолжительная предельная ширина раскрытия трещин.

    Предельно допустимый прогиб определяется по СНиП 2.01.07-85 [1]:

Таблица 4.1 – Зависимость вертикального предельного прогиба от длины элемента

Длина элемента	lu≤ 1м	l=3м	l=6м	l=24м
Вертикальный предельный прогиб fu	l/120	l/150	l/200	l/250

    Для промежуточных значений прогибы определяются интерполяцией.

l_u=l_стр.к.-40см=6,5м (при заданном шаге =6,9м).

    Определим предельный прогиб для заданной длины элемента:

Тогда: f_u=1/201,4.

    5  Расчёт плиты перекрытия по предельным состояниям первой группы – по прочности.

    5.1 Расчёт нагрузки от собственного веса плиты перекрытия

    Нормативная нагрузка от собственного веса плиты перекрытия определяется по конструктивным размерам и удельному весу [2. П.2.1] (ρ=2500кг/м³=25кН/м³).

    На рис. 5.1 показана схема опирания плиты перекрытия плиты П1 на ригели и её поперечное сечение.

                                                        , где:                                      (5.1)

l_к – конструктивная длина плиты;

l_н – номинальная длина плиты.

 

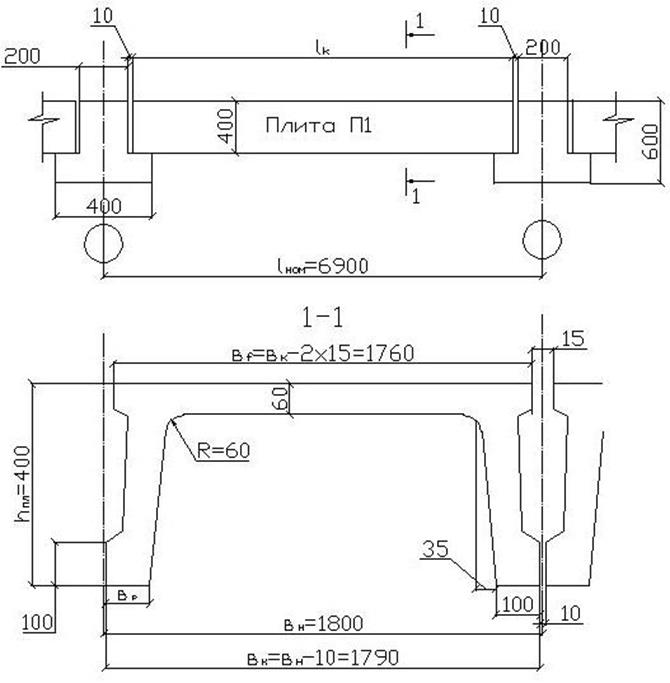
Рисунок 5.1 – Схема опирания и поперечное сечение плиты перекрытия П1

F=1,79·0,4-(1,59+1,52)·0,34· - 2·0,015·(0,205+0,175) = 0,176м²;

                                                       V=F·l_к;                                                      (5.2)

V=0,176·6,68=1,175м³

                                                       Р=V·γ;                                                       (5.3)

P=1,175·25=29,38кН;

G_п=, где:

F – площадь поперечного сечения плиты перекрытия П1, м²;

V – объём плиты перекрытия П1, м³;

G_п  - собственный вес плиты перекрытия П1.

.

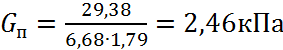   5.2  Расчёт прочности плиты по сечению, нормальному к продольной оси (расчёт на общий изгиб)