Расчет матрицы корреляции и ковариации для показателей прослушивающих и звукозаписывающих устройств

Задание № 2.9

Имеются статистические данные по 52 моделям прослушивающих и звукозаписывающих устройств по 5 показателям:

х1-цена

х2-качество звучания

х3-оснащение

х4-объем памяти

х5-вес

Требуется:

1.рассчитать матрицы корреляции и ковариации для исходных показателей;

2.рассчитать собственные значения L_i;

3.определить критерий информативности для использования различного числа главных компонент;

4.определить влияние главных компонент на первый признак;

5.вычислить значение оценок относительных ошибок прогноза показателей по 1 и 2 главным компонентам;

6.определить вклад главной компоненты в процентном отношении в суммарную дисперсию;

7.для интерпретации главных компонент построить матрицу нагрузок;

8.дать содержательную интерпретацию первых двух главных компонент, используя вращение осей координат главных компонент;

9.использовать центроидный метод.

Матрица исходных данных известна из предыдущего задания.

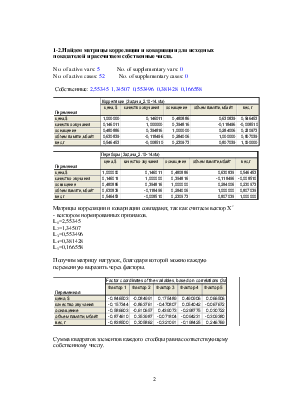
1-2.Найдем матрицы корреляции и ковариации для исходных показателей и рассчитаем собственные числа.

No. of active vars: 5            No. of supplementary vars: 0

No. of active cases: 52          No. of supplementary cases: 0

 Собственные: 2,55345  1,34507  0,553496  0,381428  0,166558 

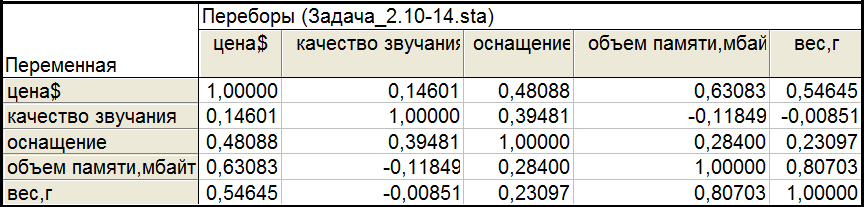
Матрицы корреляции и ковариации совпадают, так как считаем вектор Х^* - вектором нормированных признаков.

L₁=2,55345 

L₂=1,34507 

L₃=0,553496 

L₄=0,381428 

L₅=0,166558 

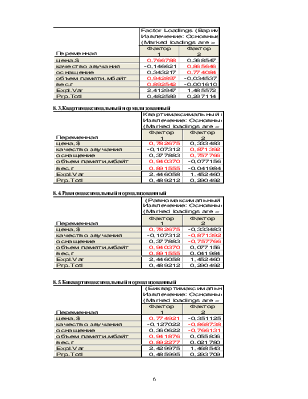
Получим матрицу нагрузок, благодаря которой можно каждую переменную выразить через факторы.

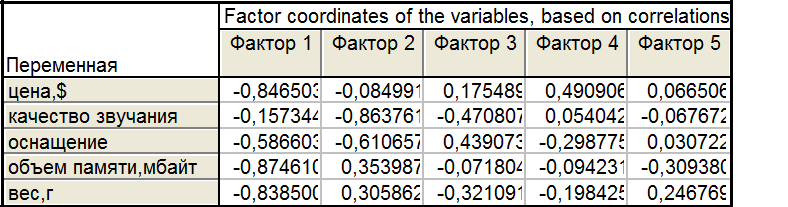
Сумма квадратов элементов каждого столбцы равна соответствующему собственному числу.

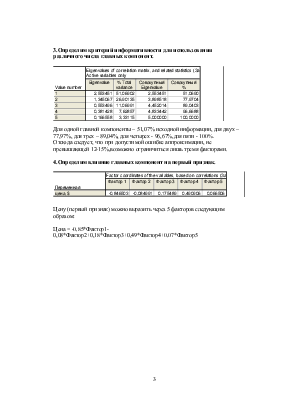
3.Определим критерий информативности для использования различного числа главных компонент.

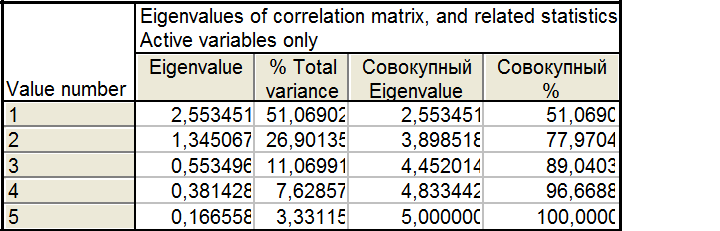
Для одной главной компоненты – 51,07% исходной информации, для двух – 77,97%, для трех – 89,04%, для четырех - 96,67%,для пяти - 100%.

Отсюда следует, что при допустимой ошибке аппроксимации, не превышающей 12-15%,возможно ограничиться лишь тремя факторами.

4.Определим влияние главных компонент на первый признак.

Цену (первый признак) можно выразить через 5 факторов следующим образом:

Цена = -0,85*Фактор1-0,08*Фактор2+0,18*Фактор3+0,49*Фактор4+0,07*Фактор5

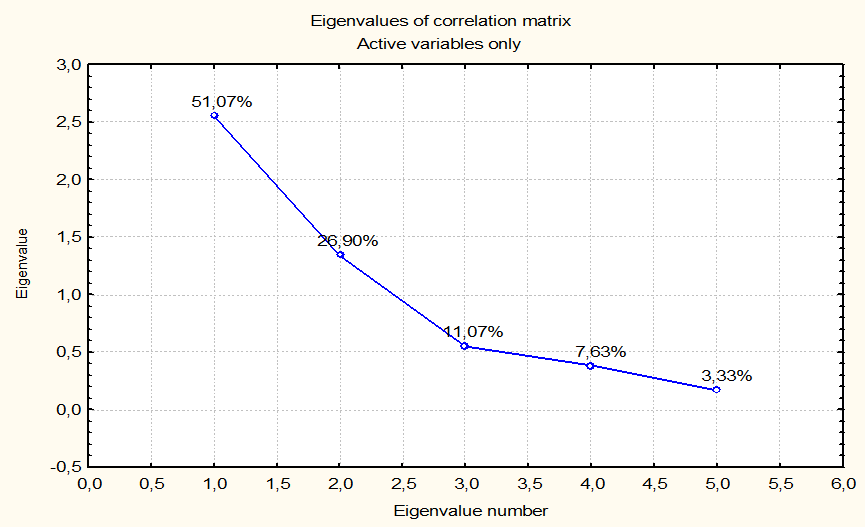
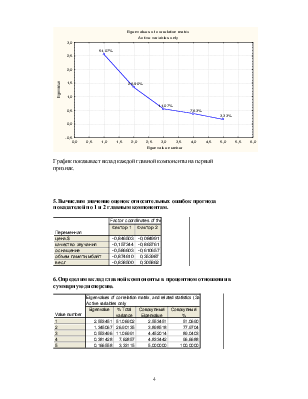
График показывает вклад каждой главной компоненты на первый признак.

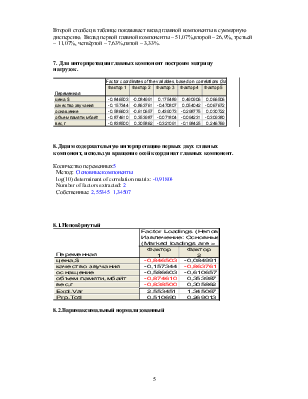
5.Вычислим значение оценок относительных ошибок прогноза показателей по 1 и 2 главным компонентам.

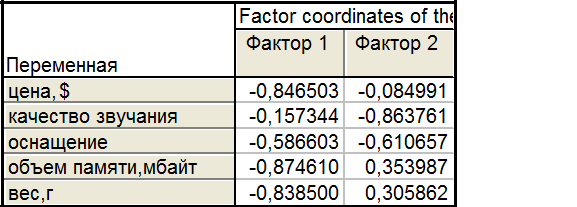
6.Определим вклад главной компоненты в процентном отношении в суммарную дисперсию.

Второй столбец в таблице показывает вклад главной компоненты в суммарную дисперсию. Вклад первой главной компоненты – 51,07%,второй – 26,9%, третьей – 11,07%, четвёртой – 7,63%,пятой – 3,33%.

7. Для интерпретации главных компонент построим матрицу нагрузок.

8.Дадим содержательную интерпретацию первых двух главных компонент, используя вращение осей координат главных компонент.

Количество переменных5

  Метод:  Основные компоненты

  log(10) determinant of correlation matrix: -0,91804

  Number of factors extracted: 2

  Собственные: 2,55345  1,34507 

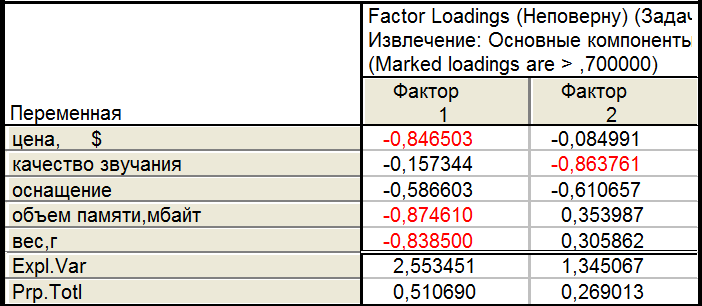
8.1.Неповёрнутый

8.2.Варимаксимальный нормализованный

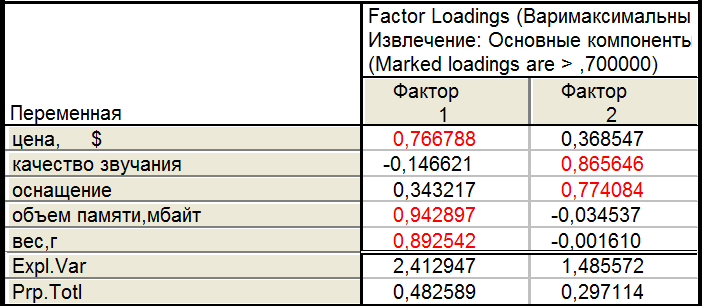
8.3.Квартимаксимальный нормализованный

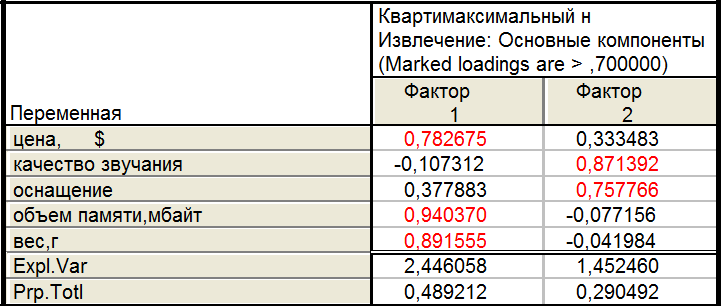
8.4.Равномаксимальный нормализованный

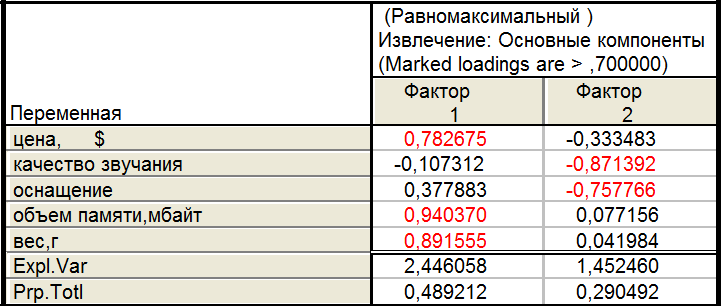
8.5.Биквартимаксимальный нормализованный

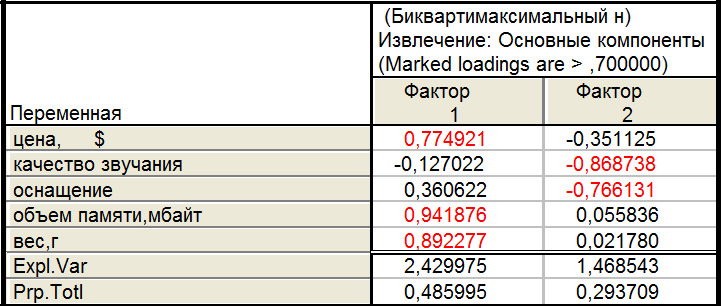
В ходе проведенного анализа, используя вращение осей координат главных компонент, мы получили 5 различных результатов.

При этом, квартимаксимальный поворот и равномаксимальный поворот дают схожие результаты, различающиеся лишь знаками второго фактора.

 В четырех случаях поворотов (за исключением неповернутого) значимые признаки каждого из факторов можно объединить в 2 группы – в первую входят объем памяти и вес, во вторую -  качество звучания и оснащение, в общем случае их можно назвать как «технические характеристики» и «внешние характеристики».

В  случае «неповернутый» вторая главная компонента слабо отображает исходные данные, поэтому он не является оптимальным. Наиболее оптимальным вариантом ,на мой взгляд, является Квартимаксимальный нормализованный, т.к. полученные с его помощью результаты наиболее полно отражают исходные данные, а положительные знаки указывают на положительное влияние признаков на результат.

9.Используем центроидный метод.

Количество переменных5

  Метод:  Principal factors (Centroid method)

  log(10) determinant of correlation matrix: -0,91804

  Number of factors extracted: 2

  Собственные: 2,17469  0,968258 

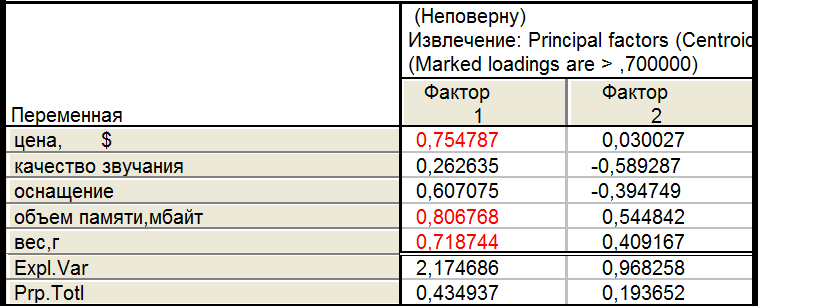
9.1.Неповёрнутый

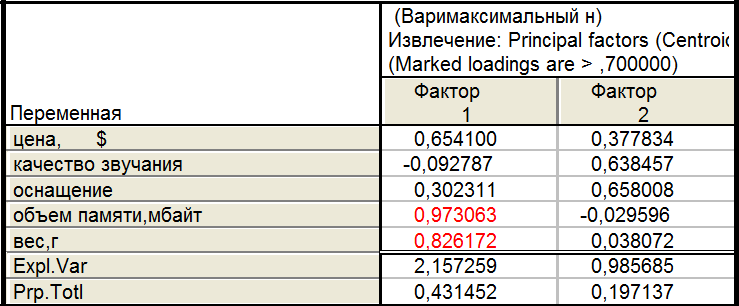
9.2.Варимаксимальный нормализованный

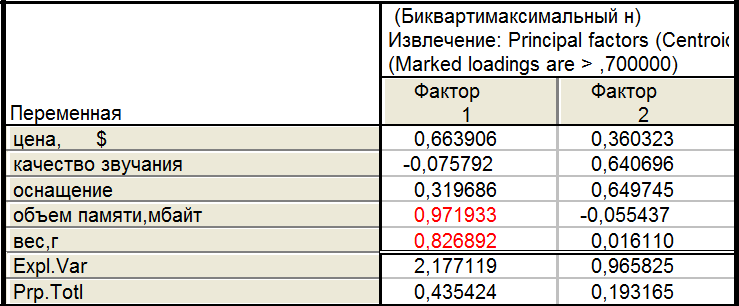
9.3.Биквартимаксимальный нормализованный

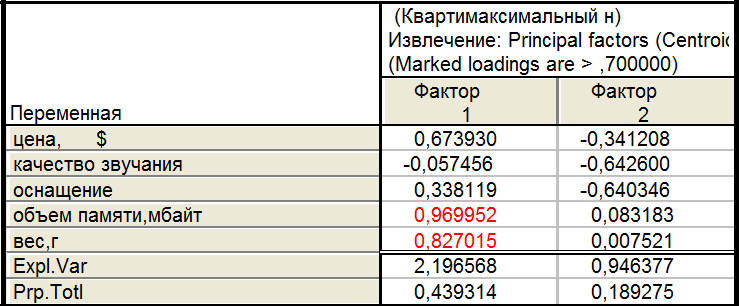
9.4.Квартимаксимальный нормализованный

9.5.Равномаксимальный нормализованный

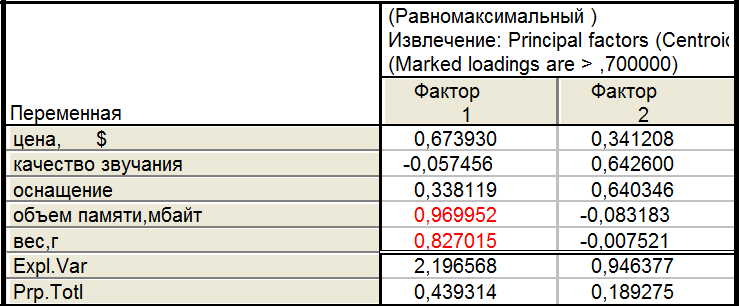
Ни один из вариантов не является оптимальным, так как ни в одном из них второй фактор не отображает исходные данные с необходимой информативностью.

Так как при двухфакторной модели происходит недопустимо большая потеря информации (22%),то перейдем к рассмотрению трехфакторной модели, которую в общем виде можно назвать: ценовой фактор, технические характеристики и внешние характеристики. В таком случае потеря информации не превышает 11%.

  Количество переменных5

  Метод:  Principal factors (Centroid method)

  log(10) determinant of correlation matrix: -,91804

  Number of factors extracted: 3

  Собственные: 2,20934  ,982353  ,122987 

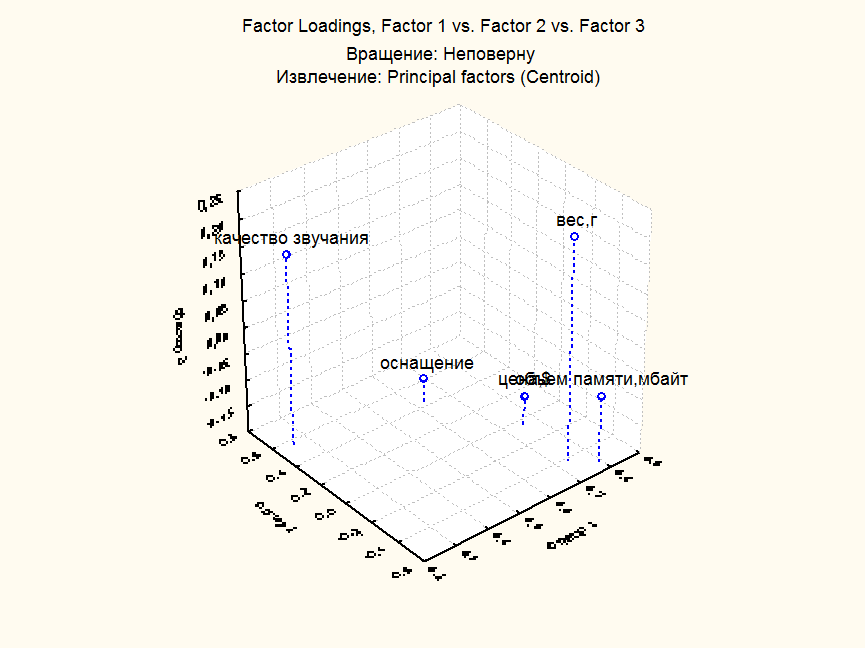
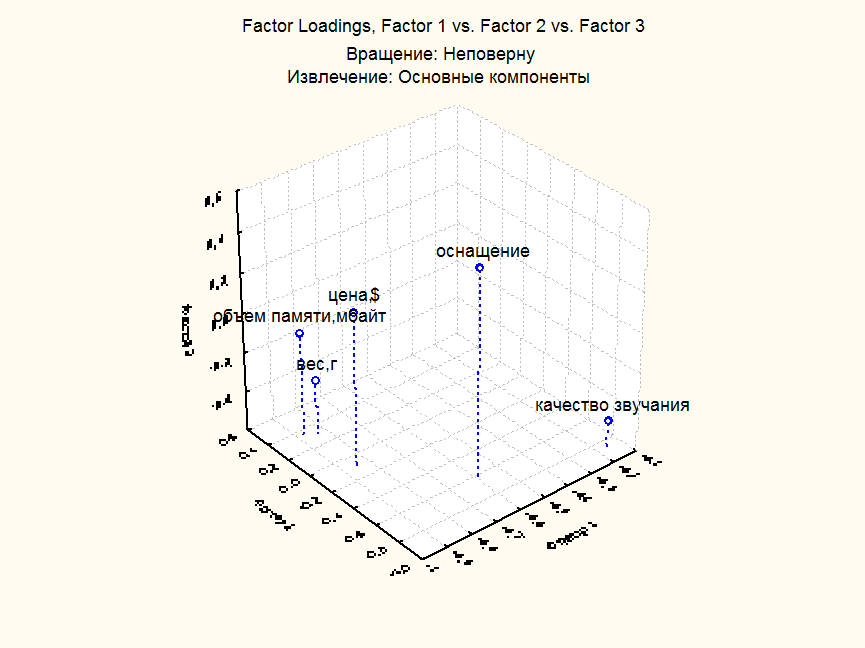
Очевидно, что при переходе к центроидному методу объем переносимой информации уменьшается, а факторы по-прежнему отражают ценовой показатель, внешние и технические характеристики, но с потерей информации.