Поиск образов, Терминология в поиске образов (Лабораторная работа № 8), страница 2

·  В  окне  редактора  ввести  следующие  2  строки:

 function z = my_fun(x)

z = x(1)^2 - 2*x(1)*x(2) + 6*x(1) + x(2)^2 - 6*x(2);

·  Сохранить  М-файл  как  my_fun.m.

В  выделенные  поля  «Целевая функция»  и  «Начальная  точка»  вводятся,  соответственно,  название  файла  и  координаты  начальной точки.

3. Ограничения

Ниже  первых двух строк  исходной панели  имеется  область  для установки  ограничений задачи,  которые  состоят  из:

·  Линейные  неравенства  -  Для  ограничения  вида  Ax ≤ b  ввести

- матрицу  А  в  поле  А=;

-  вектор b  в  поле  b=.

·  Линейные уравнения   - Для  ограничения  вида  Aeqx = beq ввести

-  матрицу  Aeq   в  поле  Aeq =;

-  ввести   вектор  beq   в  поле  beq =.

Границы  -  Для  ограничений  в  виде  границ   lb ≤ x  и  x ≤ ub  ввести

     -  вектор lb   для  нижней  границы  в поле  Lower = ;

     -  вектор ub   в  поле   Upper = .

Если в задаче  отсутствуют  некоторые  ограничения, то  соответствующие  поля  остаются  незаполненными.

3.  Запуск  алгоритма  поиска  образов

Для  запуска  алгоритма  нажать  клавишу  Start  в  панели   Run solver  (Запуск  решателя). После  этого:

     -  поле  Current iteration   (Текущая  итерация)  отображает  номер  текущей  итерации;

      - в  поле  Status and results   (Состояние  и  результаты)  появляется  сообщение  «Pattern search running»  (Выполнение  поиска  образа).

При  окончании  процесса поиска  в  поле  Status and results   (Состояние  и  результаты)  появляются  следующие  сообщения:

-  «Pattern search terminated»  (Поиск  образа завершен);

-  Значение  целевой функции  в  конечной  точке;

-   Основание  остановки  алгоритма;

-  Координаты  конечной  точки.

На  рис.4  показано  окно  с  итоговой  информацией.

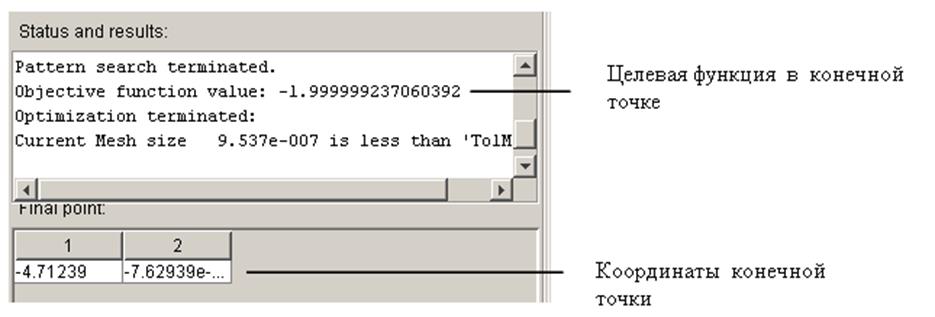
Рис.4. Итоговая   информация после  завершения алгоритма

4.  Пример задачи с  ограничениями

Здесь  рассмотрим  пример  выполнения  поиска  образа  с  ограничениями. Необходимо  найти  минимум  функции:

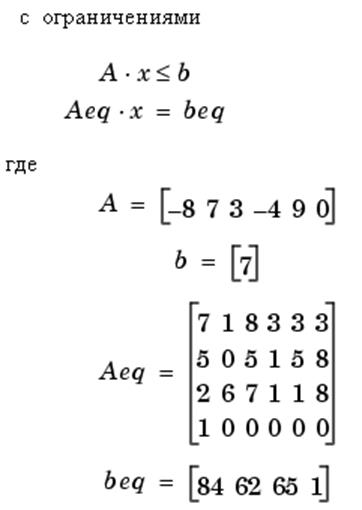
Для  выполнения  поиска  образа  в этом  примере  сначала  наберем  psearchtool  в  командном  окне.  Затем  в поле  целевой  функции  введем  @lincontest7  как М-файл, вычисляющий целевую  функцию для  этого  примера.  Вследствие того,  что  матрицы и вектора,  определяющие  начальную   точку,  достаточно  велики,  удобнее вначале   ввести их  значения  как  переменные  в  рабочее  пространство  MATLAB,  а  далее  ввести  имена  переменных  в  панель  Pattern Search. 

Таким  образом,  введем  в  командное  окно  следующие  5  строк:

x0 = [2 1 0 9 1 0];

Aineq = [-8 7 3 -4 9 0];

bineq = [7];

Aeq = [7 1 8 3 3 3; 5 0 5 1 5 8; 2 6 7 1 1 8; 1 0 0 0 0 0];

beq = [84 62 65 1]

Затем  в  соответствующие  поля  панели  Pattern Search введем:

-  Начальное значение:  x0;

-  Линейные  неравенства:  A =  Aineq  и   b =  bineq;

-  Линейные  уравнения:  Aeq =  Aeq  и   beq =  beq.

На  рис.5  показана  часть панели  с  введенными  данными.

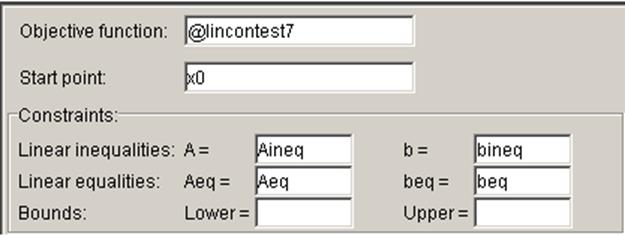
Рис.5. Панель  поиска  образа  после  ввода  данных

          После  этого  нажать  кнопку  Start для запуска  алгоритма.  При  завершении  поиска  результаты отобразятся  в  поле  Status and results,  как  приведено  на  рис.6.

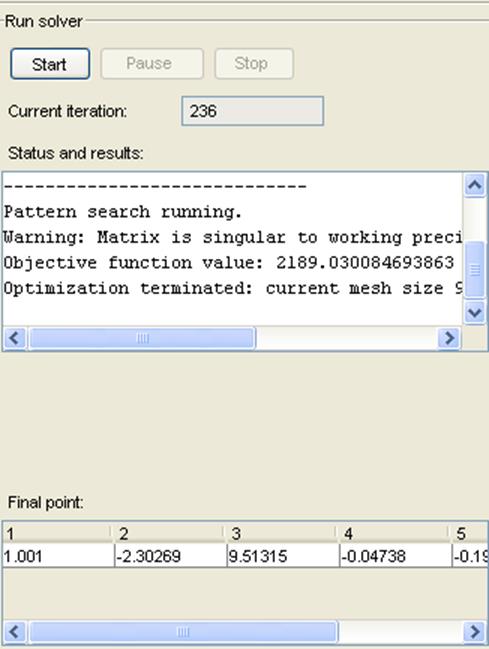
Рис.6. Результат  расчета

5.  Пауза  и  остановка  алгоритма

При  выполнении  алгоритма  можно  нажать  клавишу  Pause  (Пауза)  для  временной  остановки  алгоритма.  Для  повторного  запуска  алгоритма  с  момента  остановки  нужно  нажать   клавишу   Resume  (Перезапуск).

Для  остановки  алгоритма  нажать  клавишу  Stop.  В  поле  Status and results (Состояние  и  результаты)  отображается  значение  целевой функции текущей  точки  в  момент  остановки.