Оптимизация технологических факторов молочного охладителя ОМ-1

ЛАБОРАТОРНАЯ РАБОТА № 19

Тема: «ОПТИМИЗАЦИЯ ТЕХНОЛОГИЧЕСКИХ ФАКТОРОВ МОЛОЧНОГО ОХЛАДИТЕЛЯ ОМ-1»

Цель работы: Определить область оптимальных технологических режимов молочного охладителя.

НЕОБХОДИМОЕ ОБОРУДОВАНИЕ:

1. Охладитель молока ОМ-1.

2. Термометры (от 0°…100°С).

3. Мерные сосуды.

4. Секундомер.

СОДЕРЖАНИЕ РАБОТЫ

В экспериментах лабораторной работы приняты два основных технологических факторов-подача охлаждающей воды В и подача молока М, соотношение которых характеризуется коэффициентом кратности подачи воды:

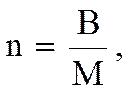
где  В - подача охлаждающей воды, кг/с;

М - подача молока, кг/с.

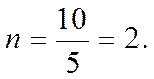
В качестве критерия оптимизации при оценке эффективности молочного охладителя удобно принять средний коэффициент теплопередачи:

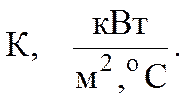
         Оптимальное сочетание факторов В и М необходимо определить с помощью теории планирования эксперимента методом крутого восхождения по поверхности откликов (метод Бокса-Уилсона), который предусматривает варьирование факторов на двух уровнях (верхнем +1 и нижнем -1).

Процедура крутого восхождения предусматривает назначение уровней варьирования факторов, составление плана эксперимента, реализацию плана, расчета коэффициентов регрессии, статистическую оценку результатов опытов и анализ математической модели.

Поскольку в нашем случае выбрано два фактора, то целесообразно реализовать полный факторный эксперимент типа 2²=4.

После реализации матрицы плана рассчитывают коэффициенты регрессии и получают математическую модель в виде неполного квадратичного полинома:

    .                                (1)

С целью сокращения времени на выполнение опытов рекомендуется каждую строку плана реализовать в однократной повторности, а одну из них, например, четвертую в трехкратной повторности (для оценки дисперсии ошибок) коэффициенты регрессии полинома рассчитываются по формулам (факторы в нормированном виде):

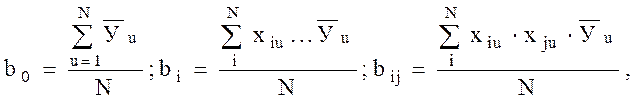
где N     - число строк матрицы плана, N = 4;

У_u - значение критерия оптимизации в u-ой строке;

x_iu - матрицы плана;

x_iu - значение i-го фактора в u-ой строке плана (u = 1...N).

После расчета коэффициентов регрессии проверяется адекватность модели по критерию Фишера (F - критерий):

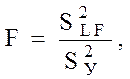
где  - дисперсия неадекватности.

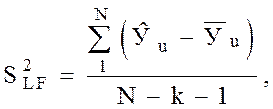
где  - расчетное значение критерия оптимизации по формуле (1) в u-ой строке плана;

k    - число факторов, k = 2;

 - дисперсия ошибок опыта

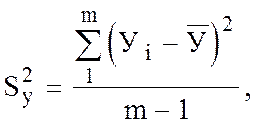
У_i - значения критерия оптимизации в i-ой параллельном опыте;

 - среднее значение критерия оптимизации для строки, которая была реализована несколько раз;

m - число параллельных опытов.

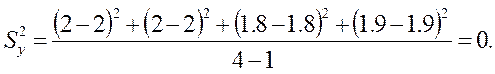
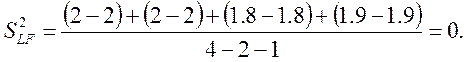
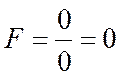
Вывод: Модель адекватна так как расчетное значение F-критерия меньше (F табл.).

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Перед началом опытов:

1. Снять размеры элементов секции охладителя и определить площадь поверхности охлаждения F, м² по формуле:

F = 1,2 L ^. H ^. Z;

где L - длина пластины охладителя, L = 0,6 м;

Н - ширина пластины охладителя, Н = 0,07 м;

Z - число пластин в охладителе, Z = 41.

F = 1,2^. 0.6 ^. 0.07^. 41=2.07м²

2. Экспериментально-теоретическое определение среднего коэффициента теплопередачи на каждом режиме производится в таком порядке.

В период охлаждения фиксируются показания термометров, установленных на прямом и обратном водопроводах секции в молокоприемнике и молокосборнике, а также в начале и конце линии охлаждающей воды.

2.1. Подача установки, кг/ч:

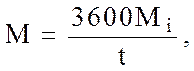
где M_i - количество охлажденного молока за время опыта;

t     - продолжительность опыта, с.

Таблица 2 - Результаты опытов

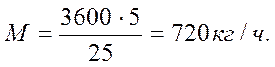
№№ строки	Время опыта, с		М1	В1	tначм,	tконм,	tначв,	tконв,
плана	В	М	кг	кг	оС	оС	оС	оС
1	47	25	5	10	41	23	21	23
2	80	44	5	10		30		28
3	36	45	5	10		25		29
4	46	23	5	10		27		30
5	46	24	5	10		27		33
6	53	18	5	10		27		34

2.2 Расход воды водяной секцией, кг/ч:

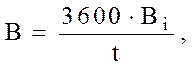
где B_i - количество воды за время t опыта, кг.

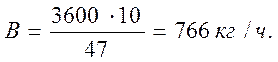
2.3. Логарифмическая разность температур

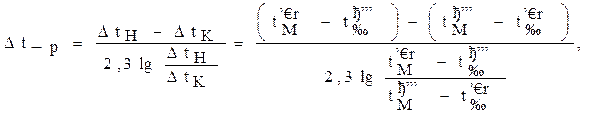
где Dt_н - разность температуры между начальной температурой молока и конечной температурой воды;

Dt_к - разность температур между конечной температурой молока и начальной температурой воды.

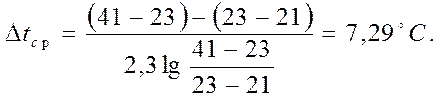
2.4. Средний коэффициент теплопередачи, кВт/(м² с):

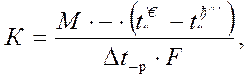
где М - массовый расход молока, кг/с;

с - теплоемкость молока, С= 3,9356 кДж/(кг с).

      Поскольку в опытах вместо молока используется вода, то принято

С= 4,19 кДж (кг с)

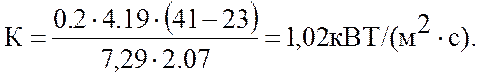
Данные расчета сводим в таблицу.

Таблица 3-Расчетные данные

№	М	В	Dtк	К
1	720	766	7,29	1,02
2	409	450	10,89	0,26
3	400	1000	7,29	1,07
4	783	783	8,26	0,87

Таблица 1 - Матрица планирования и результаты расчетов

	Факторы		Экспериментальная оценка критерия оптимизации
Обозначения	Пода-ча  воды В, кг/с	Подача молока М, кг/с
	Х1	Х2
Верхний уровень +1	0,53	0,2
Нижний уровень -1	0,22	0,09
План опытов: 1                        2                        3                        4	+ - + -	+ - - +	1,02		0.8
			0,26		1
			1,07		1.5
			0,87		1.7
Оценки коэффициентов регрессии	во	в1		в2		в12
	0.798	0.267		0.137		-0.139

3. Провести анализ модели (1) графоаналитическим методом.

Для чего необходимо построить двумерные сечения:

3.1. Задаваясь значениями Х₁ (Х₂) равными -1; -0,5; 0; 0,5 ; 1 .

В координатах Х₁ Х₂ по полученным точкам построить пять линий равного выхода (рисунок 1).

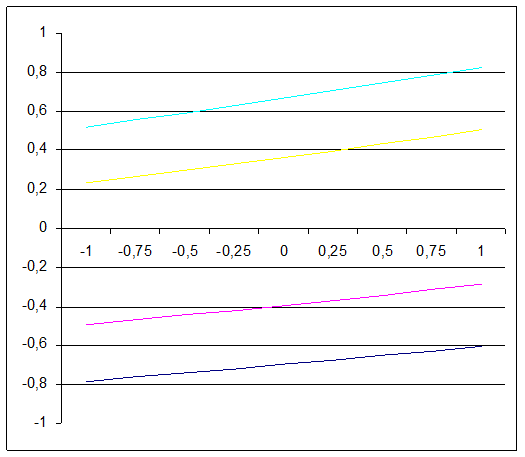
Рисунок1 -  Двумерное сечение поверхности отклика

Анализируя линии равного выхода, определить оптимальные значения: факторов Х₁ ^опт. и Х₂ ^опт.. Оптимальные значения факторов подставить в (1) и найти значение У ^опт. сравнить его величину с лучшими точками по данным эксперимента и сделать вывод о степени увеличения критерия оптимизации в оптимальной точке.

У=0.798+0.267*0.5+0.137*0.6-0.139*0.5*0.6=0.972.       

3.2. Оптимальные значения Х₁ ^опт. =0.5 и Х₂ ^опт. =0.6 раскодировать, то есть сделать их именованными по формуле:

Х1=0.5*0.155=0.0775кг/с.

Х2=0.6*0.055=0.033кг/с.

где Х - именованное значение i-го фактора, кг/с;

Х_i - нормированное значение i-го фактора (безразмерная величина);

Е_i - шаг варьирования фактора, кг/с:

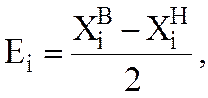
где 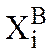    - именованное значение фактора на верхнем уровне (+1);

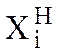- именованное значение фактора на нижнем уровне (-1).

Например, уровни подачи воды были  = 0,53 кг/с; 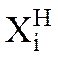  = 0,22 кг/с.

Отсюда шаг

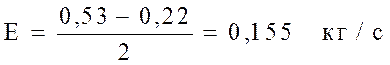
Вывод: Оптимальные значения Х1=0.0775кг/с, Х2=0.033кг/с, У=0.972