Конспект лекций по курсу: «Основы построения Земных станций и бортовых ретрансляторов». Часть 4: "Спутниковый транспондер (бортовой ретранслятор)" (Устройства ограничения в транспондерах. Нелинейные бортовые усилители), страница 2

Таким образом рис. 4.17 позволяет оценить отношение коэффициентов ослабления несущей и шума, заданных в (4.5.12). Это означает, что сами по себе коэффициенты ослабления зависят от величины входного отношения сигнал/шум CNR_i. Для определения величин ослабления воспользуемся формулами (4.5.6) и (4.5.11), из которых получим

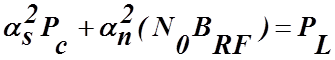                                    .                            (4.5.14)

Из формулы (4.5.13) находим

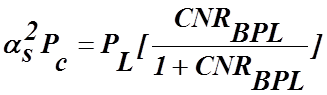                                                                  (4.5.15а)

и определяем

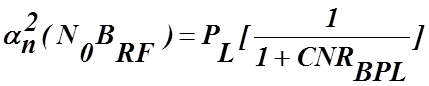                           .                          (4.5.15б)

Исследуем влияние ограничителя, которое проявляется в спектральной области. Для этого рассмотрим несущее колебание, представленное квадратурными компонентами на выходе фильтра (4.3.8) и поступающее на вход ограничителя в виде

.         (4.5.16)

Выход полосового ограничителя описывается выражением (4.5.2), где

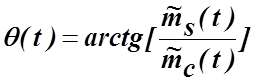.                              (4.5.17)

Представив (4.5.2) с помощью квадратурных составляющих

                                    (4.5.18)

получим

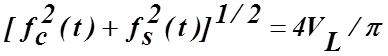                                (4.5.19)

и

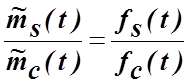                                            .                                      (4.5.20)

Для решения этих уравнений требуется, чтобы

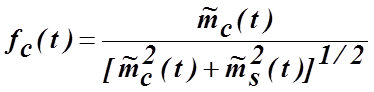                                    ,                        (4.5.21а)

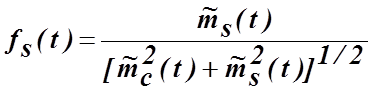                                    .                        (4.5.21б)

Видно, что полосовой ограничитель преобразует квадратурные компоненты   и  несущей в новые компоненты, представленные в (4.5.21). В частности, ограничитель порождает связь между QPSK компонентами, так как частоты  и  зависят от обоих потоков данных. Например, при офсетном формате QPSK, если функция  меняет знак бита в течение длительности бита , то  также меняет знак бита. Однако, поскольку функция  пересекает нулевой уровень в течении длительности бита, величина f(t) в (4.5.21а) должна принимать значение 1 в течение продолжительности бита. Следовательно, f(t) создает всплески в форме сигнала, соответствующие переходам квадратурных компонент битов, то есть соответствующие центру бита (см. рис. 4.18).

Спектр несущего колебания после ограничения y(t) в (4.5.18) может быть рассчитан в соответствии с (4.3.2) как

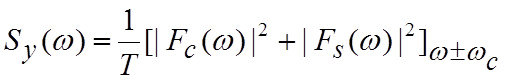,                  (4.5.22)

где F_c(ω) и F_s(ω) – спектры f_c(t) и f_s(t) в (4.5.21), соответственно. В общем случае данные спектры трудно рассчитать, так как они включают отношения временных функций и двух различных последовательностей данных. Для расчетов спектров обычно используют численные методы.

 

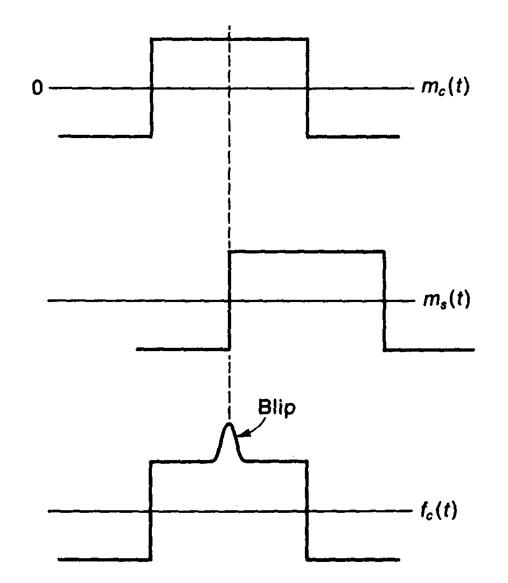Рис. 4.18. Появление всплеска (blip) при модуляции QPSK.

 На рис. 4.19 показаны результаты расчетов спектров в соответствии с формулой (4.5.22).

 

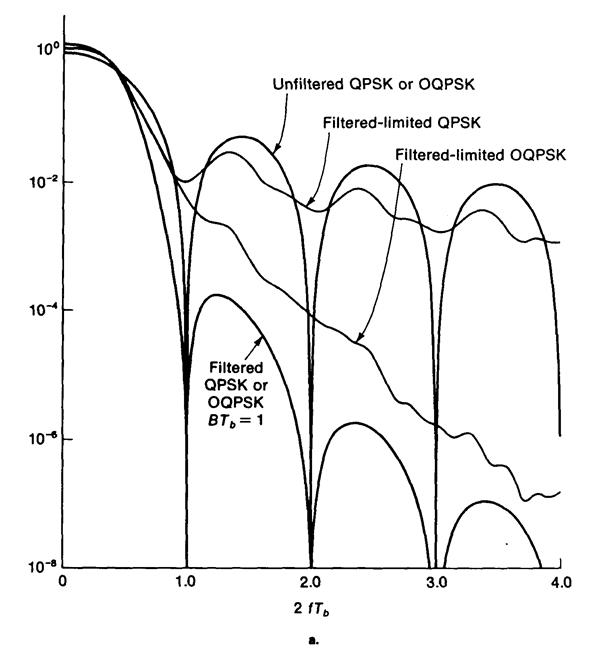Рис. 4.19а. Спектр после полосовой фильтрации, соответствующий жесткому ограничению: QPSK и ОQPSK.

 

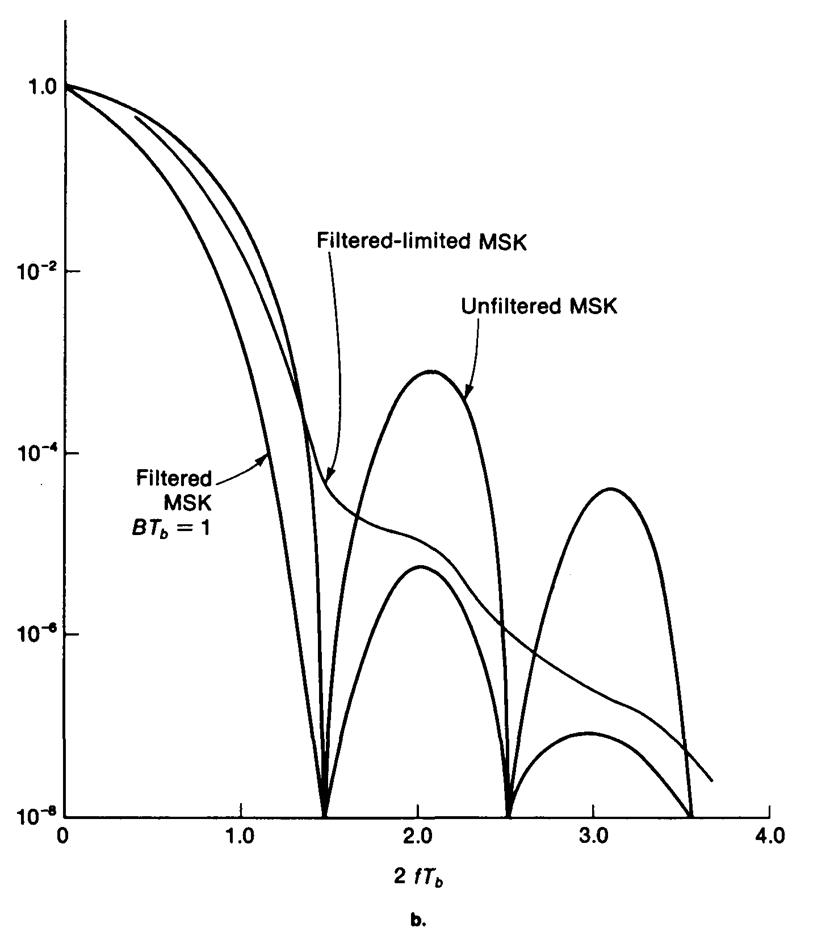         Рис. 4.19б. Спектр после полосовой фильтрации, соответствующий жесткому ограничению: МSK.

Из приведенных рисунков видно, что в то время как фильтрация уменьшает уровень боковых лепестков («хвостов») спектральной функции, процедура жесткого ограничения сохраняет «хвосты» в спектре. Поэтому в результате процедуры ограничения несущего колебания его спектр выходит за пределы выше отмеченной спектральной маски.

Анализ рис. 4.19 показывает, что при стандартной модуляции QPSK уровень спектральных «хвостов» выше по сравнению с системами, использующими ОQPSK и МSK.

4.6. Нелинейные бортовые усилители

Обычно на борту спутника используют усилители мощности на лампе бегущей волны (ЛБВ). ЛБВ были первоначально разработаны только для усиления сигналов постоянной амплитуды. Вариации амплитуды колебаний на входе ЛБВ порождают дополнительную непреднамеренную фазовую модуляцию, влияние которой проявляется в виде фазовой помехи в усиливаемом фазомодулированном колебании.

Если амплитуда колебания на входе ЛБВ увеличивается, то амплитуда на выходе ЛБВ также увеличивается до уровня, ограниченного насыщением. Зависимость выходной мощности ЛБВ от мощности на входе приведена на рис. 4.20а.

 

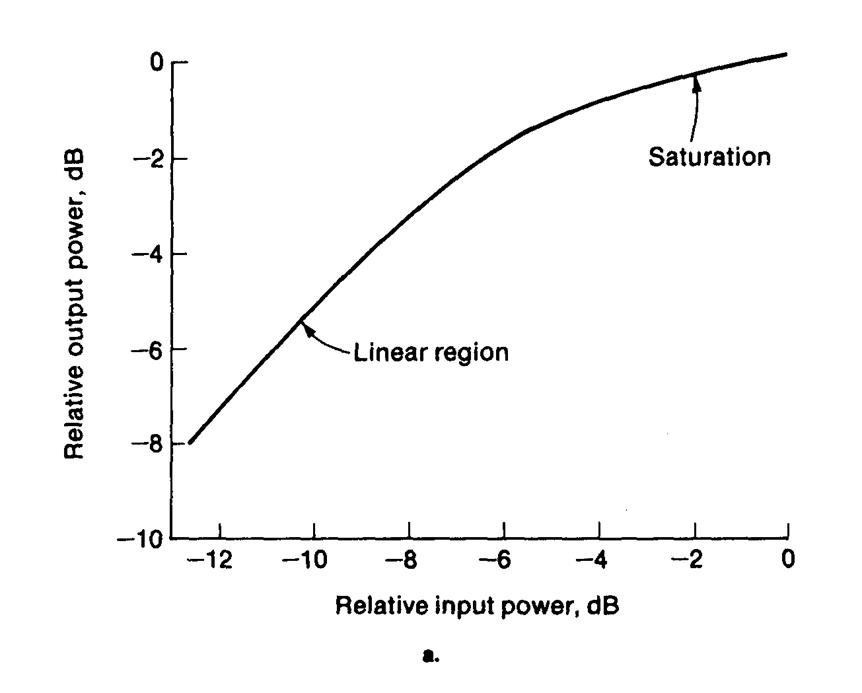Рис. 4.20а. Зависимость выходной мощности от входной мощности ЛБВ.

 

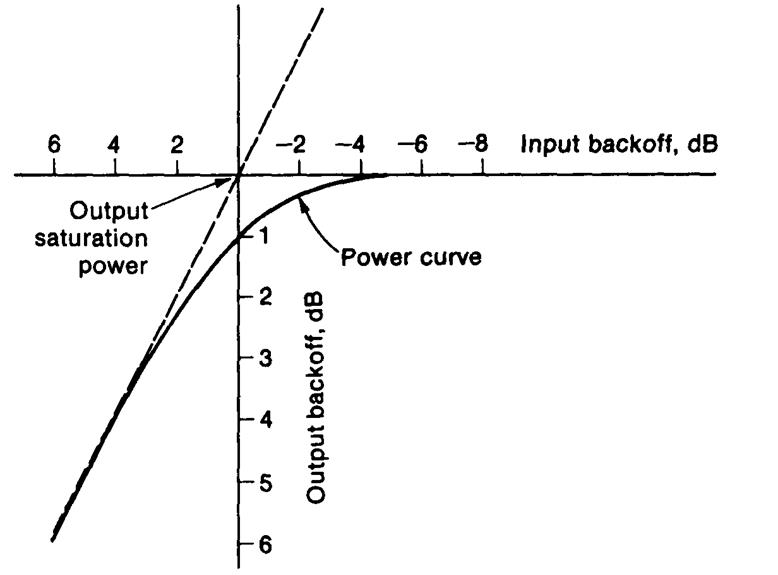Рис. 4.20б. Характеристика потерь мощности при насыщении ЛБВ.