Структурные и частотные методы исследования линейных САР, страница 2

3)  Определение устойчивости РС с помощью критерия Михайлова.

0	0	0
0,001	-0,00002	0,001
0,002	-0,00008	0,001999
0,003	-0,00018	0,002997
0,004	-0,00032	0,003994
0,005	-0,0005	0,004988
0,006	-0,00072	0,005979
0,007	-0,00098	0,006967
0,008	-0,00128	0,007951
0,009	-0,00162	0,00893
0,01	-0,002	0,009904
0,0104	-0,0021632	0,010292
0,015	-0,0045	0,014676
0,02	-0,008	0,019232
0,03	-0,018	0,027408
0,05	-0,05	0,038
0,07	-0,098	0,037072
0,09	-0,162	0,020016
0,1	-0,2	0,004

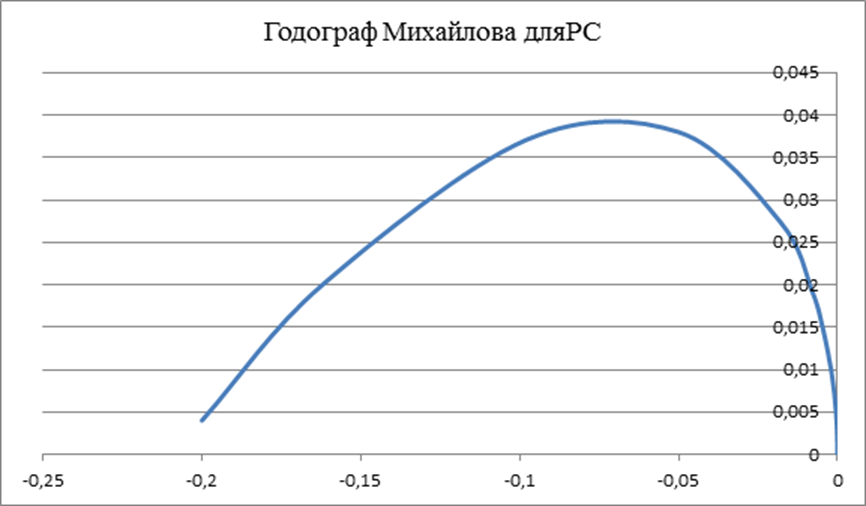
САУ в РС нейтральна, т.к. годограф проходит через начало координат.

7.  Определение устойчивости замкнутой САР с помощью критериев

Гурвица, Михайлова, Найквиста, метода перемежаемости корней,

логарифмического критерия Найквиста.

1)  Определение устойчивости ЗС с помощью критерия Гурвица:

B(P)=0    

n=3

      

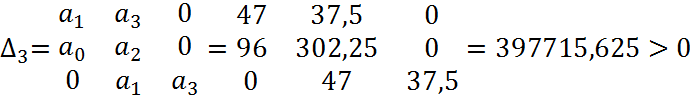
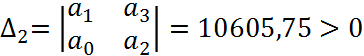
Т.к. все условия выполняются, следовательно, САУ в ЗС устойчива.

2)  Определение устойчивости ЗС с помощью метода перемежаемости корней:

; ;

;

0<0,89<1,77

Следовательно, САУ в ЗС устойчива.

3)  Определение устойчивости ЗС с помощью критерия Михайлова.

0	0	0
0,1	-0,00002	0,001
0,2	-0,00008	0,001999
0,3	-0,00018	0,002997
0,4	-0,00032	0,003994
0,5	-0,0005	0,004988
0,6	-0,00072	0,005979
0,7	-0,00098	0,006967
0,89	-0,00128	0,007951
0,9	-0,00162	0,00893
1	-0,002	0,009904
1,2	-0,0021632	0,010292
1,4	-0,0045	0,014676
1,5	-0,008	0,019232
1,6	-0,018	0,027408
1,77	-0,05	0,038
1,8	-0,098	0,037072
1,9	-0,162	0,020016
2	-0,2	0,004

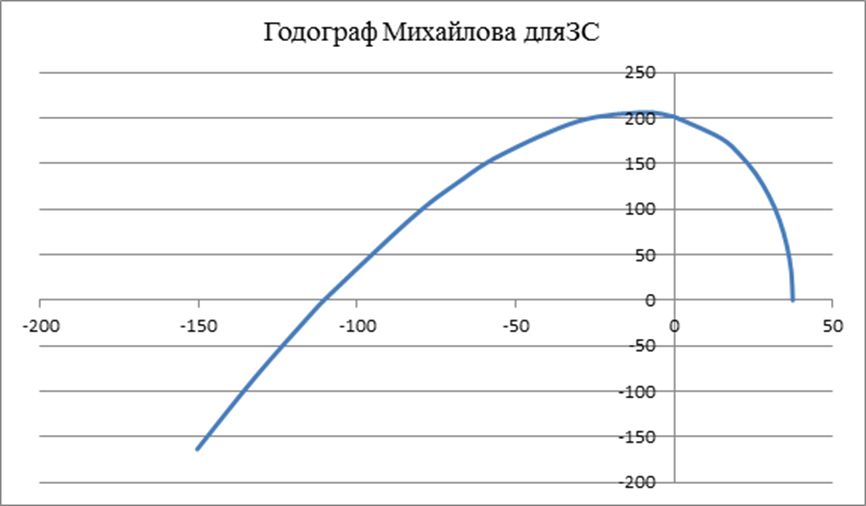
САУ в ЗС устойчива.

4)  Определение устойчивости замкнутой системы с помощью критерия Найквиста.

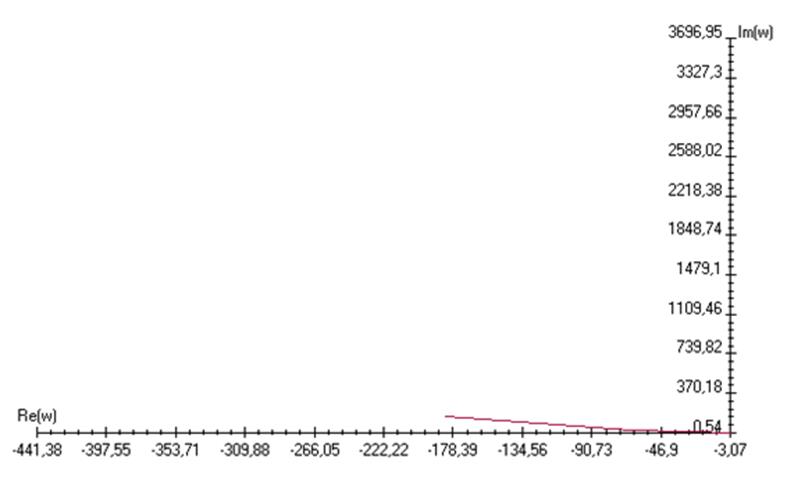
АФЧХ разомкнутой САР

САР в замкнутом состоянии устойчива.

5)  Определение устойчивости замкнутой системы с помощью логарифмического критерия Найквиста.

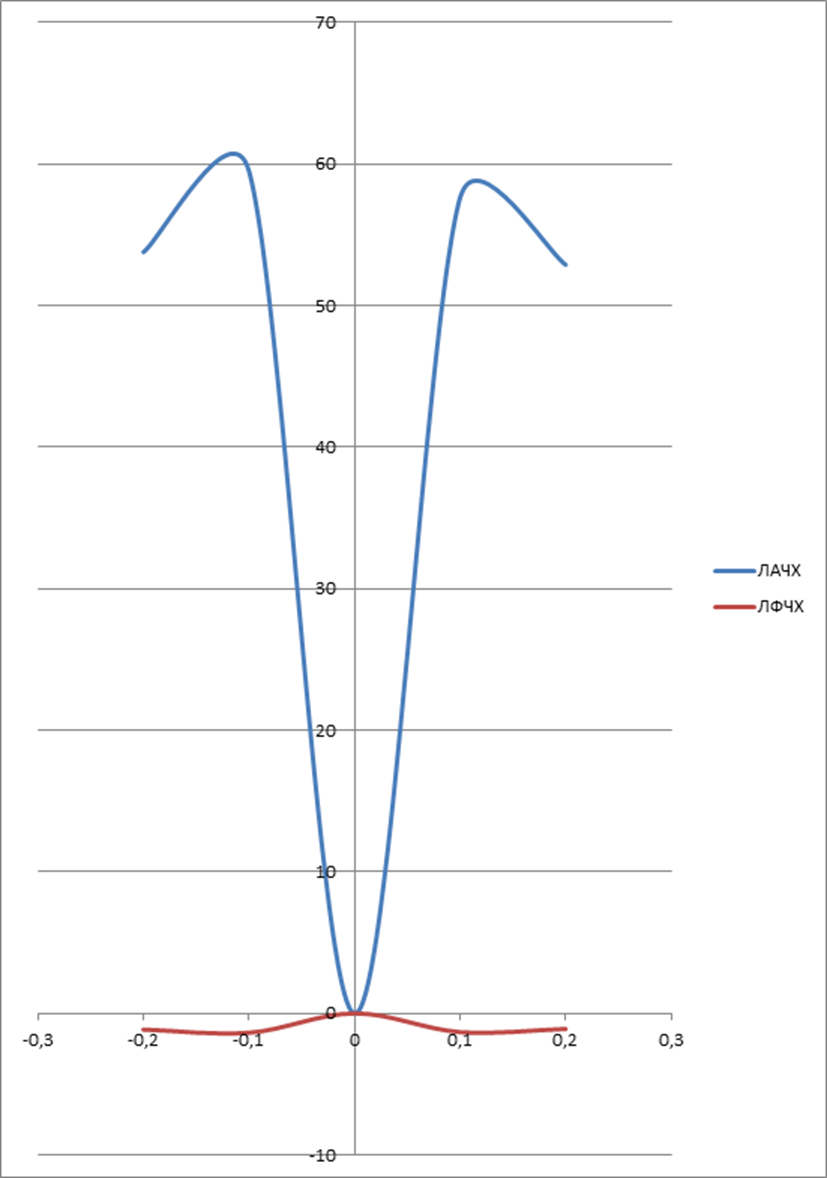
САР в замкнутом состоянии устойчива.

6)  Определение величины запаса устойчивости ЗС по фазе:

8.  Оценка качества переходного процесса в замкнутой системе по

интегральному критерию.

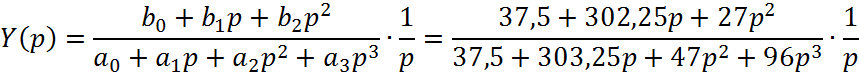
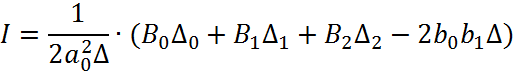
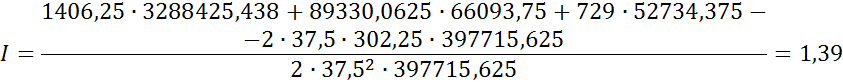
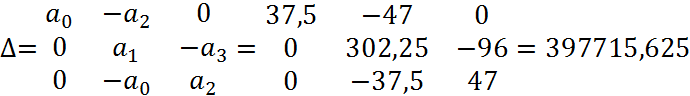
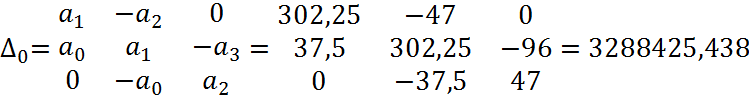
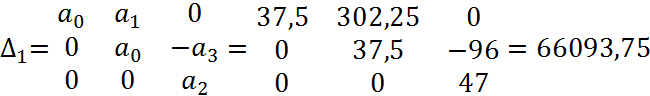
9.  Анализ результатов исследования САР.

Ознакомилась, изучила и применила на практике структурные и частотные методы исследования линейных САР.

С помощью различных критериев определила, что система в разомкнутом состоянии неустойчива, а в замкнутом устойчива.

Результаты оценки качества переходного процесса в замкнутой САР показали, что качество переходного процесса достаточно высоко, т.к. I=1,39, что довольно невелико.

Список литературы.

1.  Теория автоматического управления. Анализ линейных систем. Ю.А. Михайлов. – Братск: 2009. – 34 с.

2.  Теория автоматического управления: Учеб. Для вузов/С.Е. Душин, Н.С. Зотов, Д.Х. Имаев и др.; Под ред. В.Б. Яковлева. – 2-е изд., перераб. – М.: Высш. Шк., 2005. – 567 с.

3.  Востриков А.С., Францезова Г.А. Теория автоматического управления: Учеб. Пособие для вузов. – М.: Высш. шк., 2006. – 365 с.

4.  Теория автоматического управления. Часть I. Линейные системы: Методические указания / Т.Н. Буштрук, Н.Н. Дубынина. – Братск: БрИИ, 1988. – 74 с.

5.  Расчет автоматических систем. Под ред. А. В. Фатеева. Учеб. Пособие для вузов. – М.: Высш. шк., 1973. – 366с.