Исследование тепловой инерции термометров (Теоретические сведения, описание и порядок выполнения лабораторной работы № 2)

Министерство образования Российской Федерации

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ

ГИДРОМЕТЕОРОЛОГИЧЕСКИЙ

УНИВЕРСИТЕТ

Кафедра

экспериментальной физики

атмосферы

ЛАБОРАТОРНАЯ  РАБОТА  № 2

по дисциплине

“Методы и средства гидрометеорологических измерений”.

ИССЛЕДОВАНИЕ ТЕПЛОВОЙ ИНЕРЦИИ ТЕРМОМЕТРОВ

Направление - Гидрометеорология

Специальность - Метеорология

 

Санкт - Петербург

2001

УДК 551. 508

Лабораторная работа № 2. Исследование тепловой инерции термометров.  По дисциплине “Методы и средства гидрометеорологических измерении”. – С.-Петербург.: РГГМУ, 2001, 17 с.

          Лабораторная работа составлена на основе типовой программы дисциплины, читаемой студентам метеорологического факультета.

          Работа содержит теоретические сведения, описание и порядок работы с используемыми приборами и перечень операций, выполняемых студентами. В приложении приводится метод наименьших квадратов для расчета коэффициента инерции термометра.

          Издание дополнено в 2004 году для размещения в сети Интернет.

Составители: Редактор:

Григоров Н.О., доцент Белоцерковский А.В., профессор Кузнецов А.Д., профессор

Ó  Российский государственный гидрометеорологический университет (РГГМУ), 1999.

Цель работы - определить коэффициенты тепловой инерции термометров в различных условиях. Исследовать зависимость коэффициента тепловой инерции термометра от скорости воздушного потока. Обработать полученную зависимость с помощью метода наименьших квадратов.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Реальные термометры, обладающие термометрическим телом, не в состоянии мгновенно воспринимать изменение температуры окружающей среды. Поскольку теплообмен между термометрическим телом (например, резервуаром термометра) и средой  происходит с конечной скоростью, требуется некоторое время для того, чтобы термометр показал изменившуюся температуру среды. Эта особенность получила название тепловой инерции термометра. Тепловой инерцией обладают все термометры, имеющие термометрическое тело - жидкостные, деформационные, резисторные и т.п. Бывают, однако, практически безинерционные термометры, например, акустические, радиационные, у которых нет термометрического тела. В таких термометрах их инерция обусловлена лишь запаздыванием регистрирующей части прибора - например, показывающей стрелки. Эта инерция обычно гораздо меньше тепловой. В данной работе исследуется только тепловая инерция.

          Основные уравнения, характеризующие тепловую инерцию термометра, приведены  в книге [1], а также в курсе лекций по данной дисциплине. При подготовке к работе студенты должны изучить раздел 2.1 книги [1] и содержание лекции №1 [2].

          Предположим, что термометр, имеющий температуру Т₀, внесен в среду, имеющую температуру Θ. При постоянной температуре среды термометр в дальнейшем будет показывать температуру, изменяющуюся о закону:

где Θ - температура окружающей среды,

      τ - время,

      λ - коэффициент тепловой инерции термометра.

Смысл величины λ ясен из уравнения (1) - коэффициент тепловой инерции термометра численно равен времени, в течение которого разность температур между термометром и средой уменьшается в е раз.

          Коэффициент λ зависит как от конструкции термометра, так и от свойств среды, в которой проводится измерение. Эта зависимость выражается формулой:

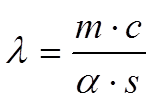где m - масса термометрического тела ,

       с - удельная теплоемкость вещества, из которого изготовлено термометрическое тело,

        α - коэффициент конвективного теплообмена между термометрическим телом и средой,

        s - площадь, через которую термометрическое тело обменивается теплом со средой. 

          В свою очередь, коэффициент конвективного теплообмена зависит от свойств среды:

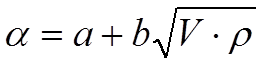где a, b - размерные константы,

      V - скорость движения воздуха,

      ρ - плотность среды.

          Таким образом, коэффициент инерции обратно пропорционален корню квадратному из произведения скорости потока на плотность среды.

          Следовательно, в более плотной среде, например, при измерении температуры воды, коэффициент инерции уменьшается.

          Если известна начальная разность температур T₀ - Θ, то для оценки коэффициента инерции термометра достаточно определить время τ*, в течение которого эта разность уменьшится в n раз. В самом деле, из уравнения (1) следует:

откуда

          Удобно взять n целым числом (n =2; 3 и т.п.). Это число n следует выбрать так, чтобы время τ* можно было бы легко определить по секундомеру (10-20 секунд).

          Задачей данной работы является определение коэффициента тепловой инерции нескольких стеклянных термометров при различных характеристиках окружающей среды и двух термометров сопротивления. В последнем случае работа выполняется с помощью двухкоординатного самописца, на котором записывается изменение температуры термометра во времени.