Измерения необычных волн и анализ таких измерений

В настоящее время хорошо известно, что высоты волн в океанах и морях могут достигать почти 30 метров. Например, в Баренцевом море 1 раз в 100 лет может встретиться волна высотой 24м. В Северном море аналогичная волна оценивается в 30 м. Большие волны встречаются не так уж редко и это не только никого не удивляет, но не представляют принципиальной опасности. Более важно, что среди экстремальных волн встречаются волны, которые не описаны в общепринятых нормативных документах, не объясняется в рамках существующих подходов. Однако о таких волнах известно по авариям судов и сооружений, из информации, предоставляемой судоводителями, а в последние годы и по измерениям с помощью различных приборов. Это, так называемые, необычные, ненормальные волны (в англоязычной литературе - freak или rogue waves) или даже волны-убийцы.

На сегодняшний день имеются измерения необычных волн и опубликованы некоторые данные анализа таких измерений. Ярким примером могут служить результаты измерений на Черном море. Здесь в районе Геленджика, начиная с 1996г., на глубине 85м., проводятся измерения волнения. За период измерений получено около 15 тыс. записей волнения и зарегистрировано около 4 миллионов волн. Только в декабре 2000г и ноябре 2001 во время штормов зафиксированы необычные волны. Информация о таких волнах приведена в таблице 1 [3]. Для сравнения в таблице приведены параметры необычной волны, зафиксированной в 1964 году в ходе I Атлантической экспедиции на судне «Айсберг».

Таблица1.

Параметры необычных волн зафиксированных на Черном море, а также параметры необычной волны, зафиксированной на волнограмме А-67 в 1964 году в ходе I Атлантической экспедиции на судне «Айсберг».

Дата	hmax	hmax/hs	hmax/h-	hmax/h+	c/hmax
16.12.2000	9.21	4.17	5.10	4.44	0.79
22.11.2001	10.32	3.91	4.86	2.84	0.86
24.11.2001	5.67	2.71	2.74	3.50	0.73
10.05.1964	15,66	2,39	2,64	5,13	0,70

Высоты волн подчинены закону Вейбулла 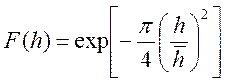 [4,5], а ординаты взволнованной поверхности – нормальному закону распределения [1,2]. Наличие необычной волны может сильно повлиять на результат при расчете плотности и функции распределения.

Характерной особенностью ветрового волнения на стадии его развития и затухания является то, что корреляционная функция имеет вид флуктуирующего процесса с «биениями», обусловленными групповой структурой волнения.

Из коррелограммы волнограммы А-67 видно, что коррелограмма слабо затухает. Флуктуационный период равен 15 с. Это говорит о том, что присутствует одна система волн.

Функция спектральной плотности является универсальной характеристикой, позволяющей описать разнообразие свойств волнения и решить многочисленные прикладные задачи. Поэтому очевидно стремление найти удобную аппроксимацию, позволяющую по минимальному числу параметров описать спектр волн. Существует огромное количество аппроксимаций, но наибольшее распространение получила модификация спектра, известная как спектр Пирсона-Московица. Она применима для  полностью  развитого  волнения. Полностью развитое волнение реализуется достаточно редко. Для ограниченных разгонов наиболее часто используется аппроксимация спектра вида JONSWAP (Joint North Sea Wave Project), впервые предложенная К. Хассельманном с соавторами на основании результатов эксперимента в Северном море. видно, что основное различие между спектрами заключается в значениях в окрестностях максимума, что определяется величиной γ. Высокочастотные области спектра (примерно для частот, в два раза превышающих частоту максимума) у обоих спектров совпадают и уменьшаются по зависимости, близкой к . При γ=1,0 спектр JONSWAP совпадает со спектром Пирсона-Московица.

Основная проблема практического использования спектра JONSWAP состоит в нахождении его параметров. Обычно принимают, что параметр σ = 0,07 для  и 0,09 для . Параметры α и γ зависят от скорости ветра и его разгона. В зависимости от того, по каким моментам спектра определяется период волн, соотношения между  или  и периодом T будут различны.

Для волнограммы А-67 функция спектральной плотности была посчитана через коррелограмму и аппроксимирована спектром вида JONSWAP (с параметрами γ = 4,5, α = 0,0078, = 0,073)