Текст программы.
Program;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
Edit1: TEdit;
Edit2: TEdit;
Edit3: TEdit;
Edit4: TEdit;
Edit5: TEdit;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel;
Edit6: TEdit;
Edit7: TEdit;
Label6: TLabel;
Label7: TLabel;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
procedure TForm1.Button1Click(Sender: TObject);
var
g:textfile;
dt,dx,h,w,U0,tt,f,coss,sinn:real;
a1,i,t,t0,n:integer;
U,V,Z,q:array [1..1000] of real;
Ug,Vg,Zg:array [1..1000] of TPoint;
a,a2:string[25];
begin
dt:=strtofloat(edit1.text);
dx:=strtofloat(edit2.Text);
H:=strtofloat(edit3.Text);
w:=strtofloat(edit4.Text);
U0:=strtofloat(edit5.Text);
t0:=strtoint(edit6.Text);
n:=strtoint(edit7.text);
for i:=1 to n do
begin
U[i]:=0;
V[i]:=0;
z[i]:=0;
end;
f:=1.4e-4;
coss:=cos(f*dt);
sinn:=sin(f*dt);
tt:=0;
for t:=1 to t0 do
begin
tt:=tt+dt;
U[1]:=U0*sin(w*tt);
for i:=2 to N do
begin
U[i]:=(U[i]*coss+(V[i]+(-9.81*(z[i]-z[i-1])/dx/f))*sinn);
V[i]:=(V[i]*coss-U[i]*sinn+(-9.81*(z[i]-z[i-1])/dx/f)*(coss-1));
end;
for i:=1 to n-1 do
z[i]:=z[i]-H*(U[i+1]-U[i])/dx*dt;
z[N]:=U[n]*sqrt(H/9.81);
for i:=1 to n do
begin
ug[i].y:=200-round(u[i]*10);
vg[i].y:=200-round(v[i]*10);
ug[i].x:=50+i*3;
Vg[i].x:=50+i*3;
zg[i].y:=200-round(z[i]*10);
zg[i].x:=50+i*3;
end;
with form1.Canvas do
begin
brush.Color:=clwhite;
rectangle(50,50,400,400);
pen.Color:=clred;
polyline(ug);
pen.Color:=clgreen;
polyline(Vg);
pen.Color:=clblue;
polyline(zg);
end;
if (t mod 10)=0
then
begin
a1:=(t mod 10)+t;
a2:=intToStr(a1);
a:='D:/KURS/res'+a2+'.dat';
Assignfile(g,a);
rewrite(g);
write(g,' i ',' U_m/c ',' V_m/c ',' Z_m');
writeln(g);
For i:=1 to n do
begin
q[i]:=i;
writeln(g,q[i]:9:0,U[i]:9:4,V[i]:9:4,z[i]:9:4);
end;
CloseFile(g);
end;
showmessage('qwerty');
end;
end;
end.
Задаваемые параметры:
dt=100c
dx=1000m
H=10m
W=1e-3, 1e-4, 1e-5
Uo=10m/c
to=1000
N=1000
Описание программы.
Представленная выше программа служит для расчета геострофического приспособления волновых колебаний уровня, а именно возмущения уровня, скоростей U, V. Данная программа состоит из следующих частей.
Первая часть это описание характеристик, присвоение им типов ( вещ.”real”, цел.”integer”, задание массивов array [1..1000] в том числе и графических и т.д.).
Следующая часть это задание исходных значений. Основные величины задаются из графического поля, но не все. Начальное значение возмущения, а также скоростей U и V задаются циклом в теле программы ( в начальный момент они равны 0).
Далее следует непосредственно расчетная часть, который состоит из нескольких циклов.
Общий по времени, этот цикл обедняет в себя следующие блоки. Блок с расчетными формулами представлен в виде цикла (именно в нем происходит расчет характеристик возмущения уровня, а так же скоростей в заданных точках. За конкретный момент времени. Для их расчета использовалась, конечно разностная схема. Скорость в нулевой точке меняется по синусоиде и рассчитывается по отдельной формуле.). Следующий блок графический. Он состоит из цикла формирующего графические массивы, а так же графической части, в которой рисуется график каждой величины, причем своего цвета. Завершает все это блок вывода в файл. Он формирует фай за каждой десятый момент времени, в который записывает четыре столбца значений ( номер точки I, U, V, Z). Имя файла присваивается в зависимости от момента времени, за который он формируется. Для того, чтобы можно было видеть результат за каждый момент времени в конце временного цикла выводиться сообщение, прерывающее программу до подтверждения.
Графическое представление полученных результатов.
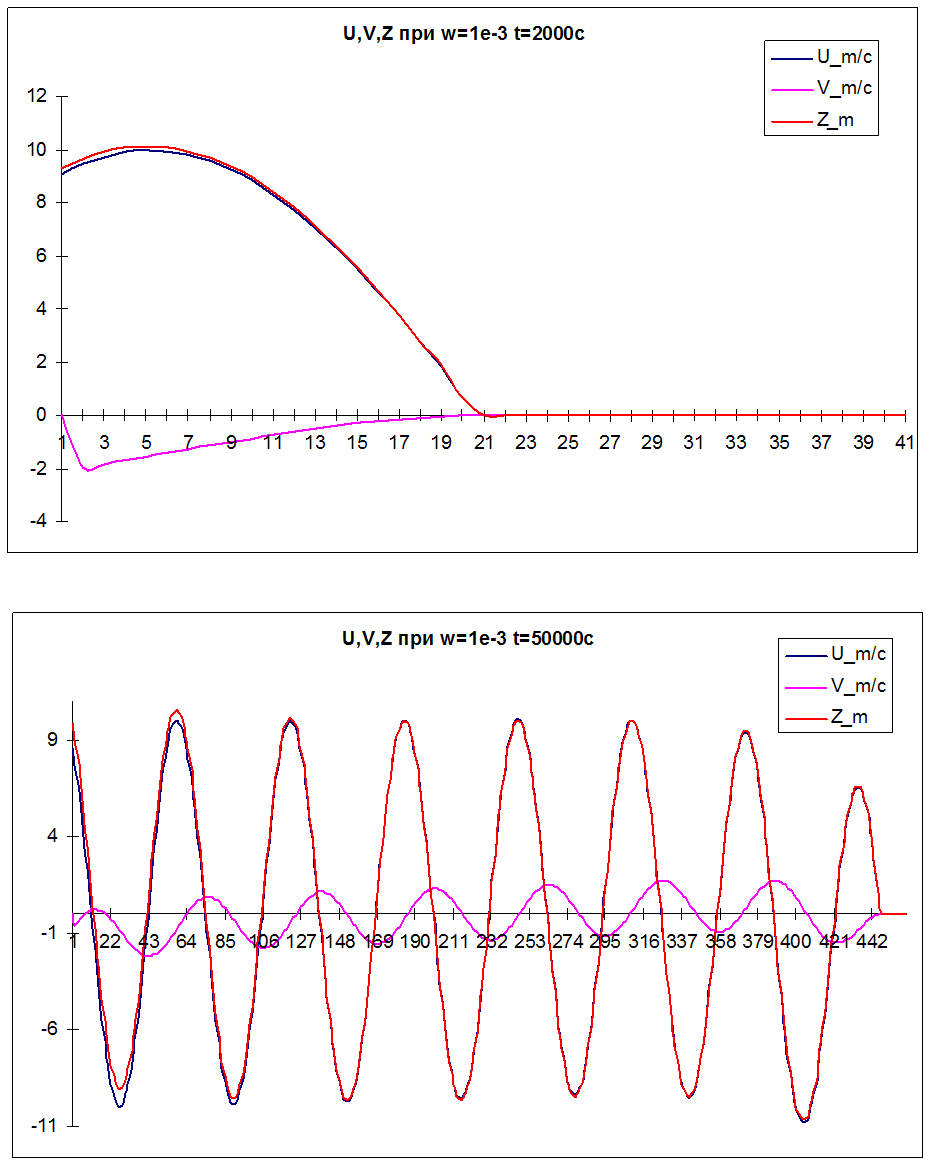
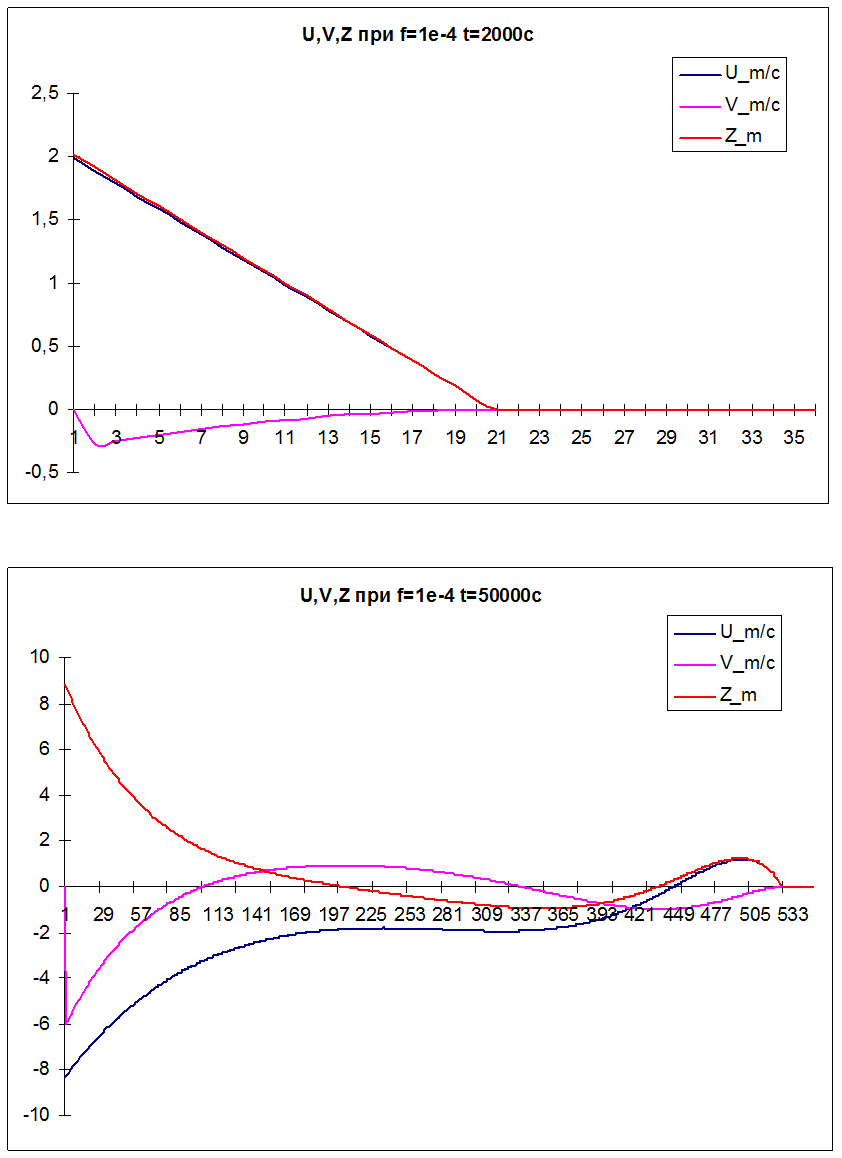
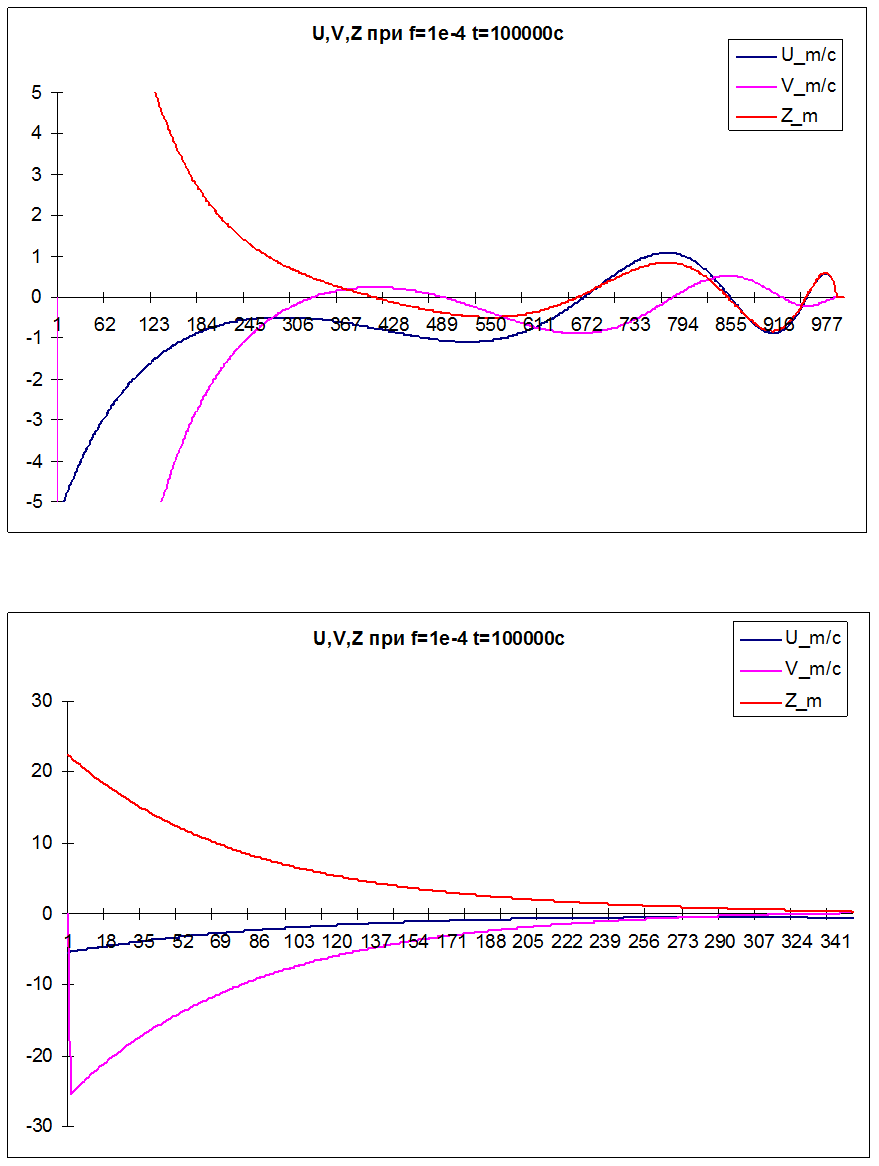
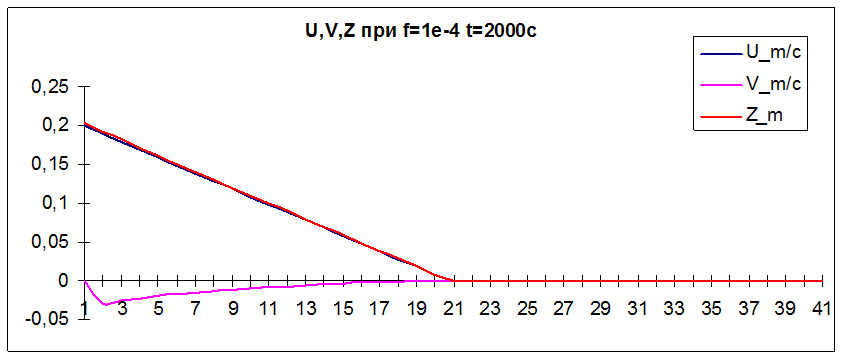
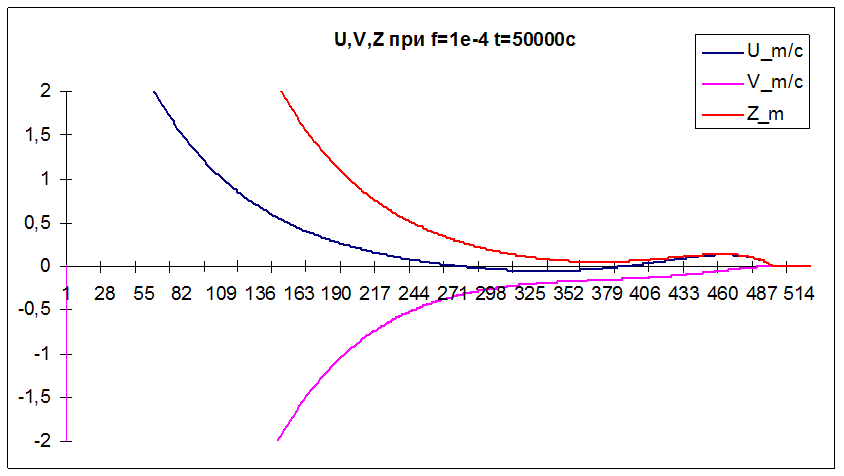
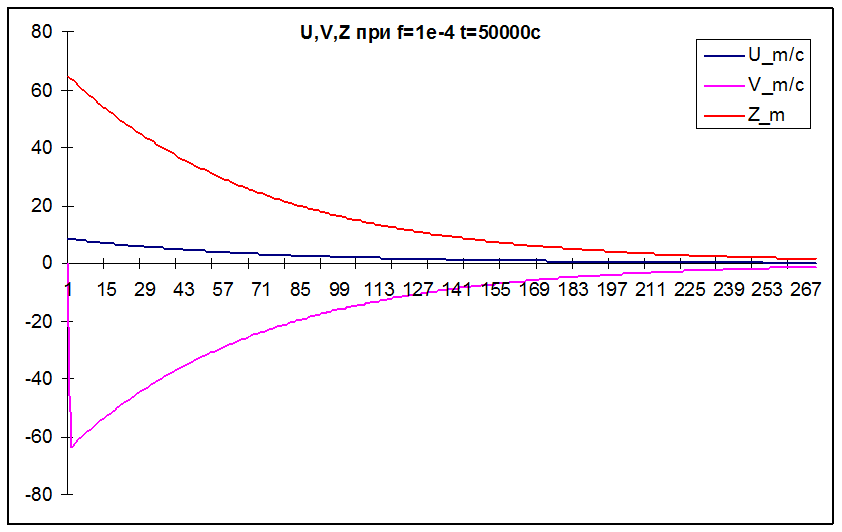
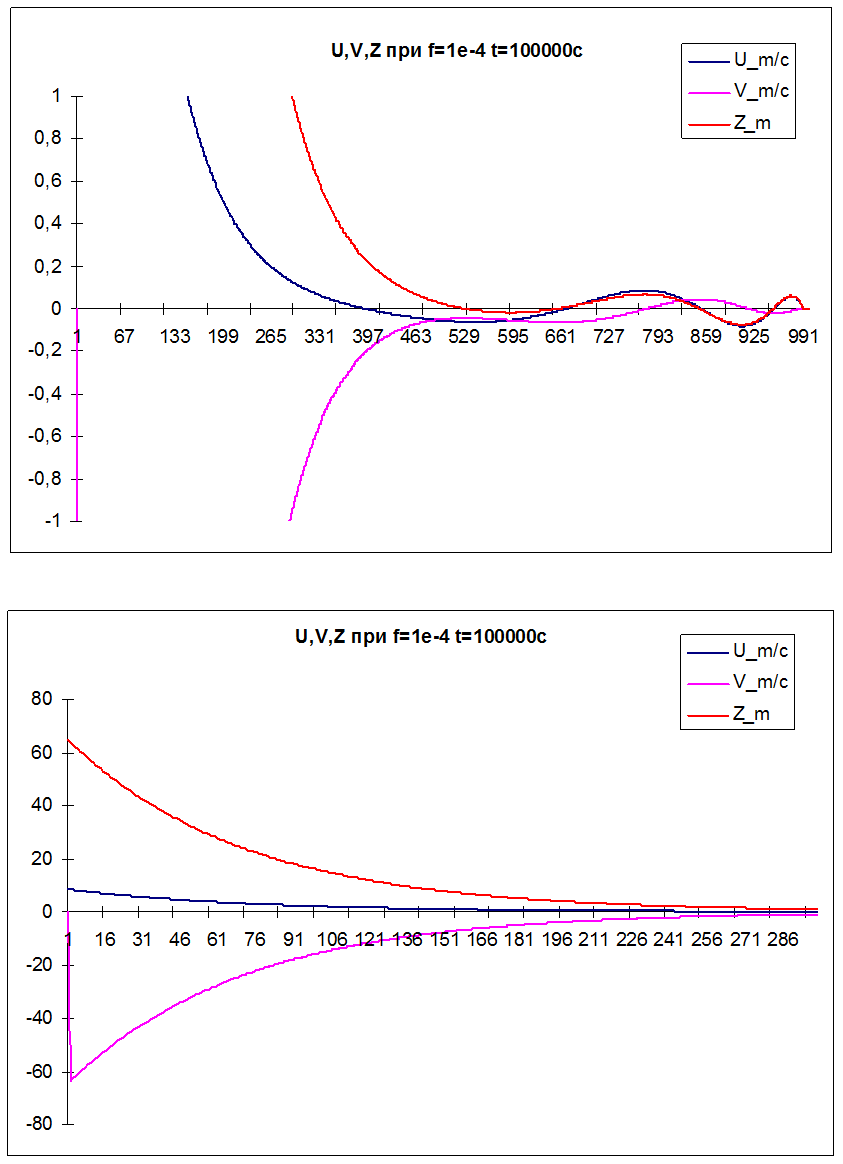
Теоретическая часть.
В данной курсовой работе рассматриваются волны мелкой воды, для которых характерно следующее дисперсионное соотношение:
где
есть квадрат горизонтального волнового числа. Волны с таким дисперсионным соотношением (k, l вещественные) называются « волнами Пуанкаре». Несмотря на то, что эти волны носят имя Пуанкаре, впервые они были рассмотрены Кельвином. В метеорологии их обычно называют просто гравитационными, подразумевая при этом, что они связаны с влиянием вращения. Из дисперсионного соотношения можно увидеть, что свойства волн зависят от соотношения между длинной волны и радиксом Россби. Различают следующие придельные случаи:
Короткие волны ( ), длинна которых мала по сравнению с радиусом Россби. Для них следует, что
Следовательно короткие волны являться обычными бездисперсионными волнами мелкой воды. Напомним, однако, что теория мелкой воды требует, чтобы горизонтальный масштаб волн был велик по сравнению с глубиной.
Длинные волны ( ), длинна которых велика по сравнению с радиусом Россби. Для них следует, что
В этом предельном случае влияние силы тяжести отсутствует, так что частицы движутся только по инерции. По этой причине f часто называют инерционной частотой.
Для частоты меньше f получаются еще более длинные волны, на которые также не действует сила тяжести, и они являются инерционными. Значение возмущения и скоростей в области распространения значительно меньше, чем при w~f.
Все это представлено выше на графиках.
Оглавление:
Министерство образования РФ.
Российский государственный гидрометеорологический университет.
Кафедра Океанологии.
Курсовая работа.
Геострофическое приспособление волновых колебаний уровня.
Выполнил: ст. гр. О-493
Маслов П.А.
Проверил: Царев В.А.
Санкт-Петербург
2008г.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.