Математика \ Математический анализ

Ответы на контрольные задания по теме: "Дифуры", страница 3

$\displaystyle A_{1}\vec y_{1} (x_{0})+A_{2}\vec y_{2} (x_{0})= \begin{pmatrix}1... ...ec y_{1} (x_{0})+B_{2}\vec y_{2} (x_{0})= \begin{pmatrix}0\\ 1 \end{pmatrix}\,.$

Эти решения зависят от $ x_{0}$. Тогда вектор-функции

$\displaystyle \vec r_{1}=A_{1} (x_{0})\vec y_{1} (x)+A_{2} (x_{0})\vec y_{2} (x) \,,\qquad \vec r_{2}=B_{1} (x_{0})\vec y_{1} (x)+B_{2} (x_{0})\vec y_{2} (x)\,,$

являются столбцами разрешающего оператора $ R (x,x_{0})$.

Ответ: 15

Запишем однородную систему линейных дифференциальных уравнений 1-го порядка в матричном виде

$\displaystyle \vec y\,'=A (x)\vec y$


и рассмотрим матричное решение следующей задачи Коши

$\displaystyle Y'=A (x)Y\,,\qquad Y (x_{0})=I\,.$


Решение этой задачи как функция двух переменных $ (x,x_{0})$и называется разрешающим оператором для рассматриваемой системы. Обозначим его через $ R (x,x_{0})$.

Одно из важнейших свойств разрешающего оператора состоит в следующем

$\displaystyle R (x_{3},x_{2})R (x_{2},x_{1})=R (x_{3},x_{1})\,.$


При помощи разрешающего оператора можно строить как решение задачи Коши однородного уравнения

$\displaystyle \vec y\,'=A (x)\vec y\,,\qquad \vec y (x_{0})=\vec b\,,$


так и решение задачи Коши неоднородного уравнения

$\displaystyle \vec y\,'=A (x)\vec y+\vec f (x)\,,\qquad \vec y (x_{0})=\vec b\,.$

В первом случае решение дается формулой 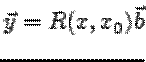$ \vec y=R (x,x_{0})\vec b$, во втором -- формулой

$\displaystyle \vec y=R (x,x_{0})\vec b+ \int\limits_{x_{0}}^{x}R (x,t)\vec f (t) \,dt\,.$

Ответ: 16

Матричная экспонента определяется как сумма ряда

$\displaystyle e^{A}=\sum_{n=0} \frac{A^{n}}{n!}\,,$

где $ A$-- квадратная матрица. Ряд сходится, поскольку каждый компонентный ряд имеет мажоранту

$\displaystyle \sum \frac{\Vert A\Vert^{n}}{n!}\,,$

где $ \Vert A\Vert$-- матричная норма.

Для вычисления матричной экспоненты можно матрицу $ A$привести к жордановой форме $ \Lambda$, при этом

$\displaystyle A=T\Lambda T^{-1}$   и$\displaystyle \qquad e^{A}=T e^{\Lambda}T^{-1}\,.$

Столбцами матрицы перехода $ T$являются собственные и присоединенные векторы матрицы $ A$, в базисе из которых она принимает жорданову форму.

Каждая жорданова клетка в матрице $ \Lambda$имеет вид $ \lambda I+N$, где $ N$-- матрица, у которой ряд выше главной диагонали занимают единички, а остальные места заполнены нулями. При этом $ N^{k}=0$, где $ k$-- порядок жордановой клетки. Тогда

$\displaystyle e^{\lambda I+N}=e^{\lambda} \Bigl(I+N+\ldots \frac{N^{k-1}}{(k-1)!} \Bigr)\,.$

Другой способ построения экспоненты состоит в следующем. Можно матричную экспоненту искать в виде многочлена степени на единицу меньше, чем порядок матрицы, при этом искомый многочлен должен совпадать с экспонентой на спектре матрицы (в случае кратных корней следует приравнивать и производные).

Ответ: 18

Рассмотрим однородную систему линейных дифференциальных уравнений с постоянными коэффициентами. Запишем ее в матричном виде

$\displaystyle \vec y\,'=A\vec y\,.$

Решение задачи Коши для этого уравнения с начальными данными 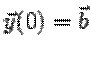$ \vec y (0)=\vec b$дается формулой

$\displaystyle \vec y= e^{Ax}\vec b\,,$

поскольку

$\displaystyle \left( e^{Ax} \right)'=A e^{Ax}$   и$\displaystyle \qquad e^{A0}=I\,.$


Разрешающий оператор для этой системы найдется как

$\displaystyle R (x,x_{0})=R (x,0)R (0,x_{0})=e^{Ax}e^{-Ax_{0}}=e^{A (x-x_{0})}\,.$

Ответ: 20

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида

$\displaystyle y'=f (x)g (y)\,.$

Функции $ f$и $ g$будем считать определенными на некоторых интервалах. Разделением переменных называется метод решения этого уравнения, при котором общее решение уравнения записывается в виде равенства

$\displaystyle \int\frac{dy}{g (y)}=\int f (x)\,dx\,.$


Однородным дифференциальным уравнением называется уравнение вида

$\displaystyle y'=f \Bigl(\frac{y}{x}\Bigr)\,.$

Аналитически оно легко сводится к уравнению с разделяющимися переменными если искать решение в виде $ y=xu (x)$. Тогда $ xu'+u=f (u)$, откуда

$\displaystyle u'=\frac{f (u)-u}{x}\,.$

Ответ: 23

Рассмотрим задачу Коши

$\displaystyle \vec y'=\vec f (x,\vec y)\,,\qquad \vec y (x_{0})=\vec b\,.$


Теорема Пикара утверждает:

Если функция $ \vec f$непрерывна и равномерно по $ x$липшицева по $ \vec y$, то в некоторой окрестности начальной точки задачи Коши последняя имеет и при том единственное решение.

При этом $ \vec f$равномерно по $ x$липшицева по $ \vec y$, если

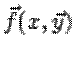$\displaystyle \vert\vec f (x,\vec y_{1})-\vec f (x,\vec y_{2})\vert\leqslant k\vert\vec y_{1}- \vec y_{2}\vert\,,$

где $ k$не зависит от $ x$. Например, для равномерной липшицевости достаточно, чтобы функция $ \vec f (x,\vec y)$была ограниченно дифференцируема по $ \vec y$.

В качестве примера рассмотрим уравнение

$\displaystyle y'=2\, \frac{y}{x}\,.$


Все его решения имеют вид 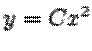$ y=Cx^{2}$. Ясно, что решения, удовлетворяющего начальному условию $ y (0)=1$, не существует. Далее, взяв начальное условие вида $ y (1)=1$мы видим, что функции, определенные равенством

$\displaystyle y= \begin{cases}Cx^{2}\,,& x<0,\\ x^{2}\,,& x\geqslant0\,, \end{cases}$

являются решением рассматриваемой задачи Коши. Таким образом, нарушается как существование, так и единственность решения задачи Коши, что связано с невыполнением условий теоремы Пикара -- функция в правой части не является непрерывной.

Второй пример, в котором нарушается липшицевость правой части имеет вид

$\displaystyle y'=3y^{2/3}\,,\qquad y (0)=0\,,$


Это уравнение кроме нулевого имеет решение 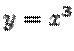$ y=x^{3}$. Нарушена единственность.

Ответ: 24

В случае уравнения

$\displaystyle F (x,y,y')=0$


можно показать, что если кривая $ x=x (t)\,, y=y (t),\, z=z (t)$лежит на поверхности $ F (x,y,z)=0$, причем в точках этой кривой выполнены соотношения

$\displaystyle \frac{\partial F}{\partial z}=0\,,\qquad \frac{\partial F}{\parti... ... \frac{\partial F}{ \partial y}=0\,,\qquad \frac{\partial F}{\partial y}\ne0\,,$


то кривая $ x=x (t)\,,\; y=y (t)$является интегральной для рассматриваемого уравнения. Это решение и называется особым. Как правило, такое решение является огибающей некоторого семейства решений уравнения. Например, в случае уравнения Клеро

$\displaystyle y=xy'-\varphi (y')$


особое решение существует и определяется системой

\begin{displaymath}\begin{cases}x=\varphi' (z)\\ y=\varphi' (z) z-\varphi (z)\,. \end{cases}\end{displaymath}


Оно является огибающей семейства решений $ y=xC-\varphi (C)$.

Скачать файл