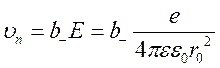Несамостоятельная проводимость воздуха. Экспериментальная установка. Решение уравнения для стационарных токов в двух предельных случаях. Развитие разряда в резко-неоднородных полях, страница 4

.

Поэтому число частиц, попавших за время Dt в слой радиуса r₀ будет:

 

.

 

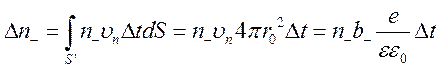Тогда число частиц, прорекомбинировавших за время Dt равно:

.

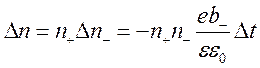Сравнивая полученное выражение с уравненимуравнением рекомбинации получим выражение для коэффициента рекомбинации (формула Ланжевена):

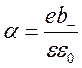
             - формула Ланжевена.

(вВ системе СГСЭ выражение для коэффициента рекомбинации будет иметь вид:

 

).

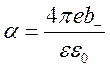
Уравнение рекомбинации при равных концентрациях положительных и отрицательных ионов (n₊ = n_{_} = n) в одномерном случае легко интегрируется:

.

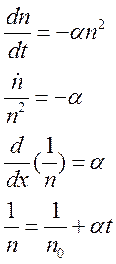Величина обратная концентрации линейно возрастает со временем.

2. Рассмотрим рРешение уравнения для стационарных токов в двух предельных случаях.

            ПедположимПредположим, что концентрация ионов n мала. Тогда можно пренебречь рекомбинацией (3.1), поскольку рекомбинационный член αn² квадратичен по пn. В этом приближении j = q∙l∙e, т. е. ток не зависит от приложенного напряжения и равен току насыщения. Этот результат справедлив в случае сильных электрических полей. Он объясняется тем, что за время, требующееся иону, чтобы пролететь в сильном электрическом поле Ε пролететь от одного электрода к другому, ионы не успевают сколько-нибудь заметно рекомбинировать. Поэтому все ионы, производимые ипони-затором, уходят на электроды. Ежесекундно на электрод поступает заряд S∙l∙q∙e. Это и есть сила тока, текущего через газ. Величина J  =  S∙l∙q∙e называется током насыщения, а величина j_s  =  q∙l∙e -— плотностью тока насыщения. Обе эти величины пропорциональны длине ионизационной камеры l, поскольку полное число ионов, производимое ионизатором, также пропорционально l.

           

Линейный участок графика зависимости тока от напряжения (рис.3.1) определяет границы применимости закона Ома: если плотность тока j настолько мала, что членом j/(el) можно пренебречь по сравнению с αn². Тогда   и формула (9)(3.1) дает закон Ома,:

 

 

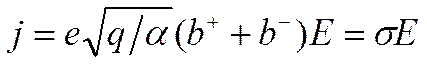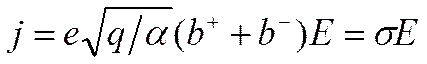
т.е. плотность тока j пропорциональна электрическому полю Е. Такой случай имеет место при малых Е. Таким образом, в слабых электрических полях выполняется закон Ома.

На рис.3.7 приведен представлен начальный, линейный участок вольтамперной характеристики разрядаВАХ в системе электродов цилиндр--цилиндр. Котангенс угла наклона линейного участка, зависимости тока от напряжения, определяет величину сопротивления воздуха: R = U/I.

R = 9*∙10¹²  Ом.

 

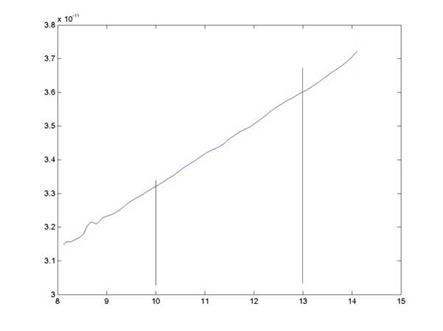
Рисунок 3.7. Начальный линейный участок вольтамперной характеристики разряда в системе электродов цилиндр-цилиндр.

Подставляя в выражение для проводимости радиусы цилиндров,

,

 

 

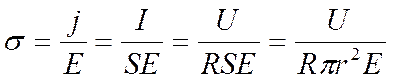
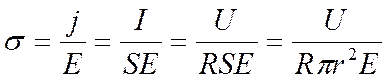получим проводимость воздуха: 0,07 пк Ссим\/м.

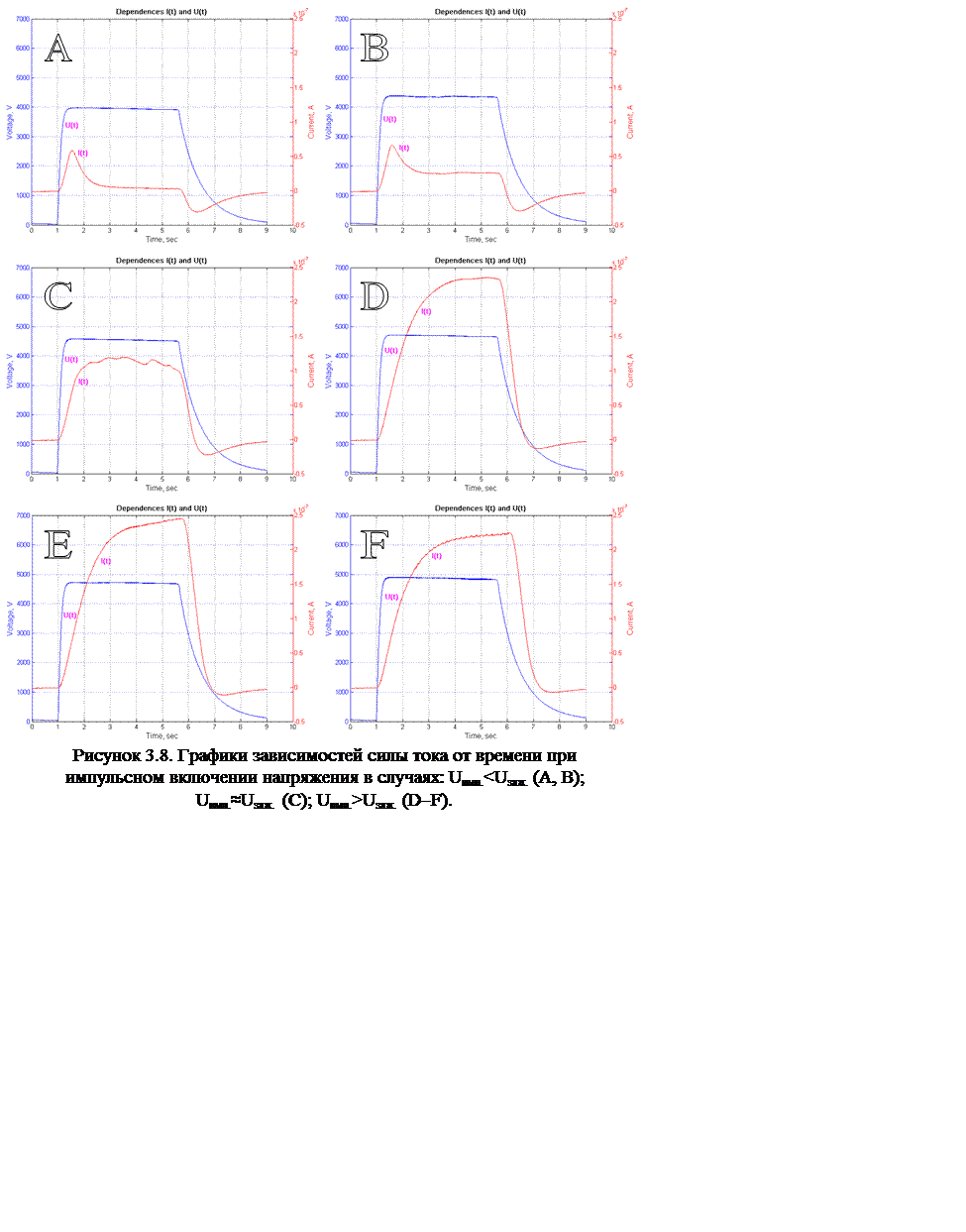
При исследовании вольтамперных характеристик разряда в системе электродов цилиндр-цилиндр ВАХ одновременно проводилась записывались зависимости тока от времени при значениях амплитудах импульсного напряжения больше и меньше напряжения зажигания короны. На рис.3.8 представлены зависимости напряжения и соответствующей силы тока от времени.

При значениях амплитуде импульсного напряжения меньше 4,5 00кВ на графике I(t) в момент включения напряжения наблюдается быстрое нарастание тока до некоторого максимума, а далее спад до каково-тонекоторого стационарного значения, (порядка сотых долей микроампера) (рис.3.8, А,B). В момент отключения напряжения происходит резкое уменьшение тока, и на некоторое время он становится отрицательным.