Материальные соотношения в электродинамике. Временная и пространственная дисперсии в линейной электродинамике. Материальные соотношения для гармонических составляющих плоских волн, страница 2

3.2. Материальные соотношения для гармонических составляющих плоских волн  и  в однородных стационарных средах. При решении уравнений в частных производных с постоянными коэффициентами удобно использовать интегральное преобразование Фурье по времени и по координатам. Это позволяет свести проблему к решению алгебраических уравнений с последующим обратным преобразованием Фурье. Если поля гармонические, то использование преобразования Фурье позволяет проводить алгебраическое исследование комплексных Фурье – образов полей. Вещественная (или мнимая) часть этих образов описывает реальные гармонические поля. Преобразование Фурье для вектора электрической индукции имеет вид

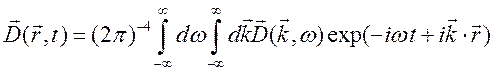                        ,             (3.3)

где  - комплексный фурье – образ вещественной функции . Отметим, что иногда в преобразовании Фурье используется другое представление экспоненты: . Переход от функции к фурье – образу делается следующим образом

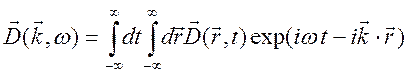                        .                           (3.4)

Будем интересоваться нестационарным процессом, возникающим при включении источника в момент времени . По принципу причинности поля отсутствуют при  и преобразование (3.4) принимает вид

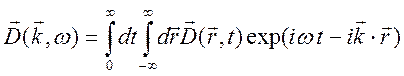.                            (3.5)

Подставляя в (3.5) представление (3.2) для функциив случае однородной стационарной среды, получим

            .

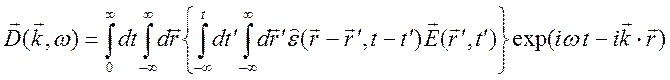Введем обозначения  и получим представление

            .

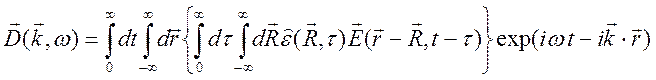Поменяем порядок интегрирования и получим выражение для фурье – образа

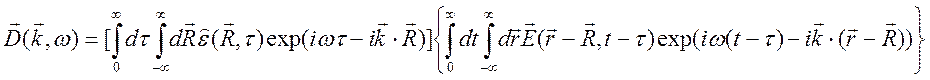Выражение в фигурных скобках представляет собой , а выражение в квадратных скобках это . Таким образом, получено материальное соотношение для фурье - образов

                                    .                                         (3.6)   

Зависимость  от частоты  отражает наличие временной (частотной) дисперсии, а зависимость от волнового вектора      это признак пространственной дисперсии.

            В линейной электродинамике можно ввести в рассмотрение материальные связи, описывающие плотности токов

                                    ,

                                    .

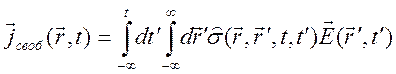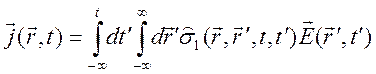В случае однородной стационарной среды получаются соотношения для фурье – образов

                                                ,

                                                 .  

3.3 Энергетические соотношения для электромагнитного поля. Уравнения Максвелла, как уже отмечалось выше, это основные постулаты электродинамики материальных сред. Важным следствием этих уравнений является закон, описывающий баланс энергии в среде при наличии электромагнитного поля. Получим его для простейшего случая неоднородной изотропной среды без временной и пространственной дисперсии, когда справедливы соотношения

                                    ,

где  - скалярная функция, описывающая диэлектрическую проницаемость неоднородной среды. Первое уравнение Максвелла

                                                 

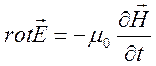
скалярно умножим на . Второе уравнение Максвелла

                                               

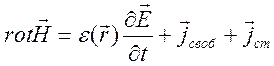
скалярно умножим на  и вычтем одно из другого

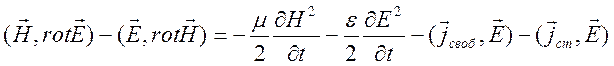            .                 (3.7)

Используя формулу

                                   

проинтегрируем соотношение (5.1) по объему , включающему сторонние источники (Рис.3.1). Если объем не зависит от времени , то получим

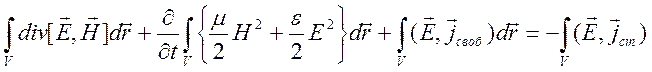            .            (3.8)

Воспользовавшись формулой Гаусса-Остроградского, преобразуем (3.9) к виду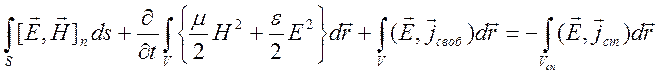,                     (3.10)

Где - поверхность, охватывающая объем , - внешняя по отношению к объему  нормаль, - объем, в котором расположены сторонние источники. Соотношение (3.9) содержит квадратичные функции, оно выражает закон сохранения энергии в изотропной среде без дисперсии. Подынтегральное выражение во втором слагаемом

                                     

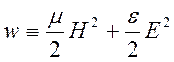
представляет собой распределенную в пространстве плотность электромагнитной энергии. Оно показывает, что всюду, где есть поля , есть и энергия.

            Плотность потока электромагнитной энергии  входит в подынтегральное выражение первого члена в (3.9). Слагаемое 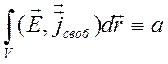- отражает потери на джоулево тепло. Интеграл 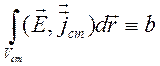 характеризует мощность стороннего источника, которую нужно затратить в объеме , чтобы электрическая и магнитная индукции изменялись со скоростям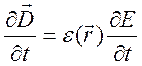и  и .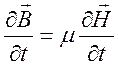

            Формула (3.9) приводится к виду

                                    .

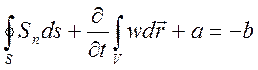            При учете дисперсии энергетическое соотношение усложняется, в него будет входить еще энергия среды (кинетическая энергия заряженных частиц). Учет анизотропии приводит к дополнительному усложнению.