Расчёт оптимального кода по методике Шеннона-Фано

Пример выполнения расчёта

Содержание:

Оглавление

1 Аннотация.............................................................................................. 5

2    Содержание задания ............................................................................ 5

3    Теоретическая часть.............................................................................. 7

3.1       Количественная оценка информации......................................... 7

3.2       Вычисление пропускной способности передачи информации и пропускной способности каналов связи ......................................................... 8

3.3       Определение избыточности сообщений. Оптимальное кодирование. .................................................................................................. 11

4    Практическая часть ............................................................................. 14

4.1       Содержание задания ................................................................. 14

4.2       Расчёт на основе исходных данных .......................................... 14

4.2.1    Определение количества информации, соответствующее одному символу сообщения, составленного из данного алфавита ........ 14

4.2.2    Вычисление теоретической скорости передачи сообщений

15

4.2.3    Вычисление избыточности сообщений, составленных из данного алфавита ....................................................................................... 15

4.2.4    Построение оптимального кода сообщения ........................ 15

5    Заключение ......................................................................................... 17

6    Библиографический список ................................................................ 18

1 Аннотация

В данной курсовой работе рассматривается алфавит из символов, появляющихся с определённой вероятностью. для которого рассчитаны различные величины: количество информации, приходящееся на символ сообщения в случае равновероятных и неравновероятных символов, недогруженность символов, скорость передачи данных и т. д.

Также для данного алфавита выполняется построение оптимального двоичного кода на основе методик Шеннона – Фано и Хаффмана.

В процессе выполнения данной курсовой работы происходит закрепление знаний, полученных при освоении дисциплины

«Информационные технологии».

2 Содержание задания

Исходные данные для выполнения курсовой работы индивидуальны и определяются на основе значения числа, для записи которого была использована младшая значащая цифра номера зачётной книжки студента.

Число, для записи которого использована данная цифра, становится исходным значением переменной m.

Для выполнения расчётов предполагается использование демонстрационной версии интегрированной среды выполнения инженерных расчётов PTC Mathcad или разработка прикладной программы средствами одного из современных языков программирования высокого уровня.

Число символов алфавита k = m + 10. Где m — номер варианта задания. Необходимо определить количество информации, соответствующее одному символу сообщения, составленного из данного алфавита:

a) если символы алфавита встречаются с равными вероятностями;

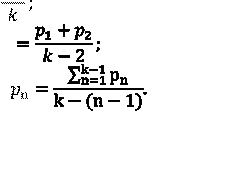b)  если символы алфавита встречаются в сообщении с

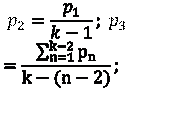
вероятностями:

Определить, насколько недогружены символы во втором случае.

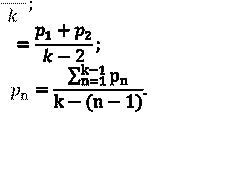
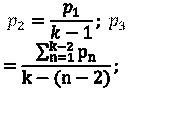
Число символов алфавита равно k. Вероятности появления символов равны соответственно:

Длительности символов:  1 = 1 с;  2 = 2 с;  k =  k-1 + 1.

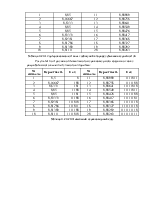
Чему равна теоретическая скорость передачи сообщений, составленных из таких символов?

Сообщения составляются из алфавита с числом символов, равным k.

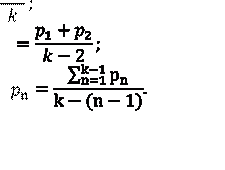
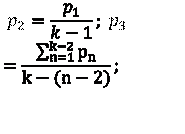
Вероятность появления символов алфавита равна соответственно:

Найти избыточность сообщений, составленных из данного алфавита. Построить оптимальный код сообщения.

3 Теоретическая часть

3.1  Количественная оценка информации

Общее количество неповторяющихся сообщений, которое может быть составлено из алфавита m, путём комбинирования по n символов в сообщении: