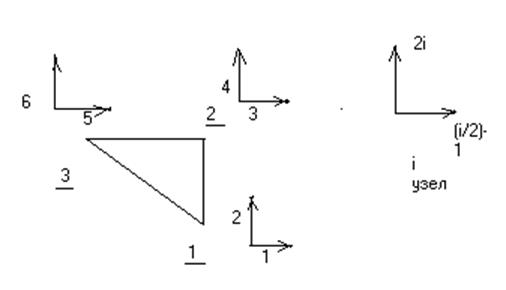
 Элемент
для составления матрицы индексов.
Элемент
для составления матрицы индексов.
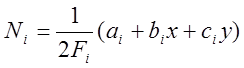 - линейные функции формы
- линейные функции формы
То есть составлена матрица жесткости элемента и вектор нагрузок ,
Тогда будет записываться в виде :
 ;
( 1)
;
( 1)
18*18 18*1 18*1
![]()
требуется исключить 17 и 18 -ое уравнения .
матрицу
жесткости [K] представляем в виде матрицы 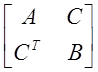 ;
;
вектор
нагрузок : 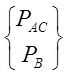 ;
;
перемещение
: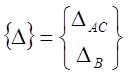 ;
;
где
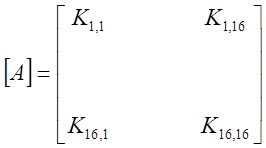 ;
; 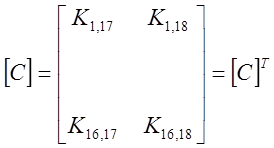 ;
;
16*16 16*2
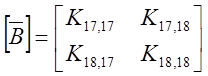
2*2
Решаем уравнение (1) :
![]()
18*1 18*18 18*1
(1а)
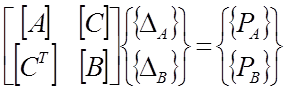 ;
;
получаем
:![]()
16*16 16*2 2*16 2*2
(а)
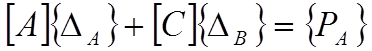
16*16 16*1 16*2
(в)
![]()
2*16 16*1 2*2 2*1 2*1
из выражения (в) получаем:
![]()
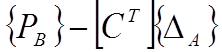
2*2 2*1 2*1 2*16 16*1
(с)
![]() ;
;
2*1 2*2 2*1 2*2 2*1 2*2 2*16 16*1
подставляем выражение (с) в выражение (а) и получаем (d) :
![]()
![]() ;
;
16*16 16*1 16*2 2*2 2*1 2*2 2*16 16*1 16*1
![]() ;
;
16*16 16*1 16*2 2*2 2*16 16*1 16*1 16*2 2*2 2*1
![]() ;
;
16*1 16*1
обозначаем ![]() ;
;
16*16
или можем записать :
![]() (2) ;
(2) ;
16*16 16*1 16*1
где 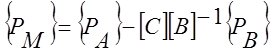 ;
;
Уравнение (2) не содержит внутренних степеней свободы .
![]()
![]() находится из уравнения (в) :
находится из уравнения (в) :
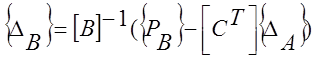 .
.
2*1 2*2 2*1 2*16 16*1
Представленное преобразование является методом конденсации (методом редукции , так как количество неизвестных уравнений понижается ) .
Недостатками этого приема является :
1) Получение системы уравнений с полнозаполненной матрицей коэффициентов ЛАУ .
Решать такую систему необходимо методами или подпрограммами
GELB , то есть подходящими для общего вида ;
2)
Необходимо выполнить обращение
выделенного фрагмента матрицы жесткости ![]() и
выполнять много умножений и транспонирований , то есть требуются
специальная программа мат . обеспечений .
и
выполнять много умножений и транспонирований , то есть требуются
специальная программа мат . обеспечений .
Вывод. Очевидно , что решение больших систем уравнений оправдано при использовании данного подхода к стационарным процессам , тем не менее этот подход используется с 80-ых годов в методах расчета динамики конструкции.
3.2. РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Подпрограмма GELB с обычной (DGELB с удвоенной) точностью. Подпрограмма предназначена для решения системы уравнений вида
АХ= R,
где
А — ленточная матрица коэффициентов порядка M; R — матрица правых частей
системы уравнений размером М ![]() N. Система уравнений
решается методом исключения Гаусса с выбором главного элемента в столбце, что
сохраняет ленточную структуру матрицы в процессе преобразований. Если в
качестве R задается единичная матрица, то решение Х будет обратной к А
матрицей.
N. Система уравнений
решается методом исключения Гаусса с выбором главного элемента в столбце, что
сохраняет ленточную структуру матрицы в процессе преобразований. Если в
качестве R задается единичная матрица, то решение Х будет обратной к А
матрицей.
Обращение к подпрограммам имеет соответственно вид:
САLL GELВ (R, А, М, N, MUD, MLD, EPS, IER)
CALL DGELB (R, А, М, N, MUD, MLD, EPS, IER)
А — массив длиной МА, первые МЕ элементов которого содержат исходную матрицу коэффициентов, расположенную по строкам. Предполагается, что в памяти хранятся только элементы главной диагонали, а также элементы MUD верхних и MLD нижних кодиагоналей (точность обычная или удвоенная):
МА = М* МС — (МС — MLD — 1) (МС — MLD)/2
МЕ = МА — (МС — MUD — 1) (МС — MUD) /2
МС = min (М, MUD + М1 0+ 1);
MUD — число верхних кодиагоналей, т. е. кодиагоналей выше главной диагонали;
MLD — число нижних кодиагоналей, т. е. кодиагоналей ниже главной диагонали;
IER — индикатор ошибки, принимающий следующие значения:
IER =0 свидетельствует, что в процессе работы подпрограммы ошибок не было;
IER = — 1 означает, что либо
нарушены ограничения MUD ![]() 0, MLD
0, MLD ![]() О, МUD + MLD
О, МUD + MLD![]() 2M — 2,
либо главный элемент на каком-то шаге исключения равен нулю;
2M — 2,
либо главный элемент на каком-то шаге исключения равен нулю;
IER = К указывает на потерю точности.
В, М, N, EPS — параметры, имеющие тот же смысл, что и одноименные параметры подпрограмм GELG (DGELG) .
C
C ..................................................................
C
C SUBROUTINE GELB
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.