Особенности формирования матриц физико-механических, теплофизических и других свойств, в условиях возможного изменения параметров, страница 2

Где  h- коэффициент  теплообмена; T – температура  на  границе (неизвестная), К; Т (бесконечность)- температура  окружающей  среды (известная), K; l- направляющие  косинусы; q- поток  тепла, который  считается  положительным, если  тепло  теряется  телом. Поток  тепла q- и  конвективная  потеря  тепла  h(T-Tбескон.)  не  имеют  места  на  одном  и  том  же  участке  поверхности  границы. Если  существуют  потери  тепла  за  счет  конвекции, то  отсутствует  отвод  или  приток  тепла  за  счет  теплового  тепла  и  обратно.

Уравнения  (13) и (13.2)  могут  быть  применены  к  одномерным  и  двумерным  задачам  после  простого  вычеркивания  членов, связанных  с  ненужными  координатами. Уравнение  для  одномерной  задачи  записывается  в  виде

с  граничным  условием

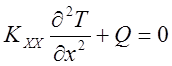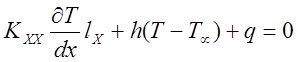Если  конвективный  теплообмен  отсутствует  и, кроме  того, поток  тепла  равен  нулю, то  уравнение  (13.2)  сводится  к  соотношению:

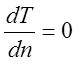которое  выражает  условие  существования  теплоизолированной  границы  (n- внешняя  нормаль).

Запишем  матрицу  теплопроводности  элемента:

Матрица                   
           содержит  функции  формы, причем

Матрица                    содержит  значение  коэффициентов  теплопроводности.

А  матрица                   получается  дифференцированием  N  по  X  и  Y и  Z. Соотношение  

для  определения  B  имеет  вид

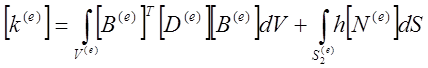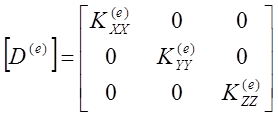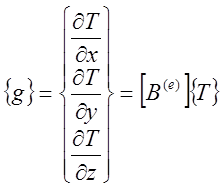Вектор-столбец  правых  частей  уравнения  для  элемента  определяется  формулой,

где  величины  Q, q, T, h  имеют  заданные  числовые  значения.

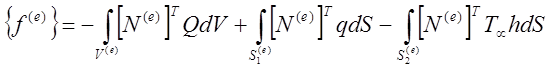                          Вышеприведенные  формулы  содержат  все  данные, необходимые  для  составления  матриц  элементов  в  задаче  о  переносе  тепла  за  счет  теплопроводности. Далее  рассмотрим  уравнения  для  отдельного  элемента,  поэтому  верхний  индекс  (е)  будет  опущен  во  всех  обозначениях  матриц  элементов, исключая  случай, когда  необходимо  различать  два  различных  элемента.

                          Интерполяционный  полином  для  одномерного  линейного  элемента  имеет  вид,

где

Эти  функции  формы  определены  относительно  системы  координат, показанной  на  рис. 2. Элемент  имеет  длину  L. Матрицы  в  (15.1)  и  (17)  принимают  вид:

Поэтому

Матрица  свойств  материалов  сводится  к  одному  коэффициенту:

Вычислим  интегралы  в  (15):

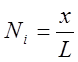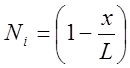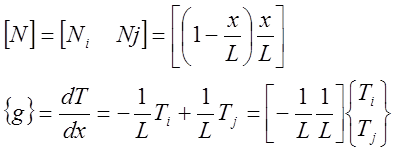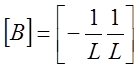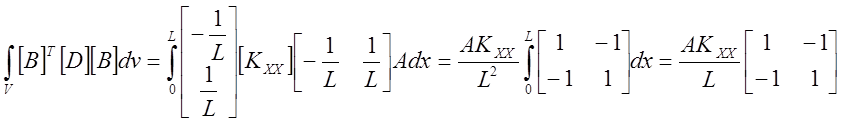Площадь  поперечного  сечения  при  этом  предполагается  постоянной.

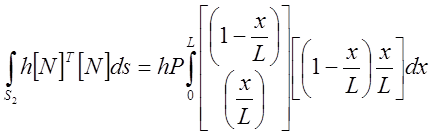Так  как   dS=Pdx, где  Р- периметр. Периметр  тоже  предполагается  неизменным  вдоль  оси  X. Производя  перемножение  в  (21.2)  и  вычисляя  интеграл, имеем

Матрица  теплопроводности  получается  сложением  матриц  (21.1)  и  (21.3):

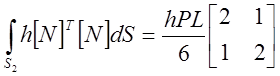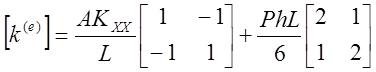Член  в  (21.4), описывающий  конвекцию, исчезает, если  h  равно  нулю  на  границе  элемента.

Вычисление  интегралов  в  векторе  сил  элемента   (18)  дает

Так  как  третий  интеграл  идентичен  по  форме  второму, можно  сразу  же  записать

 

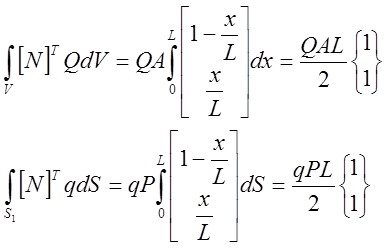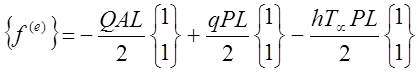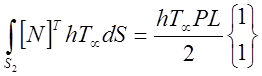Полное  выражение  теперь  имеет  вид

Это  выражение  можно  переписать  как

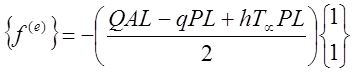Примером  одномерной  задачи  переноса  тепла  является  задача  об  охлаждении  стержня. Рассмотрим  стержень, один  конец  которого  соединен  с  источником  тепла; через  боковую  поверхность   стержня  и  другой  его  конец  тепло  отводится  в  окружающую  среду. Формулы  (21.6) и (22)  предпологают, что  потери  тепла  за  счет  конвекции  происходят  только  то  боковой  поверхности. Теперь  рассмотрим  соотношения, которые  связаны  с  отводом  тепла  от  конца  одномерного  элемента.

Предположим, что  тепло  отводится  через  поверхность  правого  конца  стержня  (узел j). Потеря  (приток)  тепла  происходит  либо  в  результате  конвективного  теплообмена, либо  из-за  наличия  заданного  теплового  потока  q. Поэтому  должны  быть  рассмотрены  только  поверхностные  интегралы. Рассмотрим  поверхностный  интеграл  в  матрице  теплопроводности:

Так  как  нас  интересует  поверхность  в  j-м  узле, то

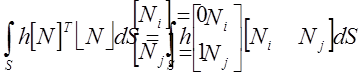И  в  результате  подстановки  этих  величин  имеем 

Эта  матрица  должна  добавляться  к  сумме  матриц  (21.4), если  на  свободном  конце  происходит  потеря  тепла. Ясно, что  коэффициент  теплообмена  в  (23)  может  отличаться  от  коэффициента, который  задан  на  боковой  поверхности. Поверхностные  интегралы  в  матрице  f  принимают  вид

Матрица  теплопроводности  при  двумерном  переносе  тепла.

                          Треугольный  элемент  с  тремя  узлами  широко  используется  для  решения  двумерных  задач  теплопроводности. Вспомним  функции  формы  для  линейного  треугольного  элемента:

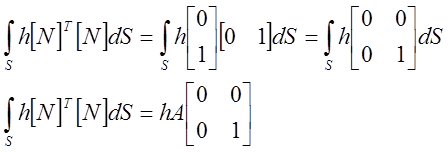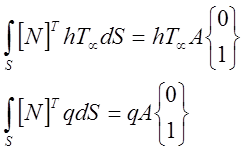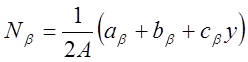Температура  дается  формулой,

где  Т- значение  температуры  в  узлах, последовательно  проходимых  от  узла  i  в  направлении, противоположном  направлению  часовой  стрелки.

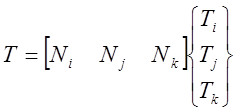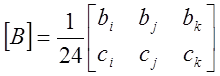Запишем  матрицу  градиентов  [B]

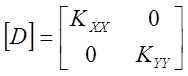И  матрицу  свойств  материалов  [D]