Продолжение таблицы 1.2.
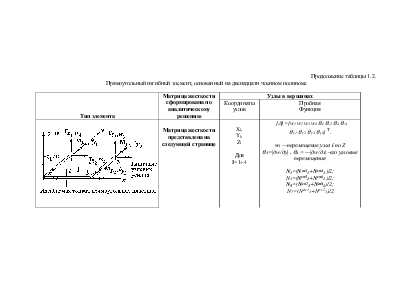
Прямоугольный изгибный элемент, основанный на двенадцати членном полиноме
|
Тип элемента |
Матрица жесткости сформирована по аналитическому решению |
Узлы в вершинах |
|
|
Координаты узлов |
Пробная Функция |
||
|
|
Матрица жесткости представлена на следующей странице
|
XI, YI, ZI Для I=1¸4 |
{D}=[w1 w2 w3 w4 qx1 qx2 qx3 qx4 q y1 q y2 q y3 q y4] т.
wi —перемещение узла i по Z qxi=|дw/ду| , qyi = —|дw/дx|-его угловые перемещения
N1=(Ne=31+Ne=41 )/2; N3=(Ne=52+Ne=61 )/2; N5=(Ne=73+Ne=82)/2; N7=(Ne=13+Ne=23 )/2
|
Продолжение таблицы 1.2.
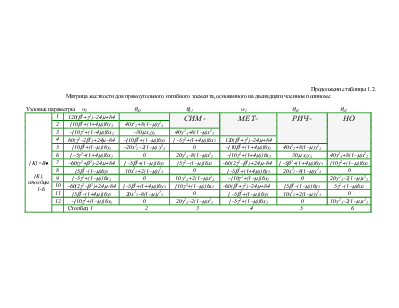
Матрица жесткости для прямоугольного изгибного элемента, основанного на двенадцати членном полиноме
Узловые параметры w1 qX1 qY1 w2 qX2 qY2
|
[K]=B· [K], столбцы 1-6 |
1 |
120(b2+g2)-24m+84 |
СИМ- |
МЕТ- |
РИЧ- |
НО |
|
|
2 |
[10b2+(1+4m)]6y3 |
40x22+8(1-m)y23 |
|||||
|
3 |
-[10g2+(1-4m)]6x2 |
-30m x2y3 |
40y23+8(1-m)x22 |
||||
|
4 |
60(g2-2b2)+24m-84 |
-[10b2+(1-m)]6y3 |
[-5g2+(1+4m)]6x2 |
120(b2+g2)-24m+84 |
|||
|
5 |
[10b2+(1-m)]6y3 |
-20x22-2(1-m) y23 |
0 |
-[10b2+(1+4m)]6y3 |
40x22+8(1-m)y23 |
||
|
6 |
[-5g2+(1+4m)]6x2 |
0 |
20y23-8(1-m)x22 |
-[10g2+(1+4m)]6x2 |
30m x2y3 |
40y23+8(1-m)x22 |
|
|
7 |
-60(g2+b2)-24m+84 |
[-5b2+(1-m)]6y3 |
[5g2-(1-m)]6x2 |
-60(2g2-b2)+24m-84 |
[-5b2+(1+4m)]6y3 |
[10g2+(1-m)]6x2 |
|
|
8 |
[5b2-(1-m)6y3 |
10x22+2(1-m)y23 |
0 |
[-5b2+(1+4m)]6y3 |
20x22-8(1-m)y23 |
0 |
|
|
9 |
[-5g2+(1-m)]6x2 |
0 |
10 y23+2(1-m)x22 |
-[10g2+(1-m)]6x2 |
0 |
20y23-2(1-m)x22 |
|
|
10 |
-60(2g2-b2)+24m-84 |
[-5b2+(1+4m)]6y3 |
[10g2+(1-m)]6x2 |
-60(b2+g2)-24m+84 |
[5b2-(1-m)]6y3 |
5g2-(1-m)6x2 |
|
|
11 |
[5b2-(1+4m)]6y3 |
20x22-8(1-m)y23 |
0 |
[-5b2+(1-m)]6y3 |
10x22+2(1-m)y23 |
0 |
|
|
12 |
-[10g2+(1-m)]6x2 |
0 |
20y23-2(1-m)x22 |
[-5g2+(1-m)]6x2 |
0 |
10y23-2(1-m)x22 |
|
|
Столбец 1 2 3 4 5 6 |
|||||||
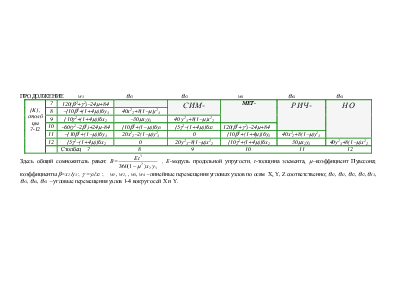
ПРОДОЛЖЕНИЕ w3 qX3 qY3 w4 qX4 qY4
|
[K], столбцы 7-12 |
7 |
120(b2+g2)-24m+84 |
СИМ- |
МЕТ- |
РИЧ- |
НО |
|
|
8 |
-[10b2+(1+4m)]6y3 |
40x22+8(1-m)y23 |
|||||
|
9 |
[10g2+(1+4m)]6x2 |
-30mx2y3 |
40 y23+8(1-m)x22 |
||||
|
10 |
-60(g2-2b2)+24m-84 |
[10b2+(1-m)]6y3 |
[5g2-(1+4m)]6x2 |
120(b2+g2)-24m+84 |
|||
|
11 |
-[10b2+(1-m)]6y3 |
20x22-2(1-m)y23 |
0 |
[10b2+(1+4m)]6y3 |
40x22+8(1-m)y23 |
||
|
12 |
[5g2-(1+4m)]6x2 |
0 |
20y23-8(1-m)x22 |
[10g2+(1+4m)]6x2 |
30mx2y3 |
40y23+8(1-m)x22 |
|
|
Столбец 7 8 9 10 11 12 |
|||||||
Здесь
общий сомножитель равен: B=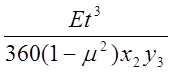 , E-модуль
продольной упругости, t-толщина элемента, m-коэффициент
Пуассона; коэффициенты b=x2 /y3 ; g =y1/x2 ;
w1 , w2, , w3, w4 - линейные перемещения угловых узлов по осям Х, Y, Z
соответственно; qX1, qX1, qX2, qY2, qX3, qY3, qX4, qY4 -угловые перемещения узлов 1-4 вокруг осей Х и Y.
, E-модуль
продольной упругости, t-толщина элемента, m-коэффициент
Пуассона; коэффициенты b=x2 /y3 ; g =y1/x2 ;
w1 , w2, , w3, w4 - линейные перемещения угловых узлов по осям Х, Y, Z
соответственно; qX1, qX1, qX2, qY2, qX3, qY3, qX4, qY4 -угловые перемещения узлов 1-4 вокруг осей Х и Y.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.