Конструкция и условия эксплуатации резиновых амортизаторов

1.  ПОСТАНОВКА ЗАДАЧИ

1.1. Конструкция и условия ее эксплуатации

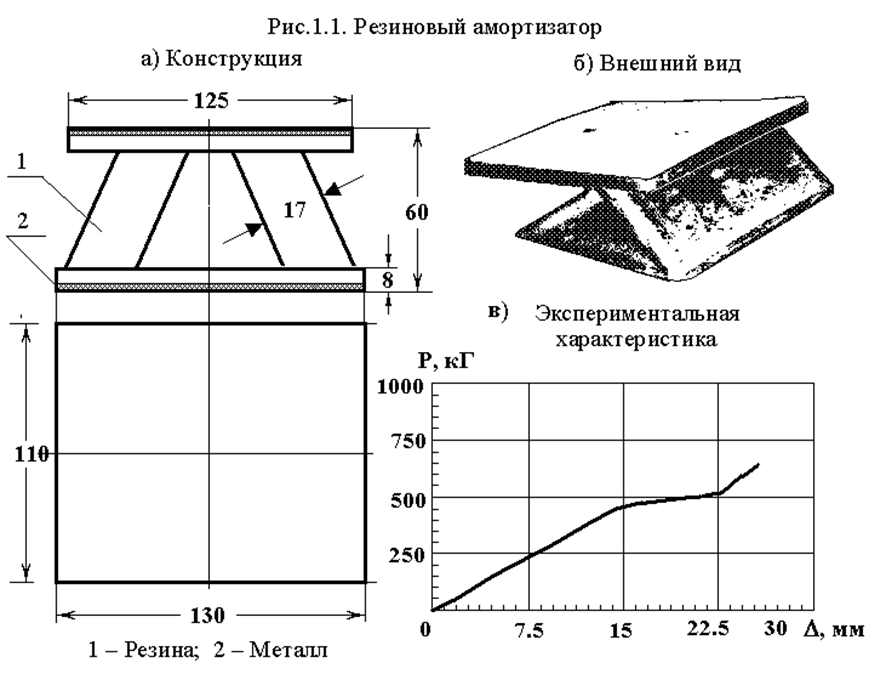Эффективность эксплуатации механических систем связанных с обеспечением задач транспортировки, подъема и рабочих нагрузок при запуске ряда изделий военной техники основана на применении резиновых амортизаторов, состоящих из совокупности единичных элементов (рис.1.1.).

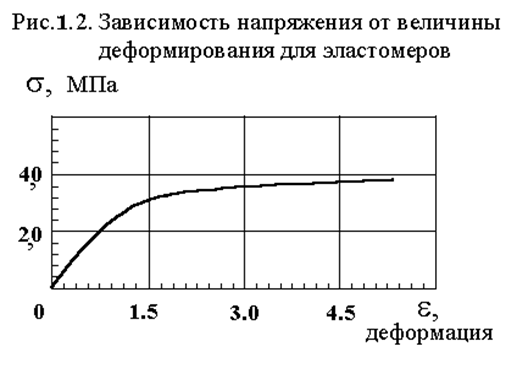
При нагружении подобных амортизаторов возможна потеря их устойчивости, что требует проработки ряда вариантов конструкций для более точного знания зависимости «продольное усилие – перемещение». Потеря устойчивости таких конструкций в большей степени связана с физической нелинейностью, а данном случае даже в пределах упругих деформаций. Так, надо отметить, что резина имеет значительный запас деформирования (до 500% и более) до начала разрушения. Конструкция не имеет элементов протяженных размеров в направлении сжатия, которые смогли бы потерять устойчивость по Эйлеру и, в большей степени, по Ясинскому, то есть является в основном физической природы. Физико–механические свойства материалов конструкции приведены в таблице 1.1. Типовая диаграмма испытаний на разрушение высокоэластичных материалов приведена на рис. 1.2. Предполагается, что характер распределения нагрузки на верхнюю и нижнюю плоскости равномерный, без перекосов при различном уровне нагружения и потере устойчивости. Кроме того, рассматриваемое нагружение с потерей устойчивости не является типовым или стандартным нагружением, иначе бы конструкция скорее всего приобрела бы более ”обтекаемый” вид. Очевидно, и то обстоятельство, что проводить испытания в натурных условиях является чрезмерно дорогостоящей операцией, как по уровню экономики, так и по уровням безопасности.

Таблица 1.1

        Физико-механические свойства материалов конструкции

Марка Материала	E, МПа	sв, Мпа	sт, 0,2 Мпа	n, Коэф. Пуссона	tср , Мпа	d,  %	Y,  %	Ан, КГм/см2	r×10-3 кг/см3
АМг3М Резина	7.1×105  400	190   38	140 –	0.30 0.48 – 0.5	175   –	23 650	50   –	2.79  –	0.00267 0.00092

В связи с этим актуален вопрос разработки програм-мных средств на основе численных методов расчета учитывающих:

·  физико – механические характеристики материалов полученных эксперименталь-но, либо взятых из литературных источников;

·  смещение элементарных объемов материала конструкции в пространстве при потере физической устойчивости;

·  возможность изменения материалов конструкции (их свойств) и зависимости «продольное усилие – перемещение».

1.2. Обсуждение требований к алгоритму моделирования

Во многих случаях на выбор алгоритма решения влияет экономический фактор. При вложении незначительных средств программисту, как правило, необходимо в большей мере ориентироваться на уже имеющиеся программы, чтобы с минимальными для себя затратами своего личного времени и сил создать некоторый, приемлемый для эффективного использования, алгоритм.

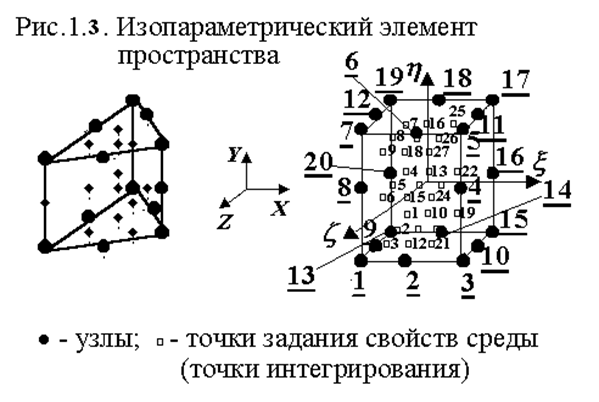
Анализ типовой экспериментальной характеристики (рис.1.1.в) показывает, что необходимо использовать пространственные высокоточные элементы вида (рис.1.3), в которых возможно задание физико–механических свойств по точкам интегрирования. При этом желательно учитывать и большие деформации. Это требует введения дополнительных производных в тензоре деформации. Однако такой алгоритм естественно станет значительно дороже и более трудоемким. Кроме того, учет самой связи (закона Гука) между тензорами напряжений и деформаций, которая, в даже в наиболее простой форме является функцией, является для описания и программирования достаточно трудоемкой. В данном же случае требуется уметь выполнять задание функций произвольного вида, так как предполагается применение алгоритма для решения других подобных задач. Использование сочетания вращательных и линейных степеней свободы в элементах таких задач, чаще всего приводит к сбросу решения получаемой системы уравнений из–за плохой обусловленности матрицы упругих коэффициентов, изменяющихся в процессе решения как по физико–механическим свойствам, так и по геометрическим размерам.

ВЫВОДЫ

1.  Исходя из изложенного необходимо избрать в качестве базового конечный элемент пространства с наиболее простой геометрической формой, линейными степенями свободы и большим количеством точек интегрирования для обеспечения возможности более точного учета изменения свойств материалов в элементе.

2.  Необходимо создать алгоритм учета свойств материалов на всем протяжении нагружения.

3.  Алгоритм решения системы уравнений, по-видимому, должен быть пошаговый, выполняющий условия сходимости по схеме Ньюмарка (по текущему модулю) или по схеме Ньютона – Рафсона (по секущему модулю), а лучше всего смешанным.

4.  Направление линии действия нагрузки в процессе решения полагается неизменным, если не будет существенного искажения геометрической формы опорных плоскостей.