Решение системы линейных уравнений с симметричной положительной полуопределенной матрицей

        1.3 Тестовый пример. Сравнение численных результатов

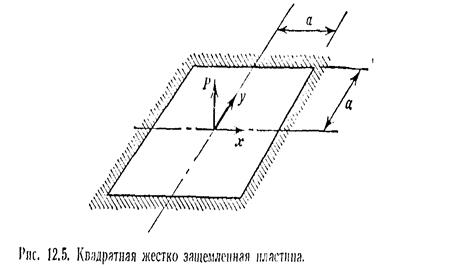
Рассмотрим в начале жестко закрепленную квадратную пластину 2а2a, на которую в центре действует сосредоточенная сила P_i (рис.2) Учитывая симметрию относительно двух осей, можно

исследовать эту задачу ,используя лини, одни элемент для четверти пластины, введя при этом лишь одну степень свободы: перемещение  под сосредоточенной силой. В этом случае P₁=к₁₁,P=P₁ / 4, x₂=y₂=a.Согласно табл.12.1(см. стр. 389),для формулировки с использованием 12 членов имеем

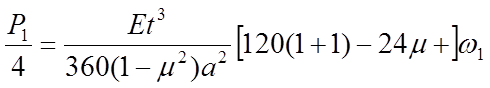
или, полагая D=Et^з\12(1-), =0.3, имеем =0.0237 (a²P₁/D). Используя коэффициенты жесткости из (8) для шестнадцатичленной формулировки, получим ,=0.0212(a²P₁/D).

         Точное решение (2) равно =0.0224(a²P₁/D), поэтому каж­дое из решений приблизительно на 8% отличается от точного , на­ходясь по разные стороны от него. Как и предполагалось, «согласованное» (шестнадцатичленное) решение ограничивает снизу точ­ное решение.

        На рис. 3 представлена задача, рассматриваемая при сравне­нии различных формулировок пластинчатых элементов при изги­бе. В задаче определяются перемещения, вызванные действием со­средоточенной силы, приложенной в центре свободно опертой пла­стины. Приводимые графики

вычислений отражают зависимость возникающей при численном определении перемещений ошибки от размеров сетки, разбиения квадранта пластины.                                                                                                                                                                    Следует отметить, что представленные результаты не обязатель­но определяют нужные параметры для сравнения точности и эффективности, так же как н размеры ячейки не обязательно являются наиболее точной мерой затраченных усилии. Такие величины, как напряжение или энергия деформации, являются более существенными параметрами, характеризующими поведение конструкции. Наиболее предпочтительной мерой затраченных усилий могли бы служить такие факторы, как затрачиваемые усилия при программи­ровании алгоритма, затраты на решение системы 

уравнений и интерпретацию полученных результатов. В данной главе графики главным образом приводятся для того, чтобы выяснить верхнюю и нижнюю границы решений, продемонстрировать               

сходимость и оценить альтернативы внутри ограниченного числа форм элементов и процедур их построения.

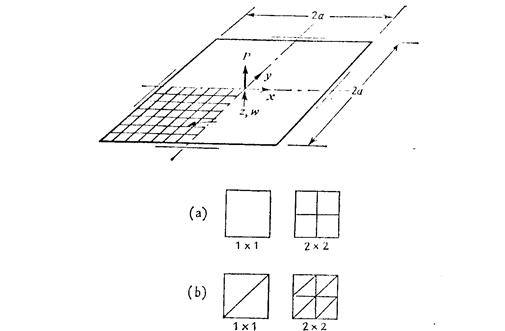
Рис. 3 Задачи для сравнения вычислительных аспектов, (a) Сетки для прямоугольных элементов; (Ь) сетки для треугольных элементов. Показаны лишь, представительные образцы сеток. Здесь также используются сетки, повернутые на 90^о.

На рис. (4 ) приведены результаты для различных формулировок прямоугольных элементов. Заметим, что двенадцатичленный полином стремится к точному решению сверху, так как условия межэлементной непрерывности перемещений нарушаются, характеристика, соответствующая «нижней границе», которая получается с использованием принципа минимума потенциальной энергии , не достигается. Наоборот, формулировка с использованием шестнадцатичленного полинома и разбиения элемента на подобласти ,обусловливает сходимость и обеспечивает достижение нижней границы для получающихся решений. На этом же рисунке приведены результаты для двух формулировок на базе модифицированного функционала Рейсснера. В одной из них вводится линейное поле изгибающих моментов и поле граничных поперечных смещений. В другой используются квадра­тичные функции. Очевидно, что существенное увеличение точности вытекает из увеличения порядка этих функций.

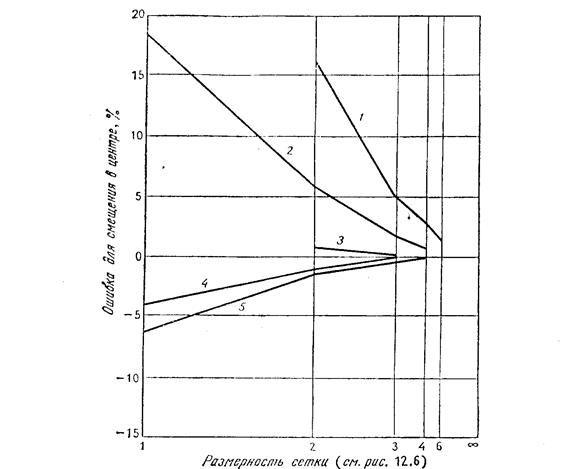
рис. 4. Сравнение численных результатов: четырехугольные конечно-элемент­ные формулировки; 1— смешанная формулировка с линейными М и ; 2 — двенадцатичлсннын полином ; 3 — смешанная формулировка с квад­ратичными М и ; 4 — шстнадцатичленный полином ; 5 — согла­сованные четырехугольные подоблсати.