


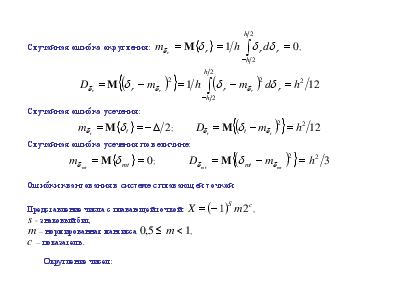










Лекция 5. Цифровая фильтрация радиосигналов
Синтез цифровых фильтров
Синтез цифрового фильтра = выбор структуры фильтра + расчет весовых коэффициентов
Структуры цифровых фильтров:
- каноническая,
- транспонированная,
- последовательная форма,
- параллельная форма
Классификация методов синтеза цифровых фильтров:
- по типу получаемого фильтра - методы синтеза рекурсивных фильтров, методы синтеза нерекурсивных фильтров, и.т.д.,
- по наличию аналогового прототипа - с использованием аналогового прототипа, прямые методы синтеза без использования прототипа.
Виды аналоговых прототипов:
Критерии синтеза цифровых фильтров:
- равномерность АЧХ в полосе пропускания,
- линейность фазочастотной характеристики (ФЧХ) – КИХ-фильтры,
- подавление в полосе подавления
Источники ошибок при реализации цифровых фильтров:
- конечное число разрядов входных и выходных дискретных последовательностей,
- квантованием значений коэффициентов алгоритмов фильтрации,
- конечной разрядностью регистров сдвига последовательностей.
Шумы в цифровых фильтрах
Ошибка квантования коэффициентов
Ошибка округления
- округление данных
- усечение данных
Квантование результатов – для сигнала большого уровня отражается шумом квантования
Для сигналов малого уровня – могут возникать предельные циклы
Арифметические операции с фиксированной точкой
- переполнение разрядной сетки
- предельный цикл переполнения сумматора
Ошибки квантования в цифровых фильтрах с фиксированной точкой
{0.0011}×{0.1001}={0.00011011} – результат перемножения двоичных чисел
Длина буфера = двойной длине слова
Длина буфера = одной длине слова
Размер слова = ![]() бит
справа от децимальной точки
бит
справа от децимальной точки
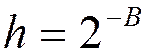 - шаг квантования
- шаг квантования
![]() - точное
значение числа
- точное
значение числа
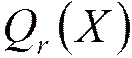 - округленное
значение = ближайшее значение к неквантованному,
- округленное
значение = ближайшее значение к неквантованному,
- ошибка округления 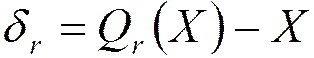 ,
, 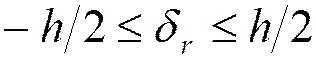
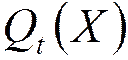 - усеченное
значение = отбрасывание младших разрядов,
- усеченное
значение = отбрасывание младших разрядов,
- ошибка усечения 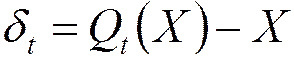 ,
, 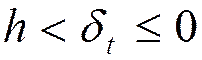
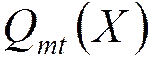 - усеченное
по величине значение = изменяет ближайшее квантованное значение, имеющее
величину, меньшую или равную точному значению
- усеченное
по величине значение = изменяет ближайшее квантованное значение, имеющее
величину, меньшую или равную точному значению
- ошибка
усечения 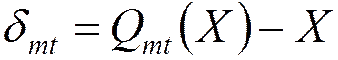 ,
, 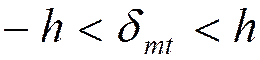
Ошибка квантования = случайная величина с равномерным распределением
Случайная ошибка округления: 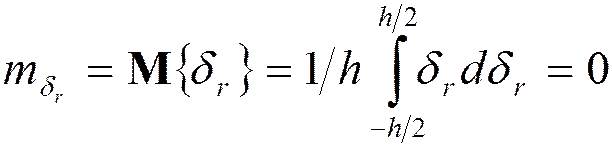 ,
,
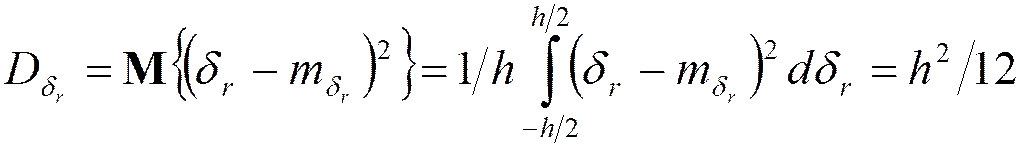
Случайная ошибка усечения:
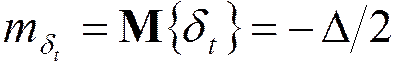 ;
; 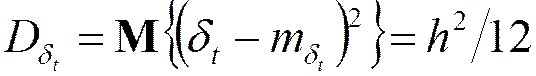
Случайная ошибка усечения по величине:
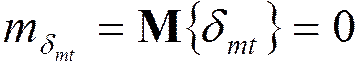 ;
; 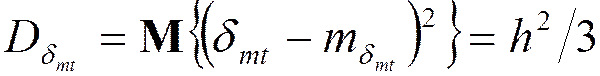
Ошибки квантования в системе с плавающей точкой
Представление числа с плавающей точкой: 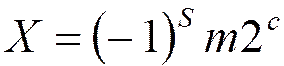 ,
,
![]() -
знаковый бит,
-
знаковый бит,
![]() – нормированная
мантисса
– нормированная
мантисса 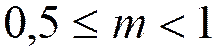 ,
,
![]() – показатель.
– показатель.
Округление чисел:
- относительная ошибка : 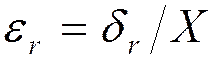 .
.
- результат квантования
чисел с плавающей точкой 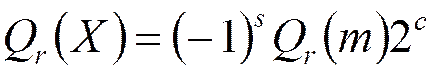
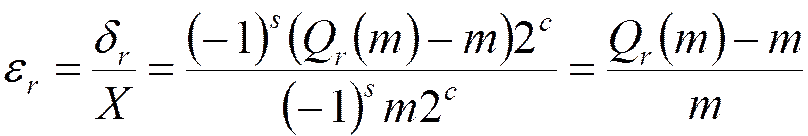
1) квантованная ![]() бит
мантисса:
бит
мантисса: 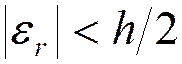 .
.
2) мантисса нормализована 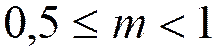 :
: 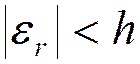 .
.
Если:
![]() равномерно
распределена на интервале
равномерно
распределена на интервале 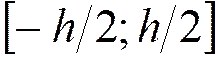
![]() равномерно
распределена на
равномерно
распределена на 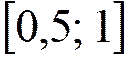
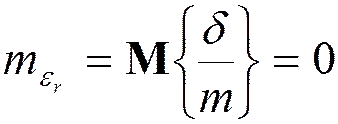 ;
; 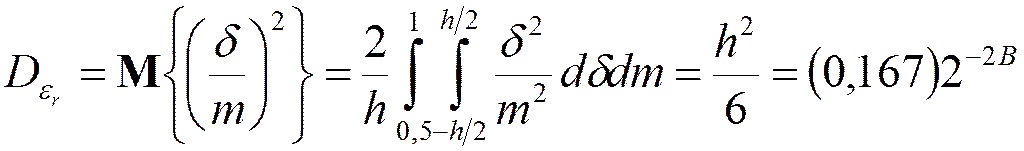 .
.
На практике распределение мантиссы ![]() может отличаться от равномерного:
может отличаться от равномерного:
- измерения
шума округления дают результат 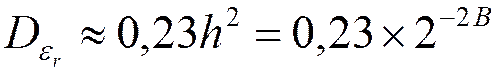
- результат теоретического и экспериментального анализа
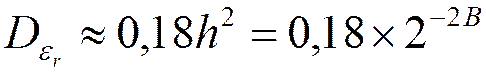 .
.
Шум округления в цифровых фильтрах
Допущения при анализе:
- ошибки округления являются некоррелированными, стационарными случайными процессами,
- произведение 2-х ошибок квантования пренебрежимо мало, например 2-15=2-15=2-30≈0
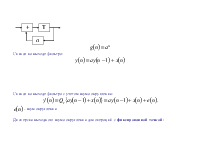
На вход цифрового фильтра
подается некоррелированная последовательность 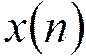 ,
, 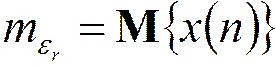 ,
, 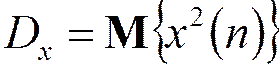
Отклик цифрового фильтра: 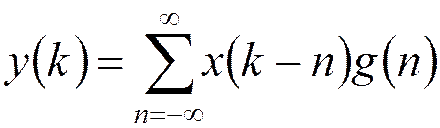 ,
,
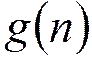 -
импульсная характеристика цифрового фильтра
-
импульсная характеристика цифрового фильтра
Вероятностные характеристики выходного сигнала:
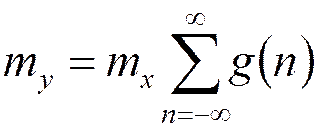
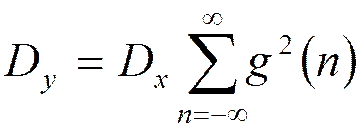
Шум округления в КИХ-фильтрах с фиксированной и плавающей точкой
Отклик цифрового КИХ-фильтра: 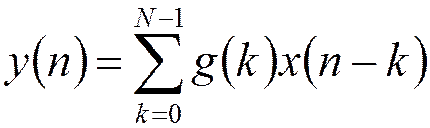 ,
,
![]() -
порядок фильтра.
-
порядок фильтра.
Операции с фиксированной точкой: округление только результатов умножения приводит к появлению выходного шума с дисперсией:
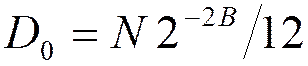
Операции с фиксированной точкой: использование для результатов умножения регистра двойной разрядности приводит к появлению выходного шума с дисперсией:
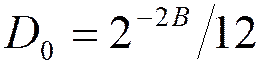
Расчет шума округления с плавающей точкой.
Пусть порядок фильтра ![]() =4.
=4.
Процесс на выходе фильтра: 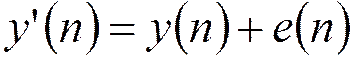 ,
,
- 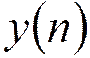 неискаженная
составляющая сигнала
неискаженная
составляющая сигнала
- 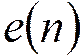 погрешность
округления
погрешность
округления
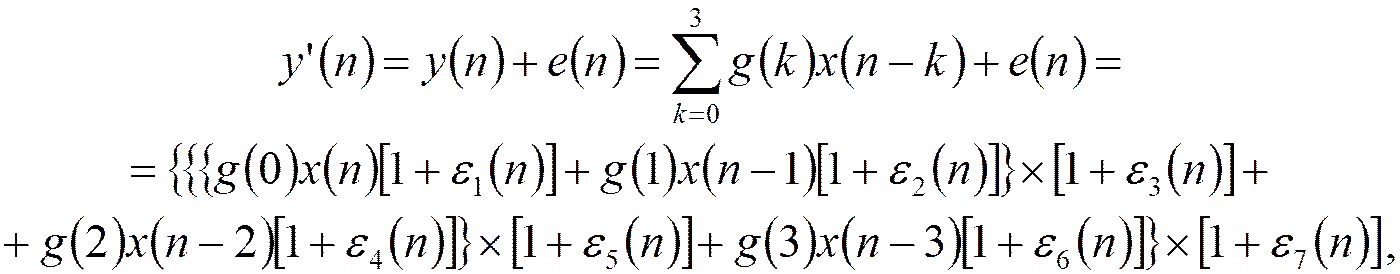
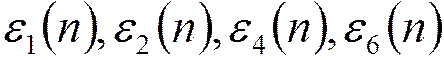 - нормированные
ошибки при умножении
- нормированные
ошибки при умножении
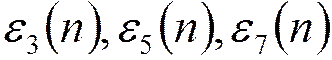 - нормированные
ошибки при суммировании
- нормированные
ошибки при суммировании
Выделим значение шума округления в плавающей точкой:
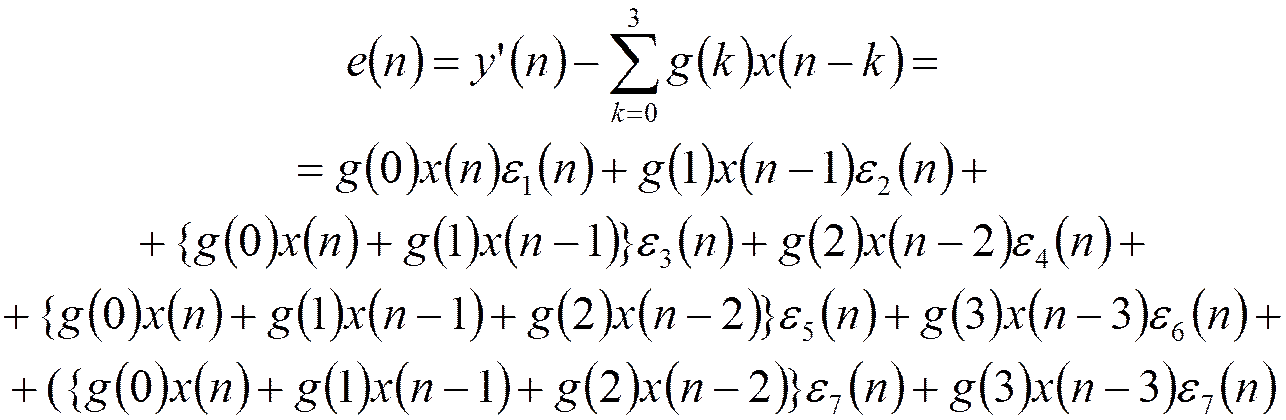
Дисперсия шума округления с плавающей точкой:
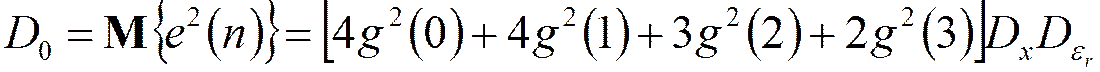 .
.
Для произвольного порядка фильтра:
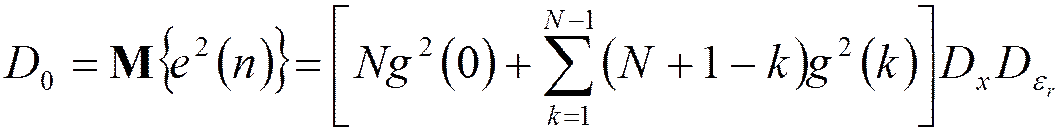 .
.
Шум округления в БИХ-фильтрах с фиксированной точкой
Импульсная характеристика БИХ фильтра 1-го порядка:
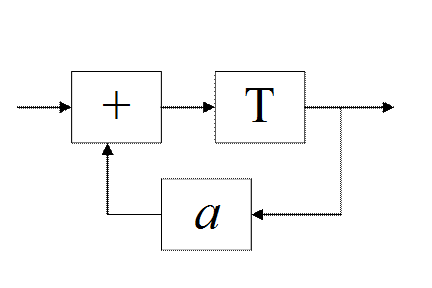
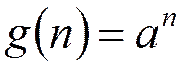
Сигнал на выходе фильтра:
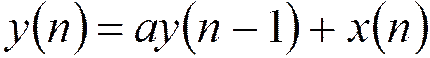
Сигнал на выходе фильтра с учетом шума округления:
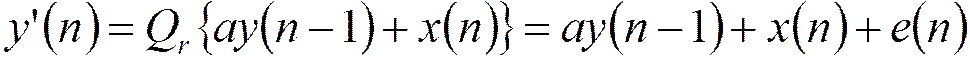 ,
,
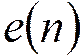 - шум
округления
- шум
округления
Дисперсия выходного шума округления для операций с фиксированной точкой:
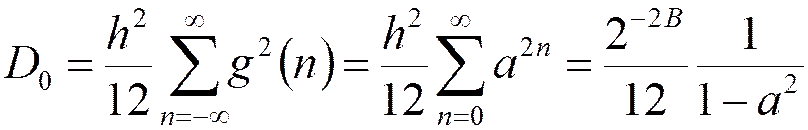
Переполнение разрядной сетки сумматора
Передаточная функция БИХ фильтра 1-го порядка:
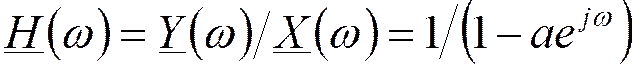
Максимальный коэффициент передачи
фильтра равен: 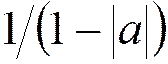
Условие отсутствия переполнения
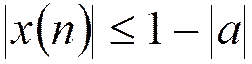
Поэтому входной сигнал представим в виде шума, распределенного на интервале
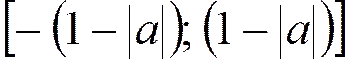
Дисперсия входного шумового сигнала 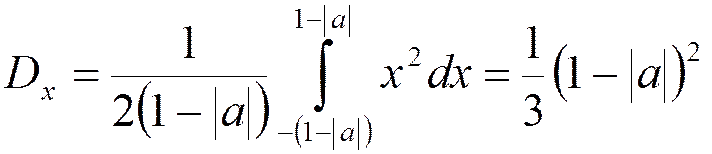
Дисперсия выходного шумового сигнала
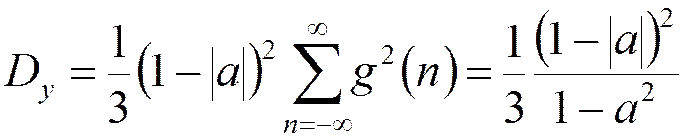
Отношение шум-сигнал на выходе фильтра с фиксированной точкой:
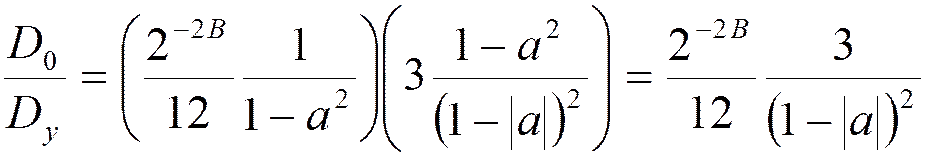
Следует отметить, что отношение
шум-сигнал стремится к бесконечности при уменьшении полосы пропускания
фильтра: 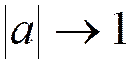 .
.
Шум округления в БИХ-фильтрах с плавающей точкой
Сигнал на выходе БИХ фильтра с плавающей точкой с учетом шума округления:
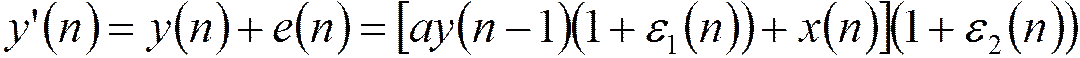
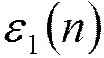 -
ошибка умножения
-
ошибка умножения
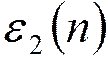 -
ошибка сложения
-
ошибка сложения
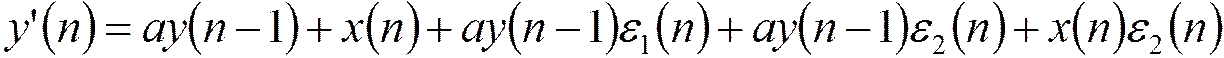
Ошибка округления:
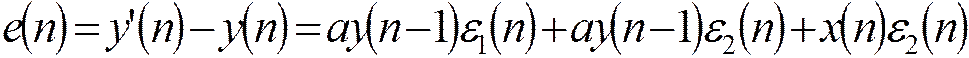
Дисперсия ошибки округления:
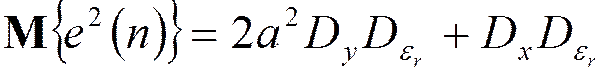 ,
,
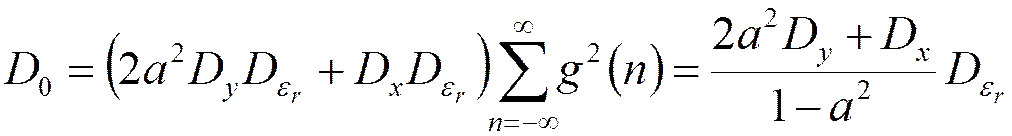 .
.
Дисперсия шумов округления для БИХ фильтра 1-го порядка:
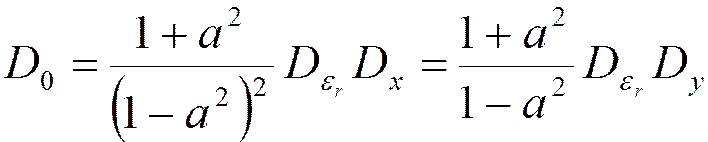
Отношение шум-сигнал на выходе БИХ фильтра 1-го порядка:
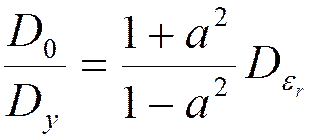
Отношение шум-сигнал на выходе БИХ фильтра 2-го порядка
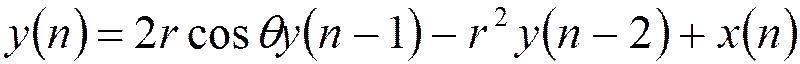
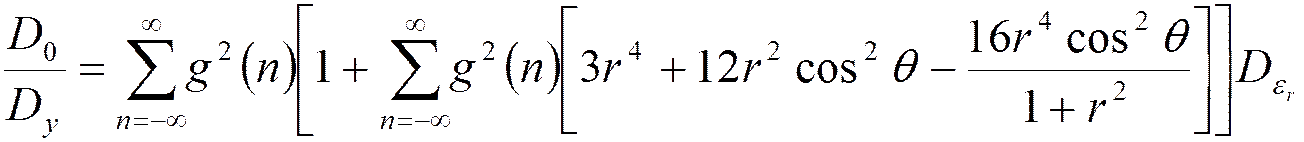
Предельные циклы в цифровых фильтрах
Разностное уравнение для рекурсивного фильтра 1-го порядка:
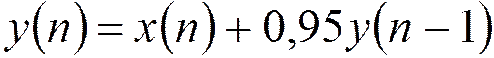
Полюс передаточной функции 0,95, находится внутри единичной окружности, что говорит об устойчивости фильтра.
Пусть входной сигнал
отсутствует, а внутреннее состояние фильтра представляется единственным числом 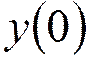 =13.
=13.
При точных вычислениях сигнал на выходе фильтра экспоненциально затухает:
у(1)=12,35; у(2)=11,733; y(3)=11,1459; y(4)=10,588581; y(5)=10,059152; ….
В случае целочисленного представления данных в нутрии фильтра:
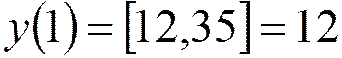 ;
;  ;
; 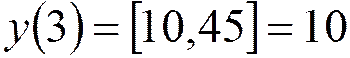 ;
; 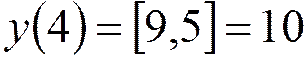 ;
; 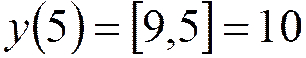
При этом выходной сигнал
остается постоянным 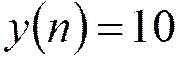 при
при ![]() →
предельный цикл с периодом 1.
→
предельный цикл с периодом 1.
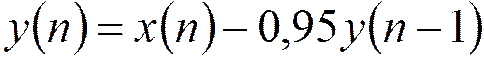
→ получим предельный цикл с периодом, равным двум, в виде чередования значений 10 и -10.
Различают две разновидности предельных циклов:
- «зернистые» (granular) предельные циклы возникают, когда значения внутреннего состояния фильтра при отсутствии входного сигнала затухают, но из-за ошибок округления не доходят до нуля, как в рассмотренном примере,
- «переполняющие» (overflow) предельные циклы имеют место в том случае, когда из-за вычислительных погрешностей значения внутреннего состояния фильтра при отсутствии входного сигнала не затухают, а возрастают, вызывая переполнение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.