Построение статистической модели производственного межфакторного процесса по данным эксперимента 2К, оценка его эффективности при разных законах распределения показателя качества, страница 3

       Коэффициенты Вi уравнения регрессии в табл.1.3 вычисляем по формуле:

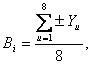
то есть для подсчета любого коэффициента столбцу Y следует приписать знаки соответствующего столбца Хi, сложить значения обобщенного параметра оптимизации с учетом их знаков и результат разделить на число опытов матрицы планирования.

            В результате расчета коэффициентов уравнения регрессии для обобщенного параметра оптимизации получаем уравнение:

Y = 74,25-4,25X₁ –3,5X₂ –4,5X₃ –3,5X₁X₂ – 0,5X₁X₃ + 2,25X₂X₃ + 1,75X₁X₂X₃.

Для проверки зависимости коэффициентов этого уравнения выполняем четыре параллельных опыта на основном уровне (табл.1.2, опыты 9-12).

1.2.  Статистическая обработка результатов.

1.2.1.  Расчет дисперсии параметра оптимизации и доверительного интервала для коэффициентов уравнения.

По параллельным опытам (9-12 в задании) подсчитываем дисперсию параметра оптимизации, доверительный интервал для коэффициентов уравнения.

Дисперсию параметра оптимизации вычисляем по формуле:

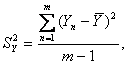
где:     m – число опытов на основном уровне, равное 4;

            Y_n – значение Y, получаемое в каждом из четырех параллельных опытов;

      - среднее арифметическое значение Y.

      Значение , подсчитанное по результатам опытов 9-12, равно 3,333*10^-3.

            Доверительный интервал для коэффициентов регрессии определяем по формуле:

           

            где:     t – критерий Стьюдента;

                        α – уровень значимости;

                         - дисперсия, характеризующая ошибку в определении                                                                      коэффициентов.

            Значение  определяем по формуле:

           

где:      - дисперсия параметра оптимизации;

             N – число опытов матрицы.

Подставляя в эту формулу значения  =3,333*10^-3  и N = 8, получаем

              = 4,166*10^-4

Тогда доверительный интервал коэффициентов уравнения равен:

            Δb_i = ±3,18·√4,166*10^-4  = ±0,065.

Величину t = 3,18 (при α = 0,05 и f = m -1 = 3) выбираем из таблицы.

            Все абсолютные величины коэффициентов регрессии больше доверительного интервала, и поэтому они являются статистически значимыми.

            Для проверки гипотезы адекватности модели уберем наименьший по модулю  коэффициент регрессии. Тогда уравнение будет иметь вид:

      Y = 74,25-4,25X₁ –3,5X₂ –4,5X₃ –3,5X₁X₂ + 2,25X₂X₃ + 1,75X₁X₂X₃

1.2.2.  Расчет дисперсии адекватности.

Для проверки гипотезы адекватности модели, представленной уравнением, находим дисперсию адекватности:

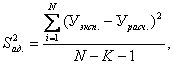
где:     У_эксп. – значение, рассчитанное по экспериментальным данным;