











Лабораторная работа №1.
«Исследование прямого пуска двигателя независимого возбуждения на ЭВМ»
Безреостатный (прямой) пуск двигателя постоянного тока является важнейшим режимом работы двигателей постоянного тока. Он представляет собой сложный электромеханический процесс, сопровождающийся большими всплесками тока в обмотке якоря, резким изменением скорости и, как следствие этого, возникновением высоких механических нагрузок, ухудшением коммутации и теплового состояния машины Указанные обстоятельства ограничивают применение прямого пуска в машинах мощностью до 30 кВт. Наиболее благоприятные условия возникают в случае подачи напряжения на обмотку якоря после того, как ток возбуждения достигнет установившегося значения, при этом упрощается и процесс математического решения переходного процесса.
Другим обстоятельством, определяющим важность изучение прямого пуска, является его непосредственная связь с обеспечением электромеханического быстродействия, электрической машины как элемента электромеханической системы. Электромеханическое быстродействие определяется электромагнитной и электромеханической постоянными времени, пусковым моментом, пусковым током и энергетическими возможностями источника питания.
Математическое описание процесса.
Расчетная схема ДПТ при пуске показана на рис.1. Математическая модель получена при следующих допущениях:
1)
|
2) щетки установлены на геометрической нейтрале, поперечная и коммутационная реакции якоря отсутствуют в течение всего переходного процесса, величина магнитного потока остается неизменной;
3) индуктивность
- ![]() и сопротивление якорной цепи -
и сопротивление якорной цепи - ![]() постоянны;
постоянны;
4) ток
возбуждения много меньше тока якоря, поэтому считать - ![]() .
.
С учетом этих допущений система уравнений имеет вид:
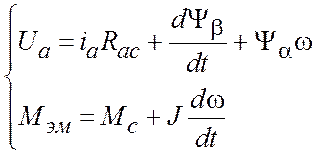 (1)
(1)
![]() ,
, ![]() - напряжение и ток обмотки якоря,
- напряжение и ток обмотки якоря,
![]() - собственное потокосцепление обмотки
якоря по оси β,
- собственное потокосцепление обмотки
якоря по оси β,
![]() - электромагнитный момент.
- электромагнитный момент.
Рассмотрим
решение уравнений (1) для общего случая пуска нагруженного двигателя постоянным
моментом (![]() =Const).
=Const).
Процесс пуска можно представить из двух этапов:
1) в
интервале от t=0 до ![]()
![]() ротор остаётся неподвижным, а ток обмотки
якоря нарастает до значения
ротор остаётся неподвижным, а ток обмотки
якоря нарастает до значения ![]() , при котором
электромагнитный момент достигает момента сопротивления нагрузки;
, при котором
электромагнитный момент достигает момента сопротивления нагрузки;
2) при
времени ![]() >
> ![]() , происходит разгон двигателя.
, происходит разгон двигателя.
Решение на первом этапе.
Так как двигатель на первом этапе неподвижен, то в системе уравнений (1) остается только первое уравнение, в котором отсутствует э.д.с. вращения
![]()
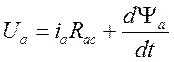 .
.
С учетом
нулевого начального условия, переход к операторной форме уравнения (2),
осуществляется заменой символа дифференцирования ![]() оператором
p.
оператором
p.
![]() или
или ![]()
Последнее выражение дает возможность определить изображение тока
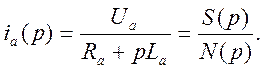
Переход к оригиналу тока осуществляется с помощью теоремы разложения
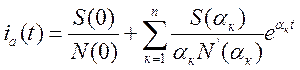 , (2)
, (2)
где S(0) и N(0) – значения
полиномов S(p) и N(p) при p=0; ![]() - корень уравнения N(p) = 0;
- корень уравнения N(p) = 0; ![]() - значение производной полинома N(p) по p при p =
- значение производной полинома N(p) по p при p = ![]() .
.
В результате ток якоря на первом этапе будет изменяться по закону
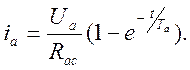 (3)
(3)
Первый этап
заканчивается при достижении током якоря значения, при котором электромагнитный
момент сравняется с моментом нагрузки, следовательно, ток якоря в момент
трогания будет равен ![]() . Подставляя это значение тока в
формулу (2) находим время трогания
. Подставляя это значение тока в
формулу (2) находим время трогания
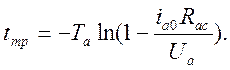
С этого момента
начинается второй этап пуска, начальными условиями, для которого будут ![]() и
и ![]() .
.
Решение на втором этапе.
Переход к операторной форме уравнений (1) следует выполнять с учетом не нулевых начальных условий для тока по выражению
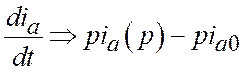 .
.
С учетом этого преобразуем систему (1) к операторному виду и представим ее в матричной форме
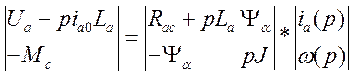 (4)
(4)
Решая систему (4) как алгебраическую, получим изображения тока и скорость в виде:
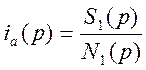 и
и 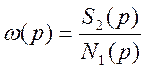 .
.
Переход к оригиналам тока и скорости осуществляется
по выражению (2), учитывая, что ![]() - это корни уравнения
- это корни уравнения ![]() .
.
В результате получаютсятся выражения вида:
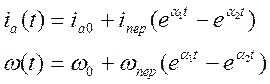 (5)
(5)
Анализ выражений (5) показывает, что в зависимости
от корней характеристического уравнения системы (4), переходный процесс может
быть апериодическим для случая вещественных корней и колебательным для
комплексных сопряженных корней. При этом отрицательным вещественным корням и
комплексным корням с отрицательными вещественными частями соответствует
затухающий во времени переходный процесс. Из характеристического уравнения
системы ![]() получается выражение для корней:
получается выражение для корней:
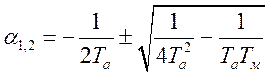 (6)
(6)
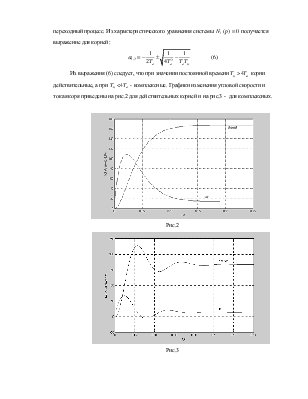
Из выражения (6) следует, что при значении
постоянной времени![]() >
>![]() корни
действительные, а при
корни
действительные, а при ![]() <4
<4![]() -
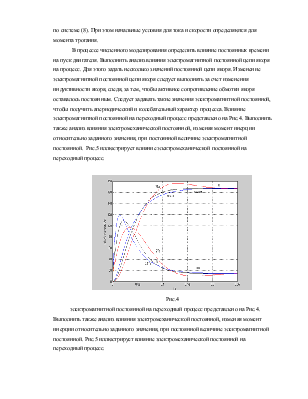
комплексные. Графики изменения угловой скорости и тока якоря приведены на рис.2
для действительных корней и на рис.3 - для комплексных.
-
комплексные. Графики изменения угловой скорости и тока якоря приведены на рис.2
для действительных корней и на рис.3 - для комплексных.
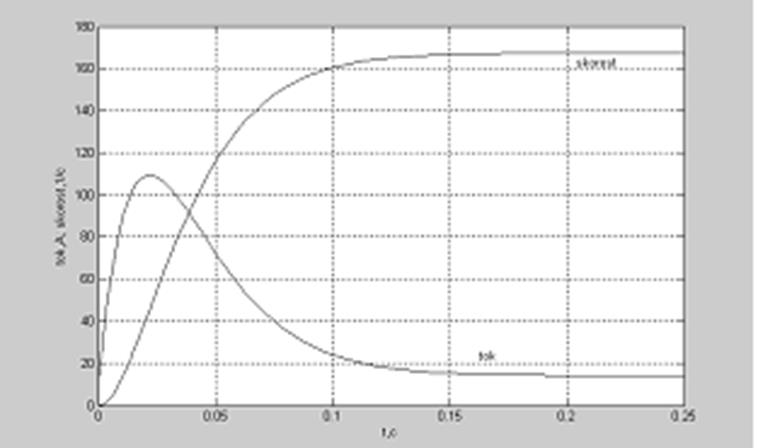
Рис.2
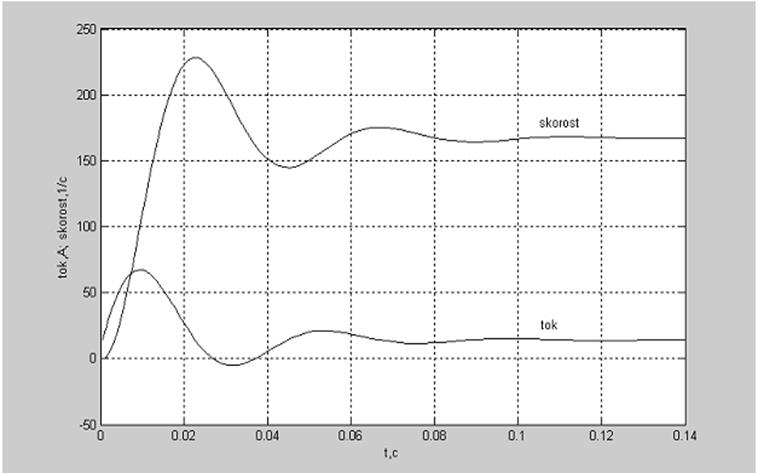
Рис.3
Лабораторная работа №1.
«Исследование прямого пуска двигателя независимого возбуждения на ЭВМ»
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.