
12 ПОМЕХОУСТОЙЧИВОСТЬ НЕПРЕРЫВНЫХ СИГНАЛОВ С ШИРОКОПОЛОСНЫМИ ВИДАМИ МОДУЛЯЦИИ
Обычно для определения помехоустойчивости приема непрерывных сигналов вычисляется отношение средних мощностей сигнала и помехи на выходе демодулятора: ρвых = Рс.вых/Рп.вых. В общем случае помехоустойчивость систем передачи непрерывных сообщений удобно оценивать выигрышем.
Выигрыш демодулятора. В любом демодуляторе отношение сигнал – помеха на выходе зависит не только от качественных показателей демодулятора, но и от отношения сигнал – помеха на его входе. Чем меньше помех на входе, тем меньше их и на выходе, именно поэтому помехоустойчивость удобно оценивать выигрышем в отношении сигнал – помеха (ОСП):
![]()
причем средние мощности помехи на входе Рп.вх и выходе Рп.вых демодулятора определяются в полосе частот соответствующих сигналов.
Выигрыш gс.-п. показывает изменение отношения сигнал – помеха демодулятором. При gс.-п>1 демодулятор улучшает отношение сигнал – помеха, при gс.-п<1 получается проигрыш.
Расчетные формулы выигрыша оптимального демодулятора для различных видов модуляции при помехе в виде аддитивного белого гауссовского шума приведены в табл
В широкополосных системах модуляции (ЧМ, ФМ, ФИМ и др.) выигрыш может быть намного больше единицы и резко возрастает при расширении спектра модулированного сигнала, так как у этих систем кубическая зависимость выигрыша от коэффициента расширения полосы α. Поэтому для увеличения выигрыша следует повышать девиацию частоты угловой модуляции (фазовой и частотной) или уменьшать длительность импульса несущей импульсных видов модуляции. Значительный выигрыш в широкополосных системах модуляции объясняется в основном когерентным сложением в демодуляторе спектральных составляющих сигнала при некогерентном сложении составляющих помех.
|
Вид модуляции |
Выигрыш |
Вид модуляции |
Выигрыш |
|
АМ |
|
ЧМ |
|
|
БМ |
|
ФМ |
|
|
ОМ |
|
АИМ-АМ |
|
|
АИМ |
|
ФИМ-АМ |
|
Обозначения в табл. α = ∆fs/Fm - коэффициент расширения полосы, показывает, во сколько раз ширина спектра модулированного сигнала ∆fs превышает максимальную частоту модулирующего сигнала Fm; m – индекс модуляции; П- пик фактор
![]()
![]()
![]()
![]()
Все широкополосные системы модуляции обеспечивают высокую помехоустойчивость при условии, что отношение сигнала к помехе ρвх на входе демодулятора больше некоторого предельного – порогового значения ρвх.пор. При ρвх < ρвх.пор широкополосные системы теряют свои преимущества: резко снижается помехоустойчивость и связь становится практически невозможной. Значение порога помехоустойчивости определяет предельную дальность связи при заданной мощности передатчика. Поэтому важно определить это значение ρвх.пор и установить закон изменения ОСП на выходе приемника (демодулятора) за порогом помехоустойчивости, т.е. при ρвх < ρвх.пор.
Порогом помехоустойчивости демодулятора является минимальное отношение сигнал – помеха на его входе, ниже которого система связи с заданной модуляцией теряет свои преимущества по помехоустойчивости. Именно пороговый эффект ограничивает возможности широкополосных систем модуляции в повышении качества передачи непрерывных сигналов. Это явление иллюстрируется зависимостями ρвых = f(ρвх) для различных демодуляторов (рис). .
Появление порога помехоустойчивости для широкополосных систем связи можно объяснить эффектом подавления сильным сигналом слабого сигнала в детекторе . В надпороговой области сигнал превышает помеху и в детекторе подавляется более слабая помеха. В подпороговой области помеха превышает сигнал и подавляется уже слабый сигнал более сильной помехой. Возникают аномальные выбросы помехи на выходе, резко снижающие качество передачи. Пороговые явления начинают наблюдаться при равенстве пиковых значений сигнала и помехи. При коэффициенте амплитуды помехи П ≈ 3, порог помехоустойчивости ρвх.пор ≈ 10 дБ (см. рис. ).
При синхронном детектировании АМ, БМ, ОМ сигналов пороговый эффект не наблюдается. На рис. этим видам модуляции соответствуют линейные зависимости при любых значениях ρвх.
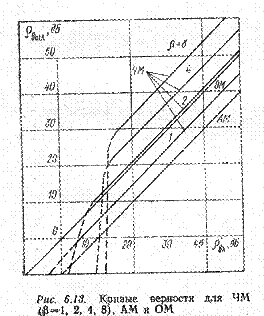 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.