Определение ошибки квантования при напряжении кодируемого сигнала. Определение количества символов ПСП на выходе генератора ПСП. Определение пределов изменения скорости передачи цифрового потока Е на выходе аппаратуры

 Федеральное агентство связи

Хабаровский  институт инфокоммунникаций, филиал

Сибирского государственного университета

телекоммуникации и информатики

КУРСОВАЯ РАБОТА

По дисциплине: Цифровые системы передач

                                               Выполнил:  Студент 3 курса,

Гр. ХС-81 Наумец А.В

Шифр 07021ХА      

                                              Проверил: Емашова Н. П.

г. Хабаровск

 2011 г.

 

Вариант 10.

1.  Спектр модулированного сигнала равен 0,3-3,4 кГц. Определить переходную полосу частот для ФНЧ Δf_ппч, если частота дискретизации выбирается равной F_д=8,6  кГц. Изобразить графически процесс вычисления. Сделать вывод.

Решение:

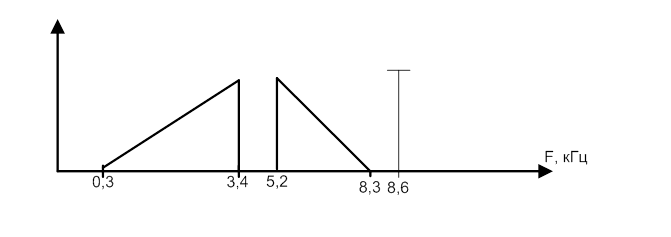
Вывод: при Fд=8,6 кГц не происходит накладывания сигналов, при этом образуется довольно широкая полоса частот Δf_ппч = 1,8 кГц.

2.  Определить ошибку квантования ε(t), при напряжении кодируемого сигнала U=8,1 мВ и мощность шума квантования Р_ш при различных шагах квантования Δ. Сделать вывод.

Δ₁=6,3 мВ, Δ₂=5,3мВ, Δ₃=0,012 мВ.

Решение:

ε=U_АИМ-U_кв;

N_{у кв}=U/Δ;

Р_ш=Δ²/12;

1). Δ=6,3 мВ. N_{у кв}=8,1/6,3=1,28; U=1,28 мВ – ближайший уровень квантования, ;

ε ₀=8,1-6,3*1=8,1-6,3=1,8 мВ.

ε ₁=8,1-6,3*2=8,1-12,6=-4,5 мВ     Р_ш=6,3²/12=3,3 мкВт.

2) ). Δ=5,3 мВ. N_{у кв}=8,1/5,3=1,5;

ε =8,1-5,3*2=8,1-10,6=-2,5 мВ

Р_ш=5,3²/12=2,34 мкВт.

3) Δ=0,012 мВ. N_{у кв}=8,1/0,012=675;

Р_ш=0,012²/12=0,000012 мкВт.

Ответ: ε₁=1,8 мВ; ε₂=-2,5 мВ;  Р_ш1=3,3 мкВт; Р_ш2=2,34 мкВт; Р_ш3=0,000012 мкВт;

Вывод: чем меньше шаг квантования, тем меньше ошибка квантования.

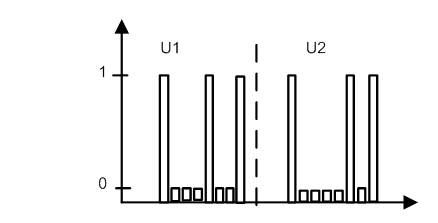
3.  Даны уровни АИМ сигналов U1(t) и U2(t), В. Необходимо иллюстрировать этапы преобразования этих сигналов в кодовую комбинацию на выходе линейного кодера при двух шагах квантования Δ1 и Δ2 тремя графиками:

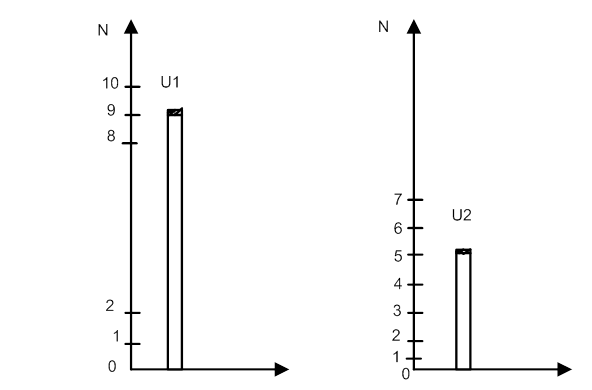
1.  График квантованных значений U1кв(t) и U2кв(t), нумерация уровней квантования;

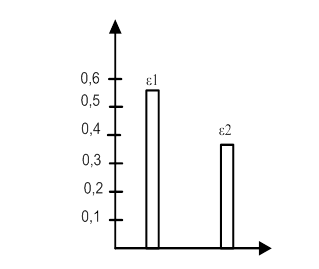
2.  График ошибок квантования;

3.  График преобразования десятичных значений уровня квантования в двоичное число.

Представить указанные преобразования в виде таблицы при двух шагах квантования.

U₁=4,58 B; U₂=8,37 B; Δ₁=0,5; Δ₂=1,6;

Решение:

U₁=4,58 B; U₂=8,37 B; Δ₁=0,5; Δ₂=1,6;

1). Δ₁=0,5; при N=9, U₁=4,58;

Uкв=4 В; N=10001001. ε₁=0,58 В.

2). Δ₂=1,6; при N=5 U₂=8,37,

Uкв=8 B; N=10000101, ε₂=0,37 B.

Отсчет сигнала	UАИМ  (t) B	Uкв (t)	ε(t)	εmax (t)	N	Двоичный код уровня квантования
1	4,58	4	0,58	0,25	9	10001001
2	8,37	8	0,37	0,8	5	10000101

4.  На вход преобразователя кода линейного декодера поступает 8-разрядная кодовая группа ИКМ сигнала к. к. Определить амплитуду закодированного отсчета АИМ сигнала, если шаг квантования Δ=3,7 мВ.

Кк₁=01100110, кк₂=00100001, кк₃=01101010;

Решение:

Кк₁=01100110, кк₂=00100001, кк₃=01101010;

N₁= -(64+32+4+2)=-102;        U₁=N₁*Δ=-102*3,7=-377,4 мВ;

N₂=-(32+1)=-33;                     U₂=-33*3,7=-122,1 мВ;

N₃=-(64+32+8+2)=106;           U₃=-106*3,7=-392,2 мВ;

Ответ: U₁=-377,4 мВ, U₂=-122,1 мВ, U₃=-392,2 мВ.

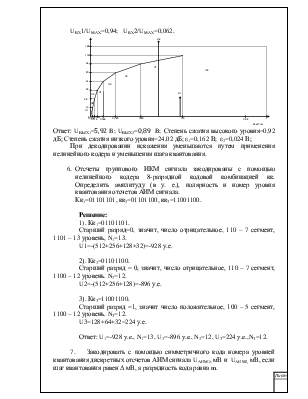
5.  На нелинейный кодер с амплитудной характеристикой компрессии типа А-87,6/13 поступает групповой ИКМ сигнал, амплитуды отсчетов которого соответственно равны U_BX1, [B] и U_BX2[мВ]. Требуется вычислить амплитуды этих сигналов на выходе декодера, при максимальном значении амплитуды U_MAX, [B]. Проверить степени сжатия сигнала  низкого и высокого уровня в дБ. Изобразить графически процесс кодирования U_ВЫХ1, [B] и U_ВЫХ2  [B] на амплитудной характеристике кодера при шаге квантования, равном Δ. Определить ошибку квантования. Каким образом уменьшаются искажения при декодировании?

Δ=0,006; U_BX1=5,60 B; U_BX2=56 мВ;

 U_MAX=6 B.

Решение:

U_вых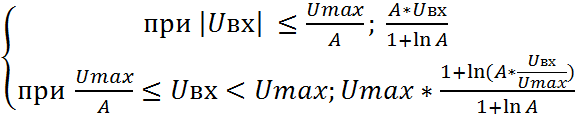

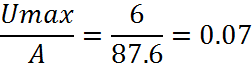
Следовательно

U_вых1=6* =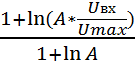

2) Uвх2=56 мВ

 _;

Uвых2=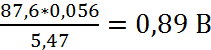

Степень сжатия=20*lg=0,92 дБ;

Степень сжатия=20*lg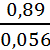=24,02 дБ;

Кодирование сигналов:

Число положительное, значит, старшему разряду присваиваем 1.

U_ВЫХ1_у.е=U_ВЫХ1_у.е./Δ=5,92/0,006=987Δ; U_ВЫХ2_у.е.=0,89/0,006=148Δ;

987Δ-256Δ=731Δ;

987Δ-512Δ=475Δ;

987Δ-1024Δ=-37Δ;

Основным эталонным сигналом является 512Δ, значит сигнал относится к 7 сегменту.

475Δ-256Δ=219Δ>0; присваиваем 1;

219Δ-128Δ=91Δ>0; присваиваем 1;

91Δ-64Δ=27Δ>0; присваиваем 1;

27Δ-32Δ=-5Δ<0; присваиваем 0;

ε1=27Δ=0,162 В;  U_ВЫХ1=11101110 – 7 сегмент, 13 уровень;

Разница: 987- (512+256+128+64)=27

U_ВЫХ2=148Δ;

Число положительное, значит, присваиваем старшему разряду 1.

148Δ-128Δ=20Δ>0;

148Δ-256Δ=-108<0;

Основным эталонным сигналом является 128Δ, значит сигнал принадлежит 5 сегменту.

20Δ-64Δ=-44Δ<0, присваиваем 0;

20Δ-32Δ=-12Δ<0, присваиваем 0;

20Δ-16Δ=4Δ>0, присваиваем 1;