Из вентилей анодной группы (VD4, VD6, VD2), имеющих одинаковый потенциал на анодах, в данный момент времени откроется тот, у которого потенциал на катоде будет максимальный по величине и отрицательный по знаку (рис. 24, б). Потенциал общего анода схемы (точка Р на рис. 24, а) будет представлять кривую, огибающую отрицательные участки синусоидальных фазных напряжений (кривая Р на рис. 24, б). Таким образом, в мостовой схеме всегда (при Хв = 0) открыто два вентиля и ток проходит по двум фазам вторичной обмотки, двум вентилям и нагрузке. Все перечисленные элементы включены в контур протекания тока последовательно и iVD = i2 = Id.
Пару вентилей, находящихся в проводящем состоянии, определить легко – она находится под наибольшим междуфазным (линейным) напряжением. За период питающего напряжения возможно шесть интервалов повторяемости, в каждом из которых открыто два вентиля (рис. 24, в, г).
Из схемы выпрямителя (рис. 24, а) ясно, что мгновенные значения напряжения на нагрузке равны разности потенциалов в точках К и Р. Выше отмечалось, что открытые вентили подключают в эти точки те или иные фазы. Следовательно, кривая выпрямленного напряжения ud представляет собой разность фазных или линейное напряжение ud = u2 лин. Кривая ud имеет шесть пульсаций за период питающего напряжения при амплитуде пульсации равной максимальному линейному напряжению (рис. 24, б).
То обстоятельство, что мостовая схема выпрямляет линейное, а не фазное, как в нулевых схемах, напряжение – обусловливает основные ее достоинства.
Среднее значение выпрямленного напряжения при холостом ходе выпрямителя (рис. 24, б) определится так:
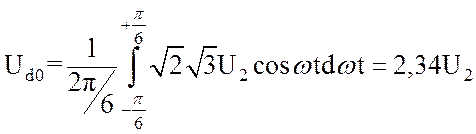, (88)
и, соответственно,
.
В этих выражениях
проявляются достоинства схемы: имея всего m2 = 3, получено m = 6 (в нулевых
схемах необходимо m2 = 6) при вдвое меньшем числе витков
на фазу (в предыдущих схемах 
).
Условия работы вентилей в этой схеме определяются следующими значениями токов (рис. 24, в, г):
– максимальное значение тока вентильного плеча IVD max = Id;
– среднее значение тока вентильного плеча IVD ср = Id / 3.
Условия работы вентилей в этой схеме также определяются значением максимального обратного напряжения на вентильном плече. Кривая обратного напряжения на вентильном плече в этой схеме представлена на рис. 24, ж. Максимальное значение обратного напряжения определяется его амплитудой:
UVD max = 
= 1,045 Ud0. (89)
Анализ условий работы вентилей показывает, что токовый режим работы вентилей в два раза тяжелее, чем в нулевой шестипульсовой схеме параллельного типа и, следовательно, число параллельных вентилей в вентильном плече в этой схеме будет вдвое больше. Режим напряжения наоборот в два раза легче и требуется вдвое меньшее число последовательно соединенных вентилей. Таким образом, общее число полупроводниковых вентилей в шести вентильных плечах этой схемы будет таким же, что и в других шестипульсовых схемах выпрямления.
Достоинства или недостатки схемы в этих условиях определяются сравнением трансформаторов. Ток вторичной обмотки шестипульсовой мостовой схемы разомкнутого типа (ia на рис. 24, а) по закону Кирхгофа определится как
iа + iVD4 – iVD1 = 0, (90)
откуда
iа = iVD1 – iVD4. (91)
Кривая тока вентильной обмотки трансформатора в этой схеме, построенная по выражению (91), приведена на рис. 24, д. Диаграмма тока подчеркивает, что фаза обмотки обтекается током в двух направлениях (в два такта) продолжительностью 4π/3. Это естественно улучшает использование обмоток трансформатора.
Действующее значение тока вентильной обмотки трансформатора равно:
.
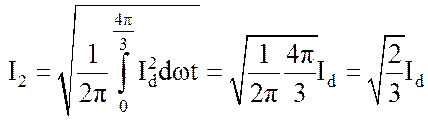(92)
Для рассматриваемой схемы справедливо
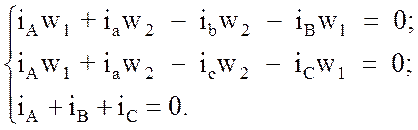(93)
Решение этой системы
уравнений с учетом, что 
, дает 
(рис. 24, и).
Следовательно
.
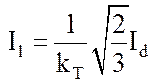(94)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.