4. Банкетным сечением устраняются недостатки сжатых и вытянутых форм. Применяется при значительных колебаниях расходов стоков.
5. Открытые сечения каналов (11, 12) могут применяться за пределами населенного пункта и на очистных сооружениях канализации.
Гидравлически выгодным является прямоугольное сечение
при b/h = 2 и трапециидальное сечение при b/h = 2(![]() ), где m = ctg
), где m = ctg![]() .
.
3.4. Зависимость расхода и скорости от степени наполнения трубопровода
Рис. 18. Графическая иллюстрация связи расхода и скорости от наполнения сточных вод
Максимальная скорость при h/d = 0,813, а максимальный расход при h/d = 0,95.
Расход при h/d = 1 в 2 раза больше расхода при h/d = 0,5. Существует область, где одинаковые скорости и расходы достигаются при двух разных наполнениях, а скорость при h/d = 0,5 равна скорости при h/d = 1.
Для городских сетей рекомендуется принимать h/d = 0,5 – 0,8, а для водосточной сети h/d = 0,95 – 1,0. В СНИП 2.04.03-85 приводятся следующие максимальные наполнения трубопроводов.
D,мм h/d
150-300 0,6
350-450 0,7
500-900 0,75
Более 900 0,8
3.5. Гидравлический расчет самотечных трубопроводов
Гидравлический расчет самотечных трубопроводов сводится к определению d, i, h/d, v при известном расходе ст. вод для установившегося и равномерного движения. Гидравлический расчет производится с учетом технико-экономических показателей проектирования и строительства и др. условий.
В настоящее время предлагается две методики гидравлического расчета. Первая методика справедлива для области вполне шероховатого трения турбулентного режима.
Вторая методика применяется для всех трех областей турбулентного режима: гладких труб, вполне шероховатых и в переходной области между ними. Так как водоотводящие сети в основном работают в области вполне шероховатого трения, то результаты расчета по обеим методикам получаются практически одинаковыми.
Первая методика
1. Формула постоянства расхода
q = Q * v
2. Формула Шези (справедлива для всех сечений труб и коллекторов за счет применения R вместо D)
v = С ![]()
3. Коэффициент Шези (формула Павловского Н. Н. справедлива для области вполне шероховатого трения и 0,1 < R < 3).
С = (Rу)/n.
y = 2,5 n– 0,75 R ( n – 0,1) – 0,13.
При 0,1 < R < 1 у ~ 1,5 n
1 < R < 3 у ~ 1,3 n
Известна формула Маннинга для определения С, где у = 1/6.
![]() –
площадь живого сечения потока;
–
площадь живого сечения потока;
v – средняя скорость движения воды;
R – гидравлический радиус,
R = ![]() /
/![]() ,
,
![]() (капа)
– смоченный периметр сечения коллектора;
(капа)
– смоченный периметр сечения коллектора;
i – уклон лотка, равный гидравлическому уклону при равномерном движении, где
![]()
![]()
![]()
![]()
|
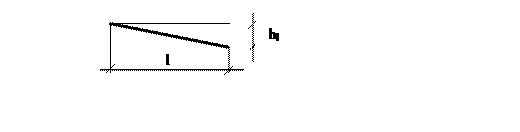
n – коэффициент шероховатости, зависит от состояния стенок русла n = 0,012 – 0,015 для коллекторов и труб и 0,02 – 0,03 – для земляного русла.
Вторая методика
1.
q = ![]() * v
* v
2. Формула Дарси
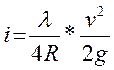
3. Формула Н. Ф. Федорова ( справедлива для всех трех областей турбулентного
режима)
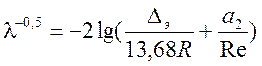
![]() - коэффициент гидравлического трения;
- коэффициент гидравлического трения;
![]() э –
эквивалентная абсолютная шероховатость, зависит от поверхности трубопроводов
(материала труб),
э –
эквивалентная абсолютная шероховатость, зависит от поверхности трубопроводов
(материала труб), ![]() =
0,005(полипропилен) – 3,0(бетонные и ж/б каналы) [Алексеев, Карамзинов,
Курганов и др.];
=
0,005(полипропилен) – 3,0(бетонные и ж/б каналы) [Алексеев, Карамзинов,
Курганов и др.];
а2 – коэффициент, учитывающий характер шероховатости труб (зависит от материала труб); а2 = 20 – 130 [табл. 3.5, Алексеев, Карамзинов, Курганов];
Re – число Рейнольдса
Re = (4R*v)/![]() ,
,
![]() - кинематический коэффициент вязкости.
- кинематический коэффициент вязкости.
Обе методики связаны соотношением
С = (8g/![]() )0,5 или С2 = 8g/
)0,5 или С2 = 8g/![]() ,
,
с помощью которого формула Дарси превращается в формулу Шези. По первой методике рассчитаны таблицы Лукиных, по второй – таблицы Федорова Н. Ф., Волкова Л. Е. (Гидравлический расчет канализационных сетей. Стройиздат. 1968.)
Для расчёта гидравлического радиуса R и
площади живого сечения ![]() применяются
тригонометрические функции в зависимости от наполнения h/d.
применяются
тригонометрические функции в зависимости от наполнения h/d.
Рис. 19. Геометрические параметры потока
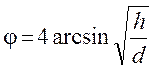 , рад
, рад
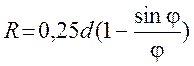 ;
;
![]() ;
;
Ширина поверхности воды в трубопроводе:
В = 2d![]()
Местные потери напора – по формуле Вейсбаха
hм = ![]() v2/2g,
v2/2g,
где ![]() -коэффициент местного сопротивления
(приводится в справочной литературе).
-коэффициент местного сопротивления
(приводится в справочной литературе).
Минимальная, самоочищающая или незаиливающая скорость определяется по формуле Н. Ф. Федорова:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.