Устройство для управления системой очистки лобового стекла автомобиля, страница 23

0850  A7 C2 4C 08 0D C2 4E 08 7B CD 89 08 3E 0D D3 80

0860  CD 89 08 3E 61 D3 80 15 C2 3C 08 CD 89 08 3E 0C

0870  D3 80 CD 89 08 3E 60 D3 80 15 C2 3C 08 C3 3A 08

0880  7A EE 01 57 D3 80 C3 0D 08 01 29 8E E6 00 DB 82

0890  5F 0B 79 B0 CA BE 08 7B E6 01 CA 8E 08 0E FA DB

08A0  82 E6 01 CA 8E 08 0D C2 9F 08 DB 82 5F 0E FA DB

08B0  82 A7 C2 AD 08 0D C2 AF 08 7B E1 C3 07 08 C9

Количество байт - 191

Начальный адрес - 0800

Конечный адрес  - 08BE

Контрольная сумма - 0D

Для полноценного понимания текста программы приведем систему команд для данного типа микропроцессора (рисунок 13).

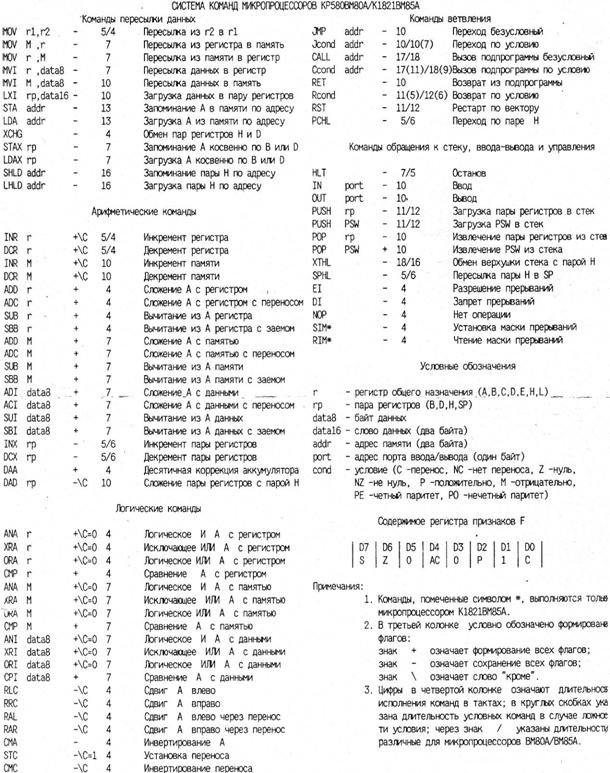
Рисунок 13 – Система команд микропроцессоров КР580ВМ80А/К1821ВМ85А
3 Оценка цикломатического числа Маккейба и безошибочности программы

Маккейбом предложено метрикой сложности считать цикломатическую сложность графа программы, характеризующую трудоемкость тестирования программы.

Для вычисления цикломатического числа Маккейба применяется формула:

                                                                                       (1)

где e – число дуг ориентированного графа;

w – число вершин;

p – число компонентов связанности графа.

Число компонентов связанности графа можно рассматривать, как количество дуг, которые необходимо добавить для преобразования графа в сильносвязный. Сильносвязным называется граф, любые две вершины которого взаимно достижимы. Для графов корректных программ, то есть графов, не имеющих недостижимых от точки входа участков и «висячих» точек входа и выхода, сильносвязный граф, как правило, получается путем замыкания другой вершины, обозначающей конец программы, на вершину, обозначающую точку входа в эту программу (рисунок 13).

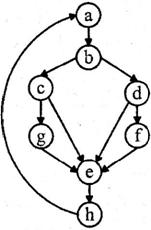
Рисунок 13 – Сильносвязный граф

Таким образом, цикломатическое число Маккейба показывает количество тестовых прогонов программы, необходимых для исчерпывающего тестирования по критерию «работает каждая ветвь».

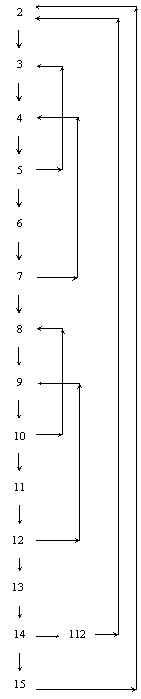
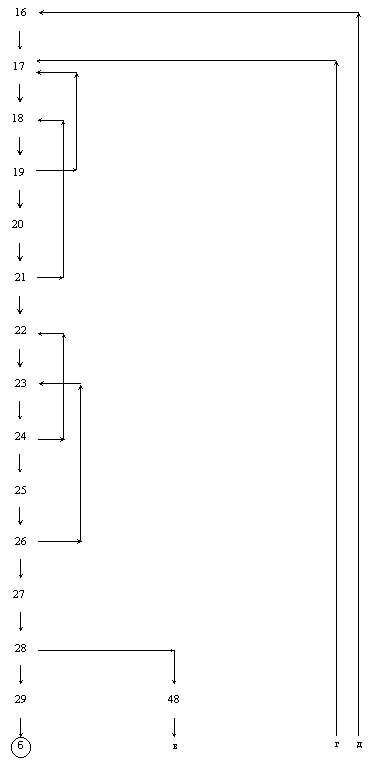
Для оценки качества разработанного алгоритма и программы составим граф (рисунок 14), линейные участки которого сведены к одной вершине.