Расчёты по растяжению-сжатию, страница 2

Найдём напряжения:

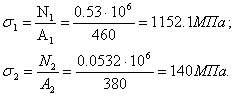
Силовые деформации стержней равны:

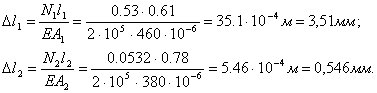
Тогда изменение длины стержней будет равно:

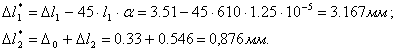
Т.к. мы получили положительные значения абсолютных изменений длин стержней, то это свидетельствует о правильно выбранной схеме деформации, т.е. стержни удлиняются.
Задание №1.4

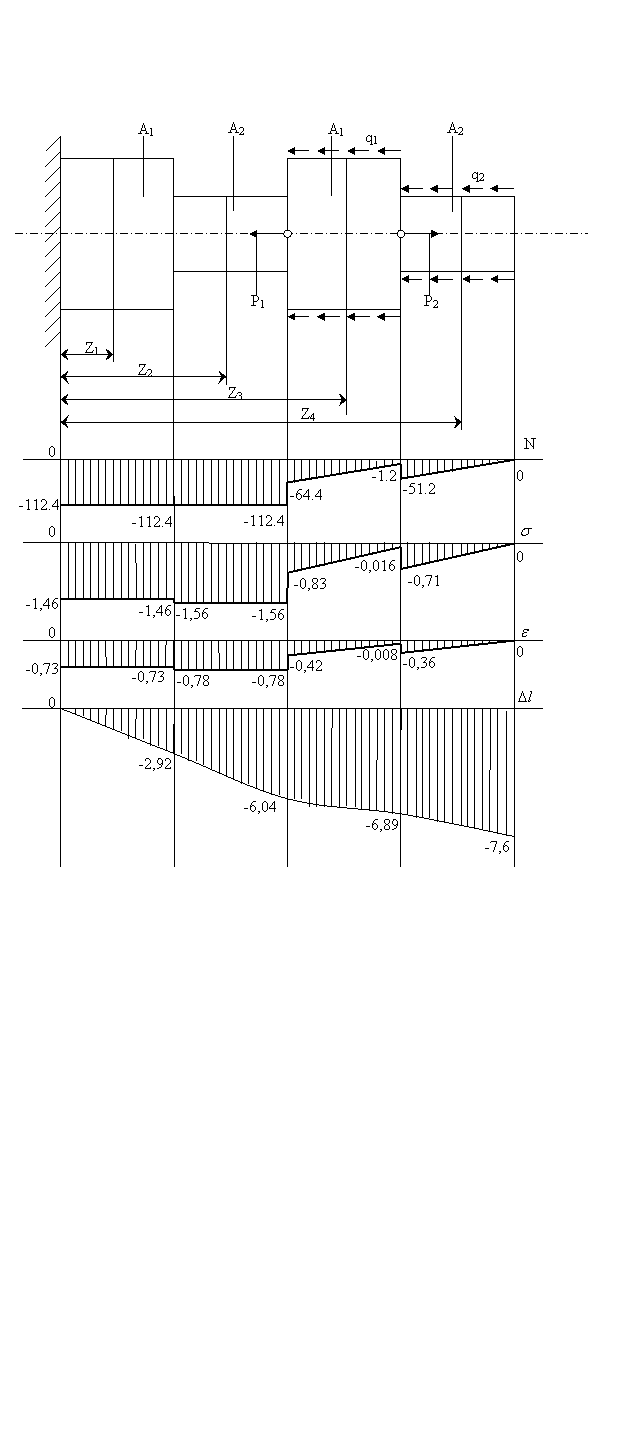
Дана схеме:

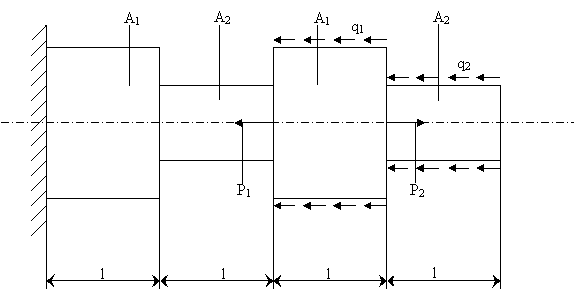
Дано: P₁=48кН, P₂=50кН, А₁=77мм², А₂=72мм², l=0.4мм, q₁=158кН/м, q₂=128кН/м, Е=2*10⁵МПа.

Решение: Решаем уравнение перемещения относительно R_A:

1)R_A-q₁l-q₂l-P₁+P₂=0

R_A=q₁l+q₂l+P₁-P₂

R_A=158*0.4+128*0.4+48-50=112.4кН.

Рассматриваем теперь реакцию внешних сил, составим выражение продольных сил на каждом участке и найдём их граничные значения:

2)N₁=-R=-112.4 кН

N₂=-R=-112.4 кН

N₃=-R+q₁(z₃-2l)+P₁=-112.4+158z₃-126.4+48=-190.8+158z₃

N₄=-R+q₁l+P₁-P₂+q₂(z₄-3l)=-112.4

63.2+48-50+128(z₄-1.2)=-204.8+128z₄

N₁(0)=-112.4 кН

N₁(l)=-112.4 кН

N₂(l)=-112.4 кН

N₂(2l)=-112.4 кН

N₃(2l)=-64.4 кН

N₃(3l)=-1.2 кН

N₄(3l)=-51.2 кН

N₄(4l)=0 кН

По найденным граничным значениям строим эпюру N. Рассчитываем нормальные напряжения в граничных сечениях на каждом участке:

 В

 В

 В

 В

 В

 В

 В

По найденным граничным значениям строим эпюру . Рассчитаем относительную деформацию в граничных сечениях на каждом участке.

По данным граничных сечений строим эпюру . Рассчитаем относительное удлинение:

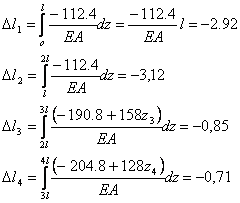
Рассчитаем абсолютное удлинение и построим эпюры:

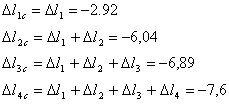
Т.к. все удлинения <0 , то данный брус сжимается.

Т.к. точка экстремума лежит на границе участка (4), то