Астатическая настройка регулятора напряжения (см. рис. 3.21, в). Механическая характеристика на некотором интервале изменения совпадает с одной из электромеханических характеристик. Положение равновесия для любой нагрузки будет соответствовать одному и тому же напряжению, т. е. регулируемое напряжение не зависит от нагрузки, внешняя характеристика генератора с регулятором напряжения параллельна оси абсцисс (см. рис. 3.22, кривая 3). Угольные регуляторы напряжения, как правило, настраивают с небольшим положительным статизмом, так как при такой настройке легче обеспечить устойчивость процесса регулирования.
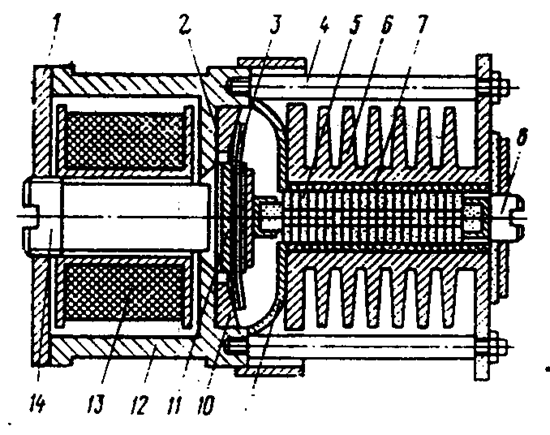
Рис. 3.23. Угольный регулятор напряжения
Угольный регулятор напряжения (рис. 3.23) состоит из угольного столба 5, помещенного в дюралюминиевую трубку 7 с оксидно-лаковым покрытием, укрепленную в ребристом корпусе радиатора 6, электромагнита с сердечником 14 и подвижным якорем 11, укрепленном на пружине 3, регулировочного винта 8. На сердечнике электромагнита расположена обмотка 13. Корпус 12 электромагнита выполнен в виде стакана с крышкой 1. Пружина с якорем опирается на кольцо 10. Для предотвращения прилипания якоря к сердечнику между корпусом электромагнита и опорным кольцом прокладывается диамагнитная (латунная) прокладка 2. Ребристый корпус соединен с корпусом электромагнита стальными винтами 4. Радиатор от электромагнита отделяется теплоизолирующим экраном в виде стального колпака 9.
Динамика работы угольного регулятора напряжения. Переходные процессы в угольном регуляторе напряжения можно представить следующими уравнениями.
1. Уравнение изменения сопротивления угольного столба. Сопротивление угольного столба rс регулятора связано с перемещением якоря х нелинейной зависимостью rc= rс (х).
Приращение сопротивления столба при его деформации
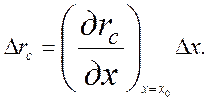
В относительных единицах
![]() (3.7)
(3.7)
где ρc = Δrc/(rb + rc0) — относительное изменение сопротивления угольного столба;
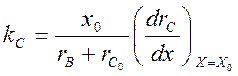 —
коэффициент усиления угольного столба;
—
коэффициент усиления угольного столба;
μ = Δx/x o — относительное изменение расстояния между якорем и сердечником электромагнита.
2. Уравнение движения якоря электромагнита. Уравнение равновесия сил, действующих в процессе движения на якорь электромагнита, имеет вид
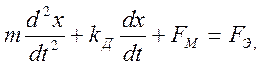 (3.8)
(3.8)
где т — масса подвижных частей, приведенных к центру массы якоря электромагнита; kд — коэффициент демпфирования (вязкого трения); Fm = Fm (x) — механическая сила, равная разности сил сжатия пружины и реакции угольного столба; Fэ = Fэ(х, iэ) — электромагнитная сила.
Уравнение (3.8) в малых приращениях и операторной форме можно представить следующим образом:
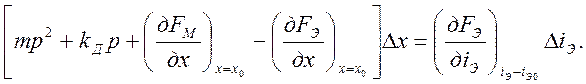 (3.9)
(3.9)
Уравнение в относительных приращениях можно получить, разделив обе части уравнения (3.9) на значение силы Fэ0 = Fм0 в состоянии равновесия и введя обозначения:
Тм = Ö mx0 /Fэ0 — постоянная времени, обусловленная массой якоря;
Тд = kдx0 /Fэ0 — постоянная времени демпфирования угольного столба;
dс = (km — kx)
x0 /Fэ0 — коэффициент, характеризующий настройку регулятора
(при астатической настройке 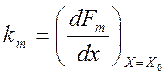 и
и 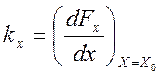 равны, следовательно, dс =0 );
равны, следовательно, dс =0 );
jэ = Δi/i o — относительное изменение тока в обмотке электромагнита;
μ = Δx/x o — относительное изменение расстояния между якорем и сердечником;
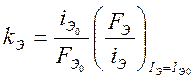 — коэффициент усиления, характеризующий эффективность
электромагнита.
— коэффициент усиления, характеризующий эффективность
электромагнита.
Тогда вместо (3.9) получим уравнение в относительных приращениях:
![]() (3.10)
(3.10)
3. Уравнение цепи рабочей обмотки электромагнита
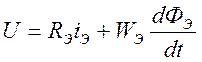 ,
,
где Rэ — сопротивление цепи электромагнита; Wэ — число витков электромагнита; Фэ = Фэ (х, iэ) — магнитный поток, сцепленный с обмоткой электромагнита.
В малых приращениях и операторной форме из (3.11) получим
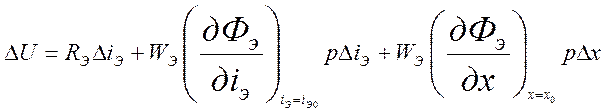 (3.11)
(3.11)
К относительным приращениям можно перейти, разделив члены уравнения (3.12) на равновесное значение U0 = Rэiэ0:
u = jэ + Tэpjэ + Tx pm(3.10)
где 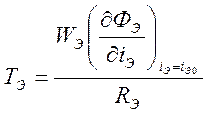 — постоянная времени цепи
электромагнита;
— постоянная времени цепи
электромагнита;
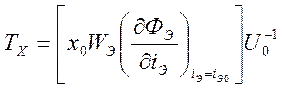 — постоянная времени дополнительного
демпфирования, характеризующая э.д.с., наводимую при движении якоря
электромагнита.
— постоянная времени дополнительного
демпфирования, характеризующая э.д.с., наводимую при движении якоря
электромагнита.
Расчеты и экспериментальные исследования показывают, что величина Tэpjэ << Tx pmи ею можно пренебречь. При этом
u = jэ + Tx pm(3.14)
Объединив уравнения (3.7), (3.10), (3.14), получим уравнение угольного регулятора напряжения
![]() (3.15)
(3.15)
Таким образом, переходные процессы в угольном регуляторе напряжения описываются дифференциальным уравнением второго порядка.
Передаточная функция регулятора
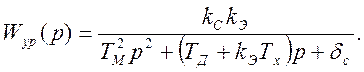 (3.16)
(3.16)
и, следовательно, регулятор является колебательным звеном (корни характеристического уравнения сопряженно-комплексные).
При астатической настройке регулятора (dс = 0) передаточная функция представляет собой последовательное соединение инерционного и интегрирующего звеньев:
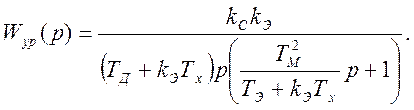 (3.17)
(3.17)
Вопросы для самоконтроля
1. В чем преимущества измерительных органов с двумя стабилитронами?
2. Зависит ли частота переключении исполнительного органа релейного регулятора от частоты вращения генератора?
3. Из каких условий выбирается частота замыканий транзисторного ключа в импульсных регуляторах?
4. Будет ли влиять изменение угловой скорости синхронного генератора на работу фазосдвигающего устройства тиристорного регулятора и почему?
5. Обеспечивается ли астатическая настройка угольного регулятора напряжения для всех возможных режимов работы генератора?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.