Построение плана скоростей. Силовой расчет механизма, страница 2

                                              = =    ,

                                             = =     ,

где   - ускорение стойки D  равно нулю;

- полное ускорение точки В₁ относительно точки D  во вращательном движении звена 3 относительно стойки и равное сумме ускорений   и  ;

  - нормальное ускорение точки В во вращении звена 3 относительно точки D, направленное от точки В₁ к точке D  и по модулю равное:

,

окружное (тангенциальное) ускорение точки В₁ во вращении звена В₁ D относительно точки D и направленное перпендикулярно звену 3;

- полное ускорение точки А₁;

- относительное ускорение точки В₁ звена 3 относительно ведущей точки А₁ звена 1;

-нормальное ускорение т.В1 относительно звена 2, по модулю равное:

и направленное от точки А1 к точке В1 параллельно звену АВ;

- окружное (тангенциальное) ускорение точки В1 относительно точки А1 и направленное перпендикулярно звену АВ.

Определяем длину отрезка изображения ускорения  :  и откладываем из точки а1 этот отрезок

параллельно звену АВ, из его конца перпендикулярно ему проводим линию направления ускорения .

Определяем длину отрезка изображения ускорения :  и откладываем из точки  этот отрезок параллельно звену BD и из его конца перпендикулярно ему проводим линию направления ускорения .

При пересечении линий направлений ускорений  получим точку , соединив ее с точкой , получим отрезок ускорения  на плане скоростей.

Определяем величину этого ускорения: .

          Для построения планов ускорений группы 4 – 5 и определения ускорения точки  запишем 2 векторных уравнения ускорения точки С:

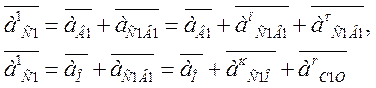
где - полное ускорение точки В определяется из плана скоростей;

- полное ускорение точки  относительно точки  во вращательном движении звена 4 равное сумме ускорений ;

- нормальное ускорение точки С1 во вращении звена относительно точки В1 и направленное от точки С1 к точке В1 и по модулю равное:

;

- касательное ускорение точки С1 относительно точкиВ1 и направленное перпендикулярно звену ВС;

- кориолисово ускорение точки С1 относительно направляющих, равно 0;

- ускорение направляющих, равно 0;

 - относительное ускорение прямолинейного движения точки С1 звена 5 относительно направляющих, направлено параллельно направляющим.

Определяем длину отрезка изображения ускорения :

 и откладываем из точки b1 этот отрезок параллельно звену СВ, из его конца перпендикулярно ему проводим линию направления ускорения .

Т.к. Кориолисово ускорение равно 0 то из полюса  откладываем параллельно направляющим линию направления ускорения.

При пересечении линий направлений ускорений  получим точку С1, соединив ее с точкой  получим отрезок ускорения  на плане скоростей. Определяем величину этого ускорения:

Ускорения середины звеньев 2 и 4 равны:

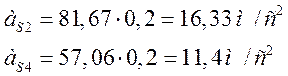
Вычисление ускорений и построение планов ускорений для положений механизма 2 – 11 проводим аналогичным способом.

Угловые ускорения звеньев ВА, ВD, BC определяем из соотношения

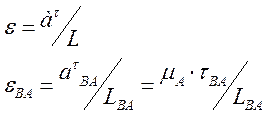, где  длина вектора на плане ускорений

Если вектор  условно перенести в точку А, можно найти направление , они направлены в одну сторону.

, где  - длина вектора  на плане ускорений

.

Если вектор  условно перенести в точку В, можно найти направление , они направлены в одну сторону.

Аналогично находим угловые ускорения в других положениях механизма.

Силовой расчет механизма.

          Составляем уравнение равновесия группы, состоящей из звеньев 4 и 5. Геометрическая сумма сил, приложенных к группе:

на механизм действует одна внешняя сила, приложенная к звену 5 – сила давления в гидроцилиндре Р = 480 Н;

-  сила веса звена 4, приложенная в центре масс звена;

 - сила инерции центра масс звена 4;

- равнодействующая сила реакции в направляющих, направленная перпендикулярно направляющим;

- сила реакции в кинематической паре В, направленная вдоль звена СВ (параллельно линии СВ).

Строим план группы сил 4-5. Выбираем масштаб сил .

От произвольно выбранной точки  откладываем в масштабе силу Р в виде вертикального отрезка , из точки  параллельно ускорению  и в противоположную сторону ему откладываем отрезок ;

из точки вертикально вниз откладываем отрезок ;

через точку  проводим линию, перпендикулярную направляющим (направление силы ), через точку  параллельно ВС проводим направление действия силы  и при их пересечении получаем точку .

Отрезок  дает в масштабе  величину реакции ; отрезок  дает в масштабе  величину реакции .

Проводим построение плана сил группы Асура, образованной звеньями 2 и 3.

Уравнение равновесия:

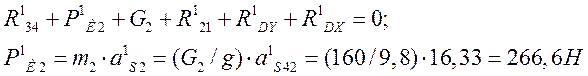
сила инерции центра масс звена 2;

В уравнении содержится 3 неизвестных, поэтому для построения найдем одно из них. Найдем величину силы , используя уравнение равновесия моментов сил приложенных к рассматриваемой группе:

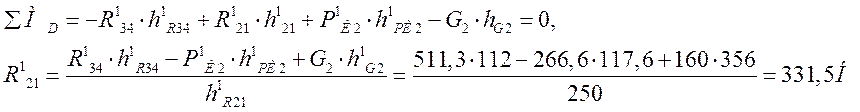
От произвольно выбранной точки  откладываем в масштабе силу  в виде отрезка  параллельно звену ВС, из точки  вертикально вниз откладываем в масштабе силу  в виде отрезка:

;

из точки параллельно ускорению  и в противоположном направлении откладываем отрезок ;

из точки  параллельно звену АВ откладываем в масштабе силу  в виде отрезка ;

через точку  проводим вертикальную линию, (направление силы ), через точку  горизонтально проводим линию направление действия силы  и при их пересечении получаем точку .

Отрезок  дает в масштабе  величину реакции ;

отрезок  дает в масштабе величину реакции .

          Уравновешивающий момент на ведущем звене определяется как момент силы  относительно оси вращения звена 1.

.