Собственные колебания системы с двумя степенями свободы

Министерство образования Российской Федерации

Санкт-Петербургский государственный горный институт им. Г.В. Плеханова

(технический университет)

РАСЧЁТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ № 2

	Детали машин

 

По дисциплине  __________________________________________________________

________________________________________________________________________

^{(наименование учебной дисциплины согласно учебному плану)}

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Собственные колебания системы с двумя степенями свободы

Тема:    

Вариант № 3

_____________________________________________________________________________

_____________________________________________________________________________

Автор: студент гр.   ММ-01   ____________________          /     Сергеева Н А      /

                                               ^{(подпись)                                          (Ф.И.О.)}

ОЦЕНКА:     _____________

Дата: ___________________

ПРОВЕРИЛ

Руководитель проекта    гл. преп-ль           ________________                      /Соколова Г В. /

                                                   ^{(должность)                               (подпись)                                                            (Ф.И.О.)}

Санкт-Петербург

2002

Найти движение системы, если в начальный момент точка А находится в положении статистического равновесия, груз смещен из своего положения равновесия вниз на расстояние 0,5 см. Все начальные скорости равны нулю. Построить график движения груза.

Система имеет две степени свободы. За обобщенные координаты примем вертикальные отклонения точки А и груза 1 от их положений статического равновесия. Эти координаты обозначим соответственно через h и h₁.

m1, кг	m2, кг	m3, кг	r2, см	R2, см	r, см	с, Н/м	l, см	h0, см	h0, см/с	с1, Н/м
6	27	6	6	9	8	675	30	0,4	1,8	50

            Кинетическая энергия системы, как и в РГР№1, вычисляется по формуле:

                                                              Т=Т₁+Т₂+Т₃;                                              (1)                                         

Однако теперь положение груза 1 определяется новой обобщенной координатой. Поэтому 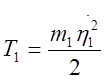. Кинетические энергии тел 2,3 вычисляются по старым формулам: 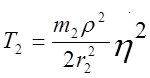  и .

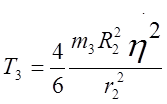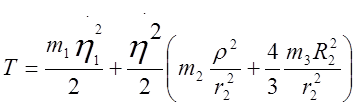            (2)

Выражение в скобках обозначим m.  Поэтому 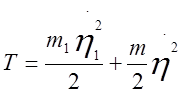, где m=66 кг

К потенциальной энергии, определяемой формулой: 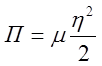, в РГР№1, добавится потенциальная энергия дополнительной пружины. При движении системы точка А (верхний конец) перемещается на величину h, нижний конец (груз 1) на величину h₁. Значит изменение длины пружины равно разности h₁-h, так что дополнительная потенциальная энергия может быть записана так:

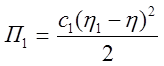
Потенциальная энергия всей системы будет иметь вид:

Исходная система с двумя степенями свободы сопоставлена со следующей эквивалентной двухмассовой системой. Уравнения  малых колебаний системы около положения устойчивого равновесия запишем в форме Лагранжа II рода.

h

c1

m

c

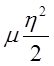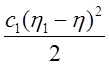П=+,            m=1800 Н/м

h1

m1

Приходим к следующей системе однородных линейных уравнений второго порядка с постоянными коэффициентами:

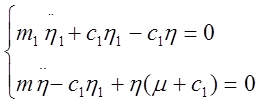
                         (3)                     

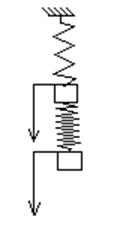
Система (3) описывает колебания двухмассовой системы, изображенной на рисунке 2.                                           
Решение этой системы ищем в виде:           h₁=Аsin(kt+a), h=Bsin(kt+a),                        (4)

где A, B, k, a - константы, подлежащие  определению. Подставим (4) в (3). После сокращения на общий множитель sin(kt+a) придем к однородной линейно-алгебраической системе:

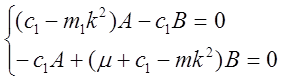                                                                                        (5)

Так как нас не интересует тривиальное решение, то потребуем, чтобы определитель системы (5) был равен нулю:

                                                                        (6)

Дальнейшее решение задачи проще выполнять с численными коэффициентами. Подставив в (6) заданные величины, получим:

99k⁴-3600k²+22500=0

Отсюда :       

Первому из уравнений (4) можно придать форму:

                                       h₁=А₁sin(5,31t+a₁)+A₂sin(2,83+a₂)                                   (7)

Так как определитель системы (5) равен нулю, значит коэффициенты А и В не являются независимыми. Из первого уравнения этой системы находим: В=(1-m₁k²/c₁)A

и, значит:            B₁=(1-6*28,3/50)A₁=-2,39A₁,         B₂=(1-6*8/50)A₂=0,04A₂

Поэтому второе уравнение (4) запишется так:

                                    h=-2,39А₁sin(5,31t+a₁)+0,04A₂sin(2,83t+a₂)                                   (8)

Постоянные А₁, А₂, a₁, a₂ найдем из начальных условий: t=0, h₁=0,5, h=0, 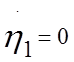, =0. Дифференцируем (7) и (8) по времени:

=5,31А₁cos(5,31t+a₁)+2,83A₂cos(2,83t+a₂)

                                  =-12,7A₁cos(5,31t+a₁)+0,11A₂cos(2,83t+a₂)                               (9)

Подстановка в (9) начальных условий дает:

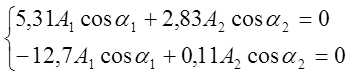
Квалифицируем эту систему как однородную и линейную относительно cosa₁ и cosa₂.  Определитель данной системы отличен от нуля, так как А₁¹0, А₂¹0. Значит, cosa₁=cosa₂=0, откуда a₁=a₂=p/2.

Подставим теперь начальные условия в (7) и (8). Это даст систему:

,

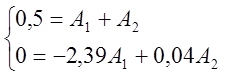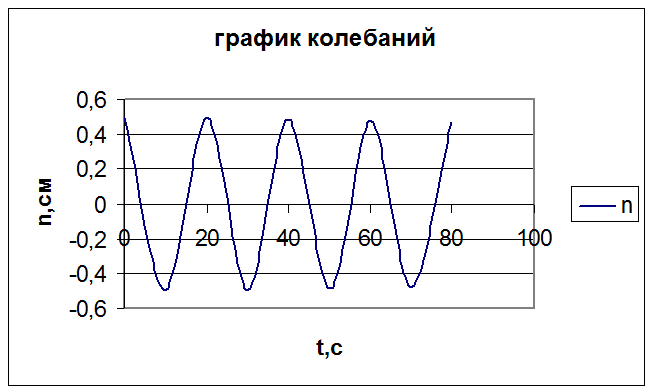
решение которой А₁=0,011 см, А₂=0,489 см. Уравнение движения груза 1 примет вид:

h₁=0,011cos5,31t + 0,489cos2,83t

Из (8) получаем:                        h=-0,026cos5,31t+0,02cos2,83t

График функции h₁=0,011cos5,31t + 0,489cos2,83t