Информатика и выч. техника \ Компьютерные технологии в науке и образовании

Применение метода сеток для решения задачи изгиба жестких плит

Страницы работы

17 страниц (Word-файл)
Скачать файл

Фрагмент текста работы

Министерство общего и профессионального образования

Российской Федерации

Санкт-Петербургский государственный горный институт им. Г.В. Плеханова

(технический университет)

КУРСОВАЯ  РАБОТА

По дисциплине         «Компьютерные технологии в науке и образовании»

________________________________________________________________________

(наименование учебной дисциплины согласно учебному плану)

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Тема: «Применение метода сеток для решения задачи изгиба жестких плит».

Автор: студент гр.   ВДм-00     ____________________           / Федотов А. В./

                                                               (подпись)                                       (Ф.И.О.)

ОЦЕНКА:     _____________

Дата: ___________________

ПРОВЕРИЛ

Руководитель проекта,      доцент               /Беляев В.В./

                                              (должность)                (подпись)                                            (Ф.И.О.)

Санкт-Петербург

2004 год

Оглавление

Введение. 4

1. Задание на курсовую работу. 5

2. Исходные данные. 5

3.Программа расчета прогиба плиты.. 6

4.Результаты расчёта. 7

Заключение. 16

Список использованной литературы.. 17


Аннотация

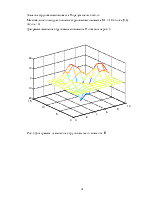
В данной курсовой работе осуществлено численное решение дифференциального уравнения в частных производных при помощи метода сеток для решения задачи изгиба жесткой плиты. Произведён расчёт прогиба плиты во всех внутренних и граничных точках, вычислены изгибающие моменты MX  и  MY  и скручивающий момент H. Построены диаграммы изменения прогиба плиты, изгибающих моментов MX и  MY и скручивающего момента Н.

The summary

In the given course work the numerical decision of the differential equation in individual grids, derivative through a method, for the decision of a task of a bend of a rigid plate is carried out. The account of a deflection of a plate in all internal and boundary points is made, the bending moments MX and MY and braiding moment H are calculated. The diagrams of change of a deflection of a plate bending moments MX and MY and braiding moment Н are constructed


Введение

В современной науке и технике математические методы исследования, моделирования и проектирования играют большую роль. Это обусловлено, прежде всего, быстрым развитием вычислительной техники, благодаря которой существенно расширяются возможности успешного применения математических методов при решении конкретных задач горного производства.

Целью выполнения курсовой работы является развитие и закрепление навыков программирования, овладение численными методами решения инженерных и математических задач, совершенствование работы на компьютере, а также умение применять компьютер при решении конкретных задач горного производства.


1. Задание на курсовую работу

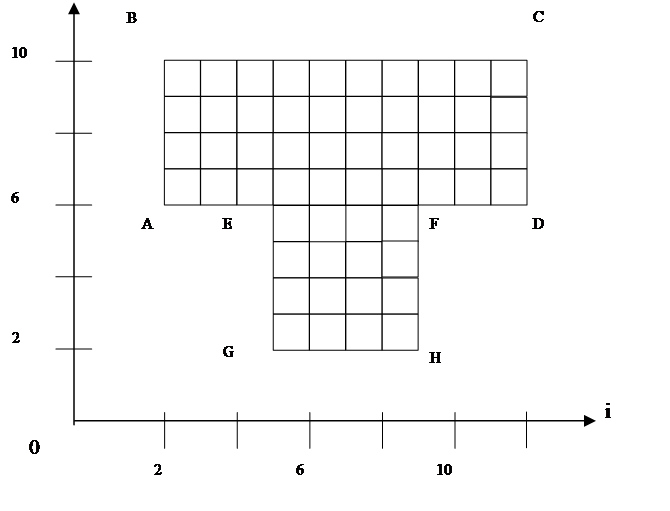
Найти прогиб плиты во всех внутренних и граничных точках, определить точку максимального прогиба. Вычислить изгибающие моменты MX и  MY . Вычислить скручивающий момент H. Определить точки, где изгибающие и скручивающие моменты принимают максимальные значения. Построить диаграммы изменения: прогиба плиты, изгибающих и скручивающих моментов.

2. Исходные данные

j
 
Плита имеет форму, показанную  на рисунке 1. Стороны AB, BC, CD, AE и FD жестко защемлены, а стороны  EG, GH и FH свободно опёрты на жесткий контур. Коэффициент Пуассона n=0,15. На плиту действует нагрузка q=3xy. Материал плиты – сталь с модулем упругости Е=2*105 . Точность вычислений e =0,0001.

 


Рис.1 Форма плиты

3.Программа расчета прогиба плиты

E=200000;

eps=0.0001;

nu=0.15;

d=E/12*(1-nu^2);

m=zeros(13,11); 

 n=m;

tt=2

konec=tt-0.0001

iter=0

while konec>0      защемлённый конец

      for j=6:1:10

         m(1,j)=m(3,j);

         m(11,j)=m(13,j);

      end

       for j=2:1:4

         m(4,j)=-m(6,j);

         m(10,j)=-m(8,j);

       end

         for i=2:1:12

         m(i,9)=m(i,11);

         End

         for i=2:1:3

             m(i,5)=m(i,7);

         end

         for i=11:1:12

             m(i,5)=m(i,7);

         end

         for i=5:1:9

             m(i,1)=-m(i,3)

         end

         m(4,5)=-0.5*(m(4,7)+m(6,5));

         m(10,5)=-0.5*(m(8,5)+m(10,7));

    for i=3:1:11

    for j=3:1:9

        x=i-2;

        y=j-2;

        q=3*x*y/d;

        if gran(i,j)==1

        m(i,j)=q/20+0.4*(m(i-1,j)+m(i+1,j)+m(i,j-1)+m(i,j+1))-0.1*(m(i-1,j-1)+m(i-1,j+1)+m(i+1,j-1)+m(i+1,j+1))-0.05*(m(i-2,j)+m(i+2,j)+m(i,j-2)+m(i,j+2));   

    end   

    end

   end

        tt=norm(m-n,2)

        konec=tt-0.001

        iter=iter+1

     n=m; 

end

b=n

for i=2:1:12;

    for j=2:1:10;

        n0=n(i,j);

        n1=n(i-1,j);

        n2=n(i,j-1);

        n3=n(i+1,j);

        n4=n(i,j+1);

        n5=n(i-1,j-1);

        n6=n(i+1,j-1);

        n7=n(i+1,j+1);

        n8=n(i-1,j+1);

        XM(i,j)=-d*(n1+n3+nu*(n2+n4)-2*n0*(1+nu));

        YM(i,j)=-d*(n2+n4+nu*(n1+n3)-2*n0*(1+nu));

        HXY(i,j)=-d*(1-nu)*(-n6+n7-n8+n5)/4;

    end

end

xmom=XM

ymom=YM

hmom=HXY

NMAX=max(max(n))

XMAX=max(max(xmom))

YMAX=max(max(ymom))

HMAX=max(max(hmom))

x=0:0.25:1;

y=0:0.25:1;

mesh(n)

mesh(XM)

mesh(YM)

mesh(HXY)

function rez=gran(i,j);

if and(and(i>=3,i<=11),and(j>=7,j<=9))

    rez=1;

elseif and(and(i>=6,i<=8),and(j>=3,j<=6))

    rez=1;

else

    rez=0;

end

return

Похожие материалы

Информация о работе

ВУЗ:
Национальный минерально-сырьевой университет «Горный» (НМСУ «Горный»)
Предмет:
Компьютерные технологии в науке и образовании
Тип:
Курсовые работы
Категория:
Информатика и выч. техника (Технические предметы)
Размер файла:
118 Kb
Скачали:
0
Скачать файл