Определение четности, нечетности и периодичности функции. Поиск критических точек и участков монотонности

Министерство образования Российской Федерации

Санкт-Петербургский  государственный горный  институт им. Г.В. Плеханова

(технический университет)

Кафедра Высшей математики

Расчетно-графическое задание №1

По дисциплине: Высшая математика

Вариант №9

Выполнил: ст.гр.ВД-03  _________      /Марченко А.В./

                                                                ^{(подпись)                      (Ф.И.О.)}                                                                                            

 Проверил: профессор  _________ /Господариков А.П./

                                                                                                      ^{(подпись)                     (Ф.И.О.)}                      

Оценка: _____________

Дата: _____________

Санкт-Петербург

2004

I.         y =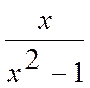

1. Найдем область определения функции:

D(y) = R, x 1

2. Определим четность, нечетность и периодичность функции:

y (-x)=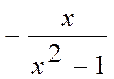 - функция нечетная  её график симметричен относительно начала координат.

3. Найдем критические точки и участки монотонности:

y’(x)

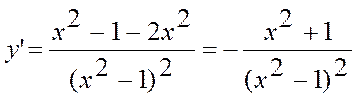
Функция убывает на всей области определения.

4. Находим вторую производную, точки перегиба и определим участки выпуклости и вогнутости.

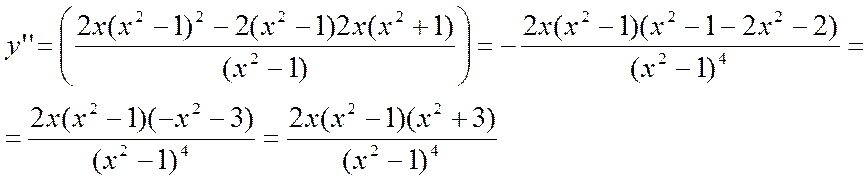
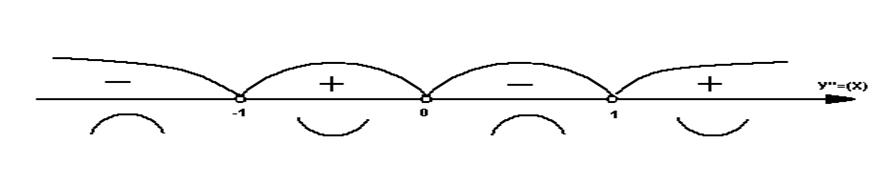
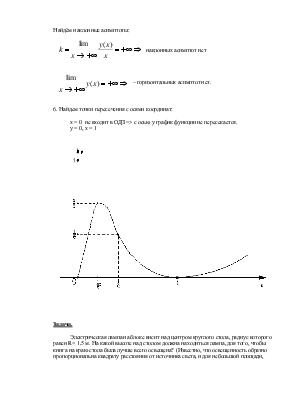
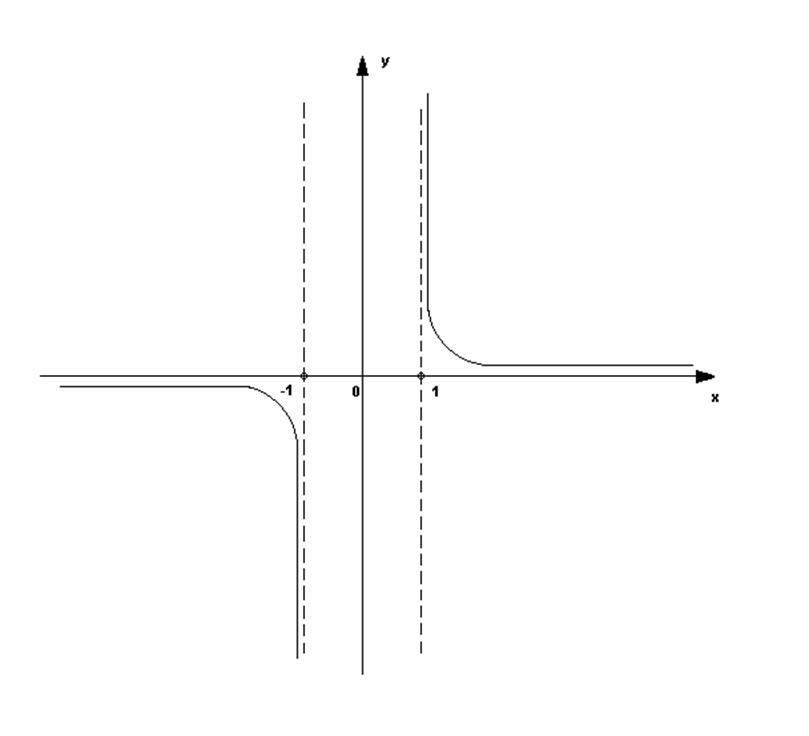
5. Определяем асимптоты:

Прямые х = -1 и х = 1 вертикальные асимптоты, так как,

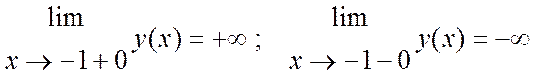
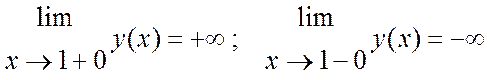
Найдём наклонные асимптоты:

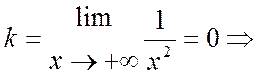
наклонных асимптот нет

Найдём горизонтальные асимптоты:

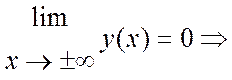
У = 0 – горизонтальная асимптота.

6. Найдем точки пересечения с осями координат:

х = 0, у = 0 – пересечение с осями координат

II. 

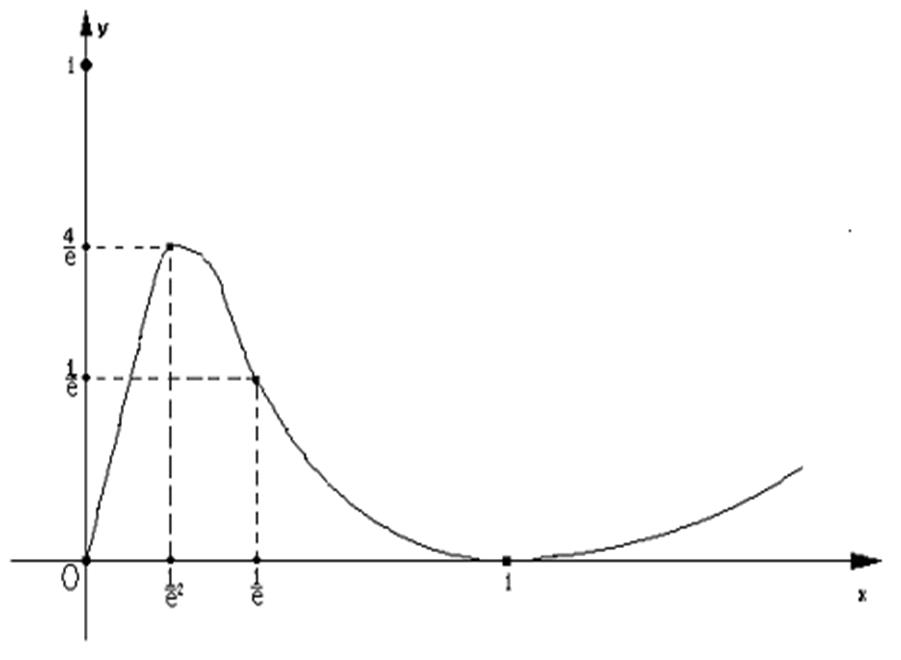
1. Найдем область определения функции:

D(y): х  >0

2. Определим четность, нечетность и периодичность функции:

у(-х) – при х>0 не существует функция не четная.

3. Найдем критические точки и участки монотонности:

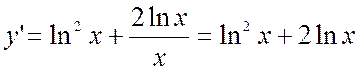
y’ = 0 т.е.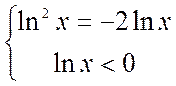

lnx > 0 = ln 1 => x [0;1]

lnx lnx = -2 lnx ; lnx (lnx -2) = 0

lnx = -2 => x =; lnx = 0 => x = 1

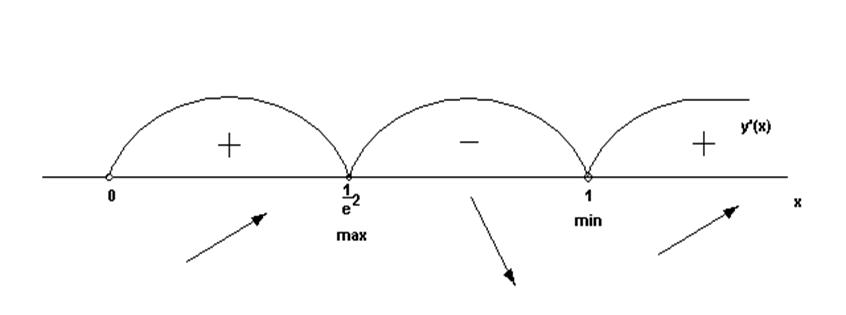
Функция возрастает на всей области определения.

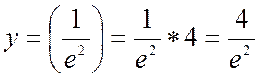
4. Находим вторую производную, точки перегиба и определим участки выпуклости и вогнутости.

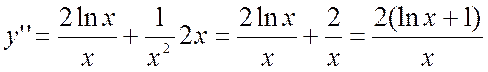
y’’= 0,  т.е.  ln x +1 = 0; lnx = -1; x =

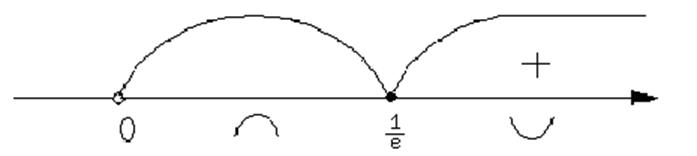
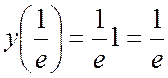
5. Определяем асимптоты:

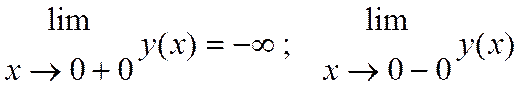
-  не существует => вертикальных асимптот нет.

-   

Найдём наклонные асимптоты:

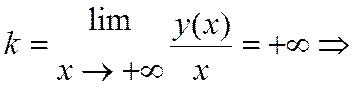
наклонных асимптот нет

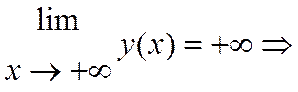
– горизонтальных асимптот нет.

6. Найдем точки пересечения с осями координат:

х = 0  не входит в ОДЗ => с осью у график функции не пересекается.

у = 0, х = 1

Задача.

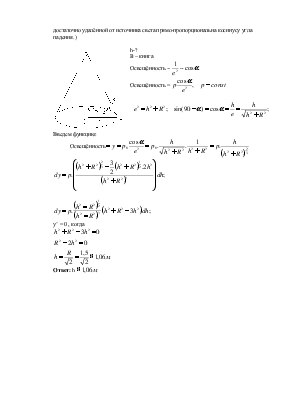
Электрическая лампа на блоке висит над центром круглого стола, радиус которого равен R= 1,5 м. На какой высоте над столом должна находиться лампа, для того, чтобы книга на краю стола была лучше всего освещена? (Известно, что освещенность обратно пропорциональна квадрату расстояния от источника света, и для небольшой площади, достаточно удалённой от источника света прямо-пропорциональна косинусу угла падения.)

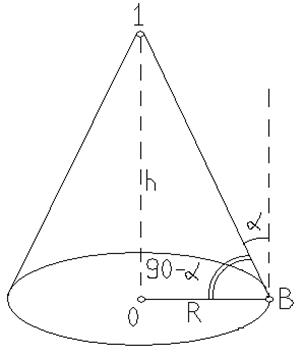h-?

B – книга

Освещённость ~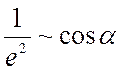

Освещённость =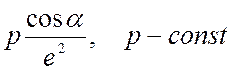

 
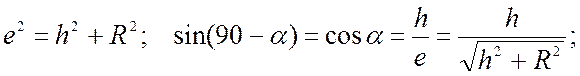
Введем функцию:     Освещённость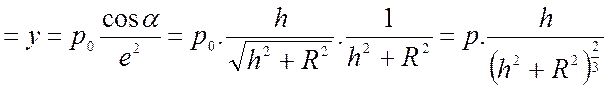

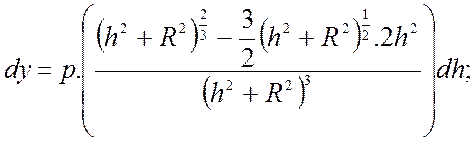
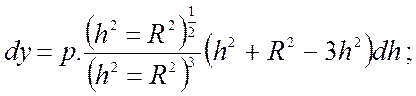
у’ = 0 , когда  

           

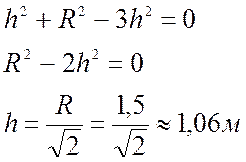
Ответ: h