Санкт Петербургский государственный горный институт
(технический университет)
Кафедра общей и технической физики
Лаборатория механики и молекулярной физики
Лабораторная работа 22
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ ГАЗОВ С ПОМОЩЬЮ ОСЦИЛЯТОРА ФЛАММЕРСФЕЛЬДА
 |
Экспериментальная установка
Санкт-Петербург 2008 г.
Работа 21 Определение показателя адиабаты газов при помощи осциллятора Фламерфельда.
Теоретическое введение.
Адиабатическим процессом называется процесс, происходящий без теплообмена с окружающей средой. Уравнение адиабатического процесса (уравнение Пуассона) имеет вид:
PVγ = const (1)
здесь:р – давление газа, V – объём газа, γ - показатель адиабаты.
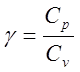
Ср – теплоёмкость газа при изобарном процессе (р = const), Сv – теплоёмкость газа при изохорном процессе (V = const).
Адиабатический процесс можно осуществить либо при хорошей теплоизоляции сосуда с газом, в котором происходит процесс, либо если производить процесс очень быстро, тогда теплообмен не будет успевать происходить. Поэтому все быстро протекающие процессы можно считать адиабатическими. На практике адиабатический процесс совершается в некоторых тепловых двигателях (например, в двигателях Дизеля). Распространение звука в газах (быстрое периодическое изменение давления в малых областях пространства) так же протекает адиабатически.
В данной работе определяется показатель адиабаты γ методом осциллятора Фламмерсфельда. Суть этого метода заключается в следующем. Представим себе узкую вертикальную стеклянную трубку (рис. 1) с открытым верхним концом. В трубке сбоку имеется небольшое отверстие (1), снизу в трубку подаётся газ или от компрессора, либо от баллона со сжатым газом. В трубку помещается небольшой легкий пластмассовый цилиндрик (2) (осциллятор Фламмерсфельда).
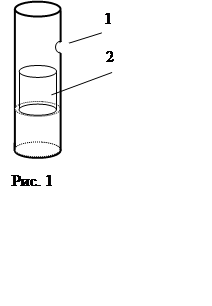
На уровне верхнего конца цилиндра давление сверху будет равно:
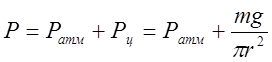 (2)
(2)
где Ратм – атмосферное давление, Рц – давление, обусловленное весом цилиндра, m – масса цилиндра, r – радиус цилиндра.
Снизу на цилиндр действует поток газа, создающего давление Р1. Если Р1= Р, то цилиндр находится в равновесии. Если увеличить поток газа, то Р1 станет больше Р, цилиндр начнёт подниматься. Когда нижний конец цилиндра окажется выше отверстия, то газ начнет выходить через отверстие, давление Р1 уменьшится, цилиндр начнет опускаться. Затем все будет повторяться снова. Таким образом, цилиндр будет совершать колебания (осциллировать) около отверстия. Так как. возникающие колебания происходят сравнительно быстро, то можно считать, что они происходят адиабатически, т.е. подчиняются уравнению (1).
Продифференцируем уравнение (1)
![]()
откуда
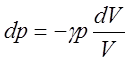 (3)
(3)
При изменении давления газа на dp его объём изменяется на dV и при этом цилиндр проходит малое расстояние х.
Тогда
![]() (4)
(4)
Подставляя (4) в (3) получим
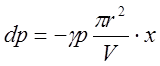 (5)
(5)
При изменении давления на dp на цилиндр снизу будет действовать сила
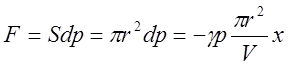 (6)
(6)
Эта сила будет
сообщать цилиндру ускорение 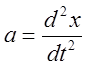
По второму закону Ньютона
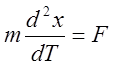 (7)
(7)
Подставляя (6) в (7) получим
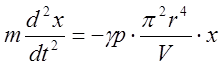
или
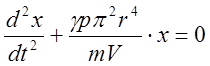 (8)
(8)
Введём обозначение
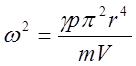 (9)
(9)
Тогда уравнение (8) перепишется так
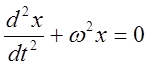 (10)
(10)
Это дифференциальное уравнение гармонических колебаний (гармонического осциллятора).
Круговая частота ω равна
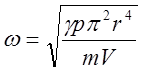 ;
;
Период колебаний
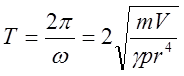
отсюда
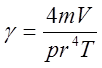 (11)
(11)
Таким образом, измеряя период колебания осциллятора можно вычислить γ.
Величина показателя адиабаты γ зависит не от рода газа, а от числа степеней свободы молекул газа, которое, в свою очередь, зависит от числа атомов в молекуле. У одноатомного газа всего 3 степени свободы (поступательных), у двухатомного – 5 степеней свободы (3 поступательных и 2 вращательных), у трехатомного газа 6 степеней свободы (3 поступательных и 3 вращательных).
Через степени свободы показатель адиабаты γ выразится так:
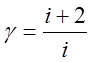
где i – число степеней свободы молекулы
для одноатомных газов i = 3. γ =1,67;
для двухатомных газов i = 5. γ =1,40;
для трехатомных газов i = 6. γ =1,33.
 Общий вид
экспериментальной установки показан на рис. 2.
Общий вид
экспериментальной установки показан на рис. 2.
От компрессора (1) воздух накачивается в балластную стеклянную банку (2). Снизу этой банки имеется клапан (3), с помощью которого можно точно регулировать поток газа (и давление), подаваемого в измерительную колбу (4). Сверху в эту колбу на шлифе вставлена трубка (5), в которую помещён лёгкий пластмассовый цилиндр (6) (осциллятор). Сбоку в трубке имеется небольшое отверстие, расположенное симметрично между двумя синими полосками на трубке. Регулируя клапаном подачу воздуха в измерительную колбу нужно добиться того, чтобы осциллятор совершал колебания между этими двумя полосками. Период этих колебаний измеряется с помощью устройства, называемого световым барьером (7).
В этом устройстве имеется источник света и приёмник света. Стеклянная трубка с осциллятором располагается на пути светового луча. При колебаниях осциллятора он периодически перекрывает луч света и в датчике светового барьера возникает периодический электрический сигнал. С помощью цифрового дисплея имеющегося на этом устройстве можно измерить период колебаний осциллятора.
Порядок выполнения работы.
1. Убедитесь, что экспериментальная установка собрана согласно рис. 2. Все пробки в стеклянных сосудах вставлены достаточно плотно.
2. Отрегулируйте взаимное расположение светового барьера и стеклянной трубки с осциллятором. Луч света должен проходить по диаметру трубки на высоте вблизи верхней или нижней полоски на трубке.
3. Включите питание светового барьера, выберите режим COUNT (счетчик колебаний).
4. Включите компрессор и с помощью клапана (3) установите такой поток воздуха, чтобы осциллятор колебался между двумя полосками на трубке.
Внимание. Во избежании вылета осциллятора из трубки при большом потоке газа слегка прикрывайте рукой верхней конец трубки.
5. На световом барьере нажмите кнопку Reset (сброс) и одновременно включите секундомер.
6. Когда счетчик светового барьера покажет цифру 50 (50 полных колебаний) остановите секундомер.
7. Разделив время, измеренное по секундомеру, на 50, получим период колебаний осциллятора.
8. По формуле (11) рассчитать показатель адиабаты.
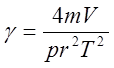
Значения величин входящих в эту формулу следующее:
m = 4,6.10-3 кг – масса осциллятора,
V = 1.14.10-3 м3 – объём измерительной колбы,
Т – измеренный период колебаний,
Р = 105 Па (ввиду малого веса осциллятора давление можно считать равным атмосферному),
r = 5,95.10-3 м – радиус осциллятора.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.