|
ΔH |
Vt |
Температура |
|||||||||||
|
воздуха |
рекуператора |
середины стенки трубы |
|||||||||||
|
на входе |
на выходе |
в начале |
в середине |
в конце |
|||||||||
|
42 |
0,00356 |
0 |
0 |
14 |
194 |
35 |
440 |
33 |
418 |
28 |
361 |
18 |
243 |
|
38 |
0,00339 |
1 |
16 |
14 |
194 |
21 |
279 |
20 |
267 |
28 |
361 |
30 |
384 |
|
31,5 |
0,00309 |
1 |
16 |
11 |
156 |
1 |
255 |
17 |
231 |
27 |
349 |
25 |
326 |
|
31 |
0,00306 |
1 |
16 |
11 |
156 |
16 |
219 |
14 |
194 |
26 |
338 |
22 |
291 |
|
28 |
0,00291 |
1 |
16 |
9 |
130 |
16 |
219 |
12 |
169 |
24 |
314 |
19 |
255 |
|
25 |
0,00275 |
1 |
16 |
9 |
130 |
15 |
206 |
11 |
116 |
23 |
303 |
16 |
219 |
|
18 |
0,00233 |
1 |
16 |
9 |
130 |
14 |
194 |
11 |
116 |
10 |
143 |
17 |
231 |
|
14,5 |
0,00209 |
1 |
16 |
9 |
130 |
14 |
194 |
11 |
116 |
22 |
291 |
16 |
219 |
|
5,5 |
0,00129 |
0 |
0 |
9 |
130 |
14 |
194 |
12 |
169 |
21 |
249 |
16 |
219 |
|
1 |
0,00055 |
0 |
0 |
9 |
130 |
14 |
194 |
12 |
169 |
20 |
267 |
16 |
219 |
Температурная поправка на температуру холодного спая равна 23º С.
Для определения вида критериального уравнения составим вспомогательную таблицу расчетов:
|
H |
Vo |
tст сред |
tвозд сред |
|
42 |
0,00329 |
388,50 |
120 |
|
38 |
0,00297 |
345,75 |
128 |
|
31,5 |
0,00270 |
313,25 |
109 |
|
31 |
0,00268 |
283,50 |
109 |
|
28 |
0,00255 |
262,25 |
96 |
|
25 |
0,00241 |
234,00 |
96 |
|
18 |
0,00204 |
194,00 |
96 |
|
14,5 |
0,00183 |
228,00 |
96 |
|
5,5 |
0,00119 |
230,75 |
88 |
|
1 |
0,00051 |
235,25 |
88 |
|
СРЕДНЕЕ |
|||
|
23,45 |
0,00222 |
271,53 |
102,6 |
Количество
тепла, переданного за единицу времени равно ![]() .
.
Удельная теплоемкость воздуха при средней температуре воздуха 102,6º С равно 1,3051 кДж/(м3·К). Значит
![]()
Коэффициент
теплоотдачи определим по формуле 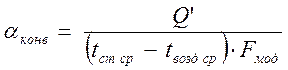 .
.
Таким образом, 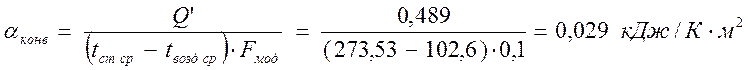
Коэффициент теплопроводности λ для средней температуры воздуха 102,6º С равен 3,22·10-2 Вт/м·К .
Линейный размер модели ![]() .
.
Значение критерия Нуссельта 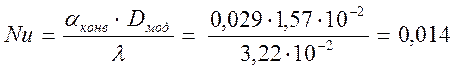
Расход воздуха, проходящий через модель при средней температуре воздуха равен:
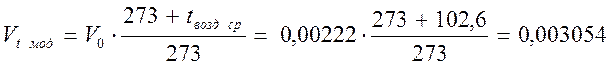
Значение скорости определяем по формуле:
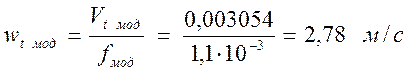
Вычислим критерий Рейнольдса. При вычислении этого критерия за определяющий размер принимаем гидравлический диаметр модели рекуператора. Кинематический коэффициент вязкости при температуре 102,6º С равен 23,13·10-6.
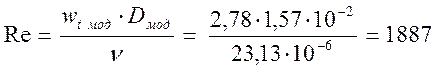
Для различных режимов работы рассчитаем критерии Нуссельта и Рейнольдса и завнесем их в таблицу:
|
H |
tвозд сред |
αконв |
Nu |
w |
Re |
|
42 |
120 |
0,0329 |
58,5093 |
4,30 |
2920 |
|
38 |
128 |
0,0297 |
62,4099 |
3,96 |
2689 |
|
31,5 |
109 |
0,0270 |
53,1460 |
3,44 |
2332 |
|
31 |
109 |
0,0268 |
53,1460 |
3,41 |
2314 |
|
28 |
96 |
0,0255 |
46,8075 |
3,13 |
2124 |
|
25 |
96 |
0,0241 |
46,8075 |
2,96 |
2007 |
|
18 |
96 |
0,0204 |
46,8075 |
2,51 |
1703 |
|
14,5 |
96 |
0,0183 |
46,8075 |
2,25 |
1528 |
|
5,5 |
88 |
0,0119 |
42,9068 |
1,43 |
971 |
|
1 |
88 |
0,0051 |
42,9068 |
0,61 |
414 |
Обычно критериальные уравнения имеют
вид степенной функции ![]()
где c и n – коэффициенты, найденные экспериментально.
Для нахождения коэффициентов c и n логарифмируем уравнение и получим:
![]()
|
ln Nu |
ln Re |
|
4,07 |
7,98 |
|
4,13 |
7,90 |
|
3,97 |
7,75 |
|
3,97 |
7,75 |
|
3,85 |
7,66 |
|
3,85 |
7,60 |
|
3,85 |
7,44 |
|
3,85 |
7,33 |
|
3,76 |
6,88 |
|
3,76 |
6,03 |
Построим зависимость Nu = f ( Re ).
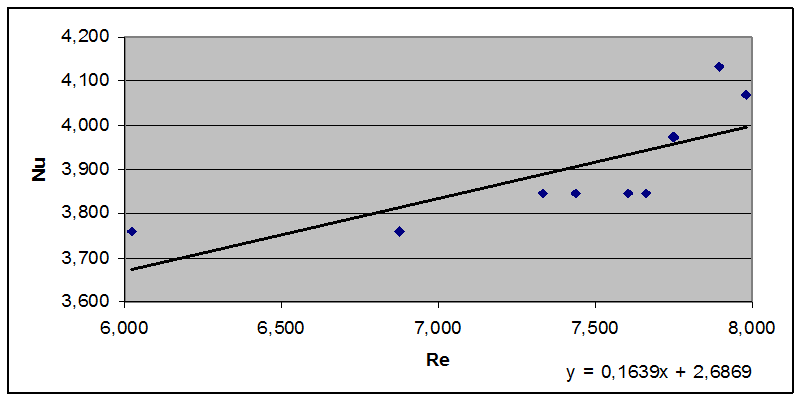
Таким образом, ln c = 2,6869 ( с = 14,686 ) и n = 0,1639.
Значит, критериальное уравнение примет вид:
![]()
Полученное критериальное уравнение описывает процесс конвективного теплообмена в модели рекуператора и в подобном ему промышленном рекуператоре, что позволяет использовать это уравнение для расчета промышленного рекуператора.
1) Расход проходящего через рекуператор воздуха составляет 200 м3/мин.
2) Средняя температура нагретого воздуха 300º С.
3) Средняя температура поверхности рабочих элементов рекуператора 800º С.
4) Гидравлический диаметр 3,86·10-2 м.
Определим критерий Рейнольдса при условии, что w = 10 м/с и ν = 102,34·10-6.
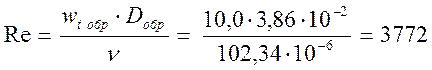
Тогда критерий Нуссельта будет равен
![]()
Коэффициент теплоотдачи равен:
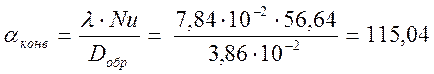
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.