Определение g-фактора электрона с помощью электронного парамагнитного резонатора, страница 2

μ_JB = -g_∙μ_B∙m_J                                                            (2)

где μ_B — магнетон Бора, m_J = -J, -(J-1), …, J-1, J - магнитное квантовое число, а 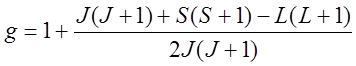 - так называемый g-фактор Ланде электрона; J, L и S - квантовые числа. Для магнитного квантового числа m_J имеется правило отбора, согласно которому возможны только переходы, при которых m_J либо остается неизменным, либо меняется на единицу Δm_J = 0, ±1.

В простейшем случае свободного электрона L=0, J=S=1/2, m_J = ±1/2, g =2,00 и энергия E свободного электрона может принимать два значения:

E₁ = -g∙μ_B∙B/2∙                       и                      E₂ = g∙μ_B∙B/2                         (3)

Переходы между магнитными подуровнями возможны, когда квант электромагнитной энергии ћω равен разности энергий между ними:

ћω = E₂-E₁ = gμ_BB                                                         (4)

Переход электрона с одного подуровня на другой происходит с одновременным изменением направления спина:

Δm_S = ±1.                                                         (5)

Для частиц, содержащих несколько электронов, S может принимать любое кратное 1/2 значение (рис. 1б, 1в), а величина g-фактора определяется суммарным значением спинового и орбитального моментов количества движения электрона и может в несколько раз отличаться от значения для свободного электрона.

На практике имеют дело с макроскопическими образцами, содержащими огромное количество парамагнитных атомов или молекул. В таких системах действуют статистические законы, в соответствии с которыми большая часть парамагнитных частиц находится в состоянии с минимальной энергией. В соответствии с распределением Больцмана

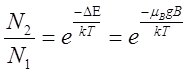,                                                   (6)

населённость нижнего уровня N₁ больше, чем верхнего N₂. Это означает, что большинство парамагнитных атомов или молекул ориентируют свои магнитные моменты по направлению магнитного поля. Несколько меньшее число атомов располагается так, что их магнитные моменты составляют с внешним полем некоторый угол, и меньше всего атомов имеет максимальную энергию, соответствующую направлению магнитных моментов атомов против поля.

Такое распределение частиц по уровням в определенном смысле обладает свойствами устойчивого равновесия, известного в обычной механике: если каким-либо способом изменить это распределение, то через некоторое время оно снова вернется в равновесное состояние. При равновесном распределении, когда большинство частиц обладает минимальной энергией, поглощение электромагнитной энергии всегда должно преобладать над ее излучением, что и наблюдается в ЭПР. Если каким-либо образом создать инверсию населённостей , то под действием электромагнитного поля система будет излучать энергию.

Взаимодействие электронов с электромагнитным внутрикристаллическим полем приводит для S≥1 к расщеплению уровней энергии с разными значениями |M_S| и без магнитного поля (при B=0). В результате этого в спектре ЭПР появляется несколько линий поглощения (тонкая структура; рис. 3а).

Взаимодействие электронов с магнитным моментом ядра парамагнитного атома приводит к появлению в спектре ЭПРсверхтонкой структуры. Рассмотрим атом, в котором неспаренный электрон взаимодействует с одним протоном (спин протона I=1/2). Во внешнем магнитном поле B, так же как и для электрона, будут реализовываться две ориентации магнитного момента протона: по полю M_I = 1/2 и против поля M_I=-1/2. Магнитный момент протона создает в месте нахождения электрона дополнительное магнитное поле ΔB_I. Поэтому при напряженности внешнего магнитного поля B₀ неспаренные электроны тех атомов, у которых M_I = 1/2, окажутся в суммарном поле B = B₀+ΔB_I. В атомах, у которых M_I = -1/2, величина суммарного поля равна B = B₀-ΔB_I. В магнитном поле энергии ядер в состояниях с M_I = 1/2  и M_I = -1/2 практически не различаются, поэтому число ядер в этих состояниях практически одинаково. Отсюда и число электронов, находящихся в дополнительных полях +ΔB_I и -ΔB_I также одинаково. Таким образом, каждый энергетический уровень неспаренного электрона расщепится на два равнозаселенных уровня (рис. 3б). Правило отбора при электронных переходах ΔM_I=0. Это значит, что за время электронного перехода не происходит изменения ориентации ядерного спина.