Механика \ Механика

Момент инерции различных тел. Теорема Штейнера, страница 2

j

F

l

M

p/2

p

3p/2

2p

Проделайте эти измерения для углов j, равных 180о, 270о, 360о. Полученные данные занесите в таблицу.

По полученным данным постройте график зависимости М от j.

Тангенс угла наклона прямой будет численно равен модулю кручения D пружины.

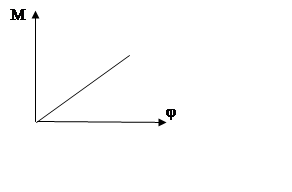Далее следует измерить период колебаний системы с исследуемым телом. Для измерения периода используется устройство называемое световым барьером. Оно состоит из источника света и приемника света. На ось пружины насажена непрозрачная полоска, размещаемая между источником и приемником света. При колебаниях эта пластинка периодически перекрывает луч света. Световой барьер может работать в нескольких режимах, которые устанавливаются с помощью переключателя. Он может измерять или число колебаний, или полпериода, или целый период колебаний. Удобнее использовать режим измерения периода колебаний. Для этого переключатель устанавливают в положение, при котором на индикаторе высвечиваются четыре точки.

Процедура измерения периода следующая.

1.  Насадите на ось пружины исследуемое тело.

2.  Расположите всю систему так, чтобы непрозрачная полоска перекрывала луч света от источника.

3.  Закрутите пружину на 180о и отпустите.

4.  После того как на индикаторе появится значение периода, запишите это значение и нажмите кнопку на световом барьере (обнулите показания индикатора).

5.  Повторите измерения периода 5 – 10 раз.

6.  Найдите среднее значение периода.

В данной работе можно выполнять несколько заданий.

А. Определение моментов инерции различных тел относительно оси, проходящей через центр симметрии.

1.  Выберите определенное тело и насадите его на ось пружины.

2.  Измерьте период колебаний системы описанным выше способом.

3.  По измеренным D и  T по формуле (9) вычислите экспериментальное значение  момента инерции.

4.  Измерьте радиус тела и определите его массу (взвесив тело).

5.  По одной из формул (1 – 5) вычислите теоретическое значение момента инерции для данного тела.

Проведите измерения для различных тел (по указанию преподавателя). Можно измерять моменты инерции стержня без грузов, стержня с грузами, диска, шара, сплошного цилиндра, полого цилиндра.

В. Изучение зависимости момента инерции от расстояния масс от оси вращения.

1.  Насадите на ось пружины стержень с симметрично расположенными грузами.

2.  Расположите грузы на ближайшем расстоянии от оси вращения. Измерьте расстояние r от оси вращения до центров  грузов.

3.  Измерьте период колебаний системы.

4.  Последовательно смещайте грузы на 2 см и измеряйте период.

5.  По формуле (9) рассчитайте момент инерции для каждого положения грузов.

6.  Составьте таблицу.

r, (м)

r2, (м2)

T, (с)

J, (кг.*м2)

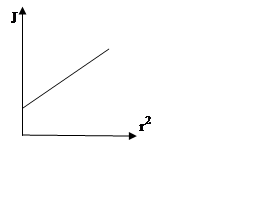
7.  По данным таблицы постройте график зависимости J=f(r2).

8.  Теоретическую формулу для момента инерции стержня с грузами можно записать в виде

Здесь Jст-момент инерции стержня, m –масса одного груза.

В параметрах  J=f(r2) это уравнение прямой, не проходящей через начало координат. Отрезок, осекаемый экспериментальным графиком на оси ординат равен моменту инерции стержня Jст. Сравните это значение с теоретическим значением Jст .

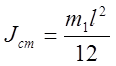
Здесь  m1 –масса стержня, l – длина стержня.

С. Проверка теоремы Штейнера.

1.  Насадите на ось пружины стержень без грузов. Ось пружины должна совпадать с центром стержня.

2.  Измерьте период колебаний и вычислите момент инерции Jo формуле (9).

3.  Сместите стержень на некоторое расстояние d от центра.

4.  Измерьте период колебаний и вычислите момент инерции J .

5.  Согласно теореме Штейнера

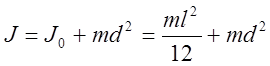
где l –длина стержня, m – масса стержня.

6.  Измерьте массу стержня, его длину и расстояние d.

7.  Вычислите теоретическое значение J по этой формуле и сраните его с экспериментальным значением J.

Скачать файл