Масштабный коэффициент:
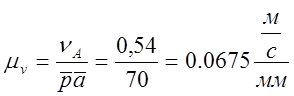 , где
, где ![]() -
чертёжное изображение скорости точки А, равное 50 мм;
-
чертёжное изображение скорости точки А, равное 50 мм; ![]() -
линейная скорость точки А,
-
линейная скорость точки А, 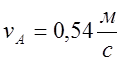 .
.
По теореме о сложении скоростей полная скорость точки В в относительном движении точки А:
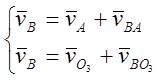 -
- ![]() ,
, ![]() скорости
относительного движения
скорости
относительного движения
Решаем векторное уравнение графически:
Из полюса Р проводим вектор VA перпендикулярно О1А. Из конца VA выходит начало VBA перпендикулярно АВ. Из полюса Р проводим прямую, параллельную линии действия точки В. Пересечение этих прямых есть решение уравнения. А точки С,D , будут выходить из с конца вектора VA и будут направлены по линии действия VBA.
На основании построенных планов скоростей определим полные скорости всех характерных подвижных точек звеньев механизма:
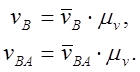
Скорости vc , vD находятся аналогично.
Для нахождения полных скоростей центров масс звеньев воспользуемся свойством подобия планов скоростей.
![]()
где
![]() - чертёжное изображение скорости точки S3 .
- чертёжное изображение скорости точки S3 .
Результаты вычислений указанных величин приведены ниже в таблице 4.
Таблица 4
|
Положение механизма |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
70 |
70 |
70 |
70 |
70 |
70 |
|
|
0,54 |
0,54 |
0,54 |
0,54 |
0,54 |
0,54 |
|
|
62 |
69 |
46 |
9 |
24 |
63 |
|
|
1,10 |
3,5 |
0,11 |
1,50 |
1,96 |
1,92 |
|
|
22 |
7 |
34 |
75 |
67 |
17 |
|
|
0,97 |
2,37 |
1,92 |
0,56 |
0,34 |
0,08 |
|
|
7 |
19 |
17 |
4 |
2 |
14 |
|
|
0,26 |
0,71 |
0,64 |
0,15 |
0,08 |
0,53 |
|
|
76 |
71 |
46 |
97 |
94 |
75 |
|
|
0,71 |
1,92 |
1,73 |
0,41 |
0,26 |
1,43 |
|
|
14,5 |
46,5 |
1,5 |
20 |
26 |
25,5 |
|
|
0,55 |
1,75 |
0,06 |
0,75 |
0,98 |
0,96 |
|
|
2,26 |
5,51 |
4,47 |
1,30 |
0,79 |
0,19 |
Пример расчета для 1 положения механизма:
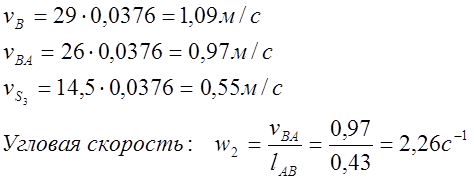
3.Построение планов ускорений механизма.
План ускорений механизма – совокупность планов ускорений всех звеньев механизма.
План ускорений звена – пучок лучей, выходящий из 1 полюса, на который в едином масштабе изображаются абсолютные ускорения точек звена механизма.
Определим нормальное ускорение
точки А: 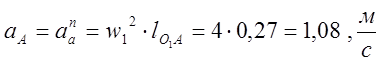
Абсолютное ускорение точки А: ![]()
Масштабный коэффициент: 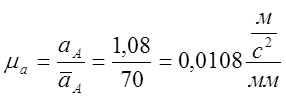
По теореме о сложении ускорений в сложном движении абсолютное ускорение точки, участвующей в сложном движении, равно геометрической сумме ускорений движений составляющих:
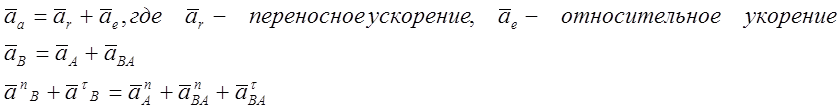
Решаем векторное уравнение графически:
Из полюса ![]() проводим
вектор
проводим
вектор ![]() параллельно О1А. Из конца
параллельно О1А. Из конца![]() , параллельно АВ – вектор
, параллельно АВ – вектор ![]() . К нему проведём перпендикуляр. Из полюса
. К нему проведём перпендикуляр. Из полюса ![]() , проводим вектор
, проводим вектор ![]() .
Его длину необходимо рассчитать по формуле:
.
Его длину необходимо рассчитать по формуле:
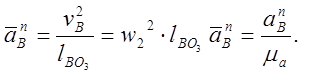 аналогично рассчитаем
аналогично рассчитаем ![]() .
.
Из конца проводим ![]() перпендикуляр, линия действия ВО3. Получим
перпендикуляр, линия действия ВО3. Получим
![]() соответственно. Ускорения точек C и D – будут лежать на прямой ВА.
Найдя их положения с помощью соответствующих пропорции, из полюса проведём
вектора
соответственно. Ускорения точек C и D – будут лежать на прямой ВА.
Найдя их положения с помощью соответствующих пропорции, из полюса проведём
вектора ![]() соответственно.
соответственно.
Рассчитаем значения ускорений по формулам:
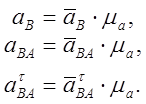
Аналогично рассчитаем ускорения для других оставшихся точек и занесём полученные результаты в таблицу:
Таблица 5
|
Положение механизма |
3 |
5 |
|
|
1,08 |
1,08 |
|
|
70 |
70 |
|
|
2,2 |
0,74 |
|
|
20 |
31 |
|
|
48 |
84 |
|
|
3,03 |
5,65 |
|
|
47 |
10 |
|
|
24,9 |
19,2 |
|
|
60 |
56 |
|
|
21,4 |
19,9 |
|
|
85 |
75 |
|
|
30,3 |
26,7 |
|
|
57,9 |
44,7 |
Пример расчета для 3 положения механизма:
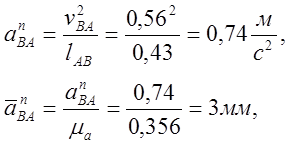
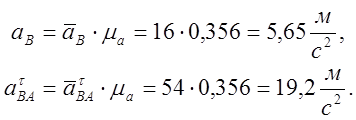
Угловое ускорение: ![]()
![]()
![]()
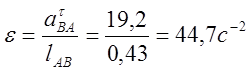
-
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.