
Санкт-Петербургский государственный горный институт им. Г.В. Плеханова
(технический университет)
Расчетно-графическое задание
|
![]() По
дисциплине
________________________________________________________________________
По
дисциплине
________________________________________________________________________
(наименование учебной дисциплины согласно учебному плану)
|
Тема:
|
|||
Автор: студент гр. АПМ-02 ____________________ / /
(подпись) (Ф.И.О.)
|
Руководитель работы доцент ________________ //
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
2004
Исходные данные:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; масштаб
; масштаб ![]() (
(![]() ).
).
Задача №1.
Аппроксимация кривой намагничивания методом гиперболического синуса.
Решение:
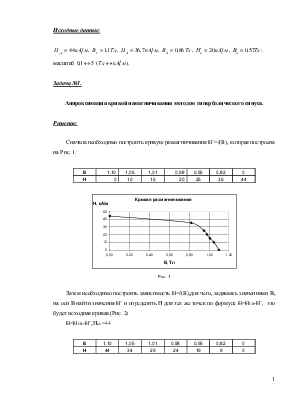
Сначала необходимо построить кривую размагничивания H’=f(B), которая построена на Рис. 1.
|
В |
1,10 |
1,05 |
1,01 |
0,98 |
0,95 |
0,82 |
0 |
|
Н |
0 |
10 |
15 |
20 |
25 |
35 |
44 |
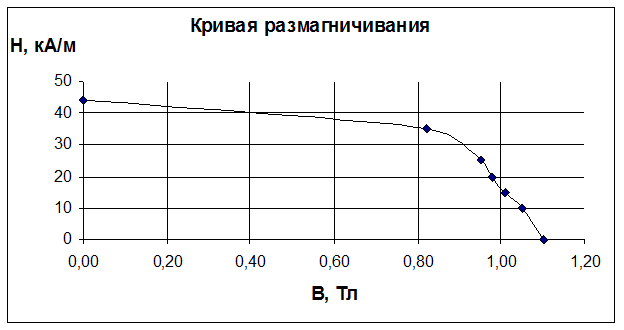
Рис. 1
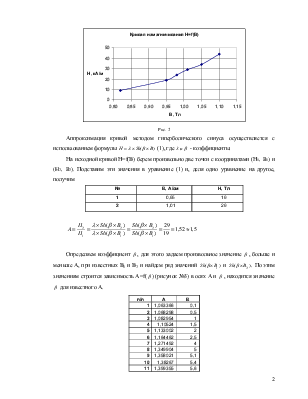
Затем необходимо построить зависимость H=f(B),для чего, задаваясь значениями В, на оси В найти значения H’ и определить Н для тех же точек по формуле H=HCB-H’, это будет исходная кривая.(Рис. 2)
H=HCB-H’, Нсв =44
|
B |
1,10 |
1,05 |
1,01 |
0,98 |
0,95 |
0,82 |
0 |
|
H |
44 |
34 |
29 |
24 |
19 |
9 |
0 |
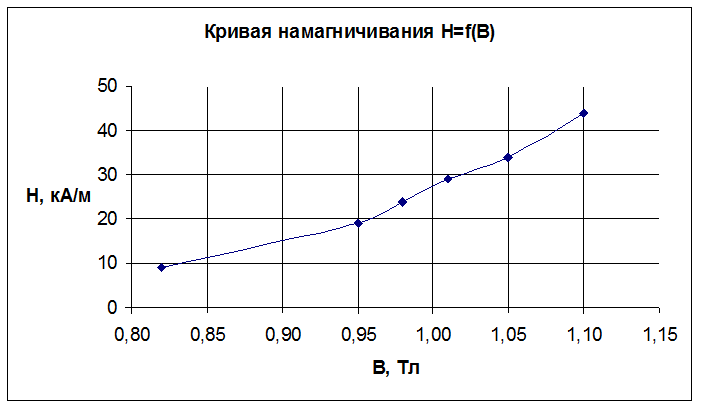
Рис. 2
Аппроксимация кривой методом гиперболического синуса осуществляется с
использованием формулы ![]() (1), где
(1), где ![]() - коэффициенты.
- коэффициенты.
На исходной кривой Н=f(B) берем произвольно две точки с координатами (H1, B1) и (H2, B2). Подставим эти значения в уравнение (1) и, деля одно уравнение на другое, получим
|
№ |
В, А/см |
Н, Тл |
|
1 |
0,95 |
19 |
|
2 |
1,01 |
29 |
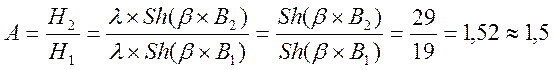
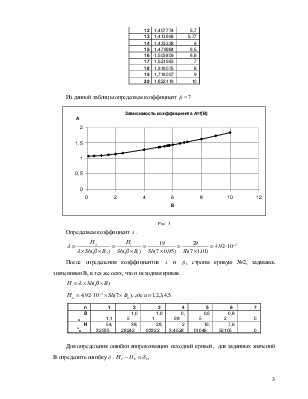
Определяем коэффициент ![]() , для этого задаем
произвольное значение
, для этого задаем
произвольное значение ![]() , больше и меньше А, при
известных B1 и B2 и найдем ряд значений
, больше и меньше А, при
известных B1 и B2 и найдем ряд значений ![]() и
и ![]() . По
этим значениям строится зависимость А=f(
. По
этим значениям строится зависимость А=f(![]() )
(рисунок №3) в осях А и
)
(рисунок №3) в осях А и ![]() , находится значение
, находится значение ![]() для известного А.
для известного А.
|
n/n |
A |
B |
|
1 |
1,063366 |
0,1 |
|
2 |
1,068298 |
0,5 |
|
3 |
1,082954 |
1 |
|
4 |
1,10524 |
1,5 |
|
5 |
1,133002 |
2 |
|
6 |
1,164462 |
2,5 |
|
7 |
1,271492 |
4 |
|
8 |
1,349904 |
5 |
|
9 |
1,358021 |
5,1 |
|
10 |
1,38267 |
5,4 |
|
11 |
1,399355 |
5,6 |
|
12 |
1,407774 |
5,7 |
|
13 |
1,413698 |
5,77 |
|
14 |
1,433338 |
6 |
|
15 |
1,476984 |
6,5 |
|
16 |
1,503809 |
6,8 |
|
17 |
1,521963 |
7 |
|
18 |
1,616075 |
8 |
|
19 |
1,716007 |
9 |
|
20 |
1,822119 |
10 |
Из данной таблицы определяем коэффициент ![]() = 7
= 7
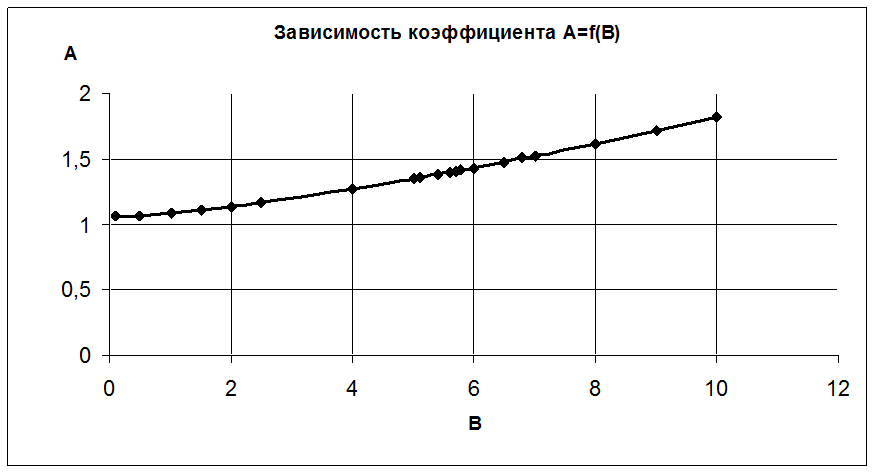
Рис. 3
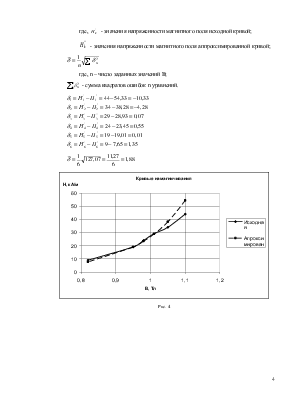
Определяем коэффициент ![]() .
.
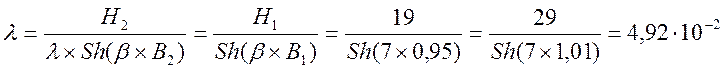
После определения коэффициентов ![]() и
и ![]() , строим кривую №2, задаваясь значениями В,
в тех же осях, что и исходная кривая.
, строим кривую №2, задаваясь значениями В,
в тех же осях, что и исходная кривая.
![]()
![]()
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Bn |
1,1 |
1,05 |
1,01 |
0,98 |
0,95 |
0,82 |
0 |
|
H”n |
54,32535 |
38,28242 |
28,93322 |
23,4528 |
19,01046 |
7,652105 |
0 |
Для определения ошибки аппроксимации исходной кривой, для заданных
значений В определить ошибку ![]() .
. ![]()
где, ![]() - значения напряженности магнитного поля исходной
кривой;
- значения напряженности магнитного поля исходной
кривой;
![]() - значения напряженности магнитного поля аппроксимированной
кривой;
- значения напряженности магнитного поля аппроксимированной
кривой;
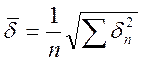
где, n – число заданных значений В;
![]() - сумма квадратов ошибок n уравнений.
- сумма квадратов ошибок n уравнений.
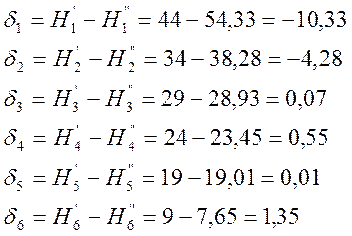
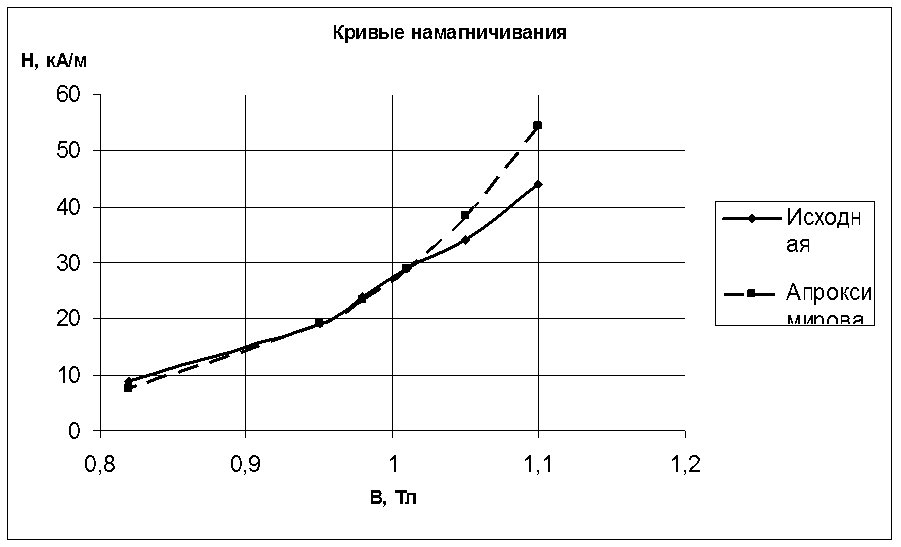
Рис. 4
Задача №2:
Аппроксимация кривой намагничивания методом степенного ряда (методом наименьших квадратов).
Исходные
данные берем из задачи 1. Кривая намагничивания стоится с использованием
формулы ![]() , при тех же значениях В, что и в первой
задаче. Для каждого значения В определяем ошибку
, при тех же значениях В, что и в первой
задаче. Для каждого значения В определяем ошибку ![]() :
:
|
B |
1,10 |
1,05 |
1,01 |
0,98 |
0,95 |
0,82 |
0 |
|
H |
44 |
34 |
29 |
24 |
19 |
9 |
0 |
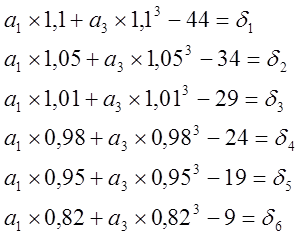 |
Левые и правые части уравнения (5) возводим в квадрат и складываем почленно.
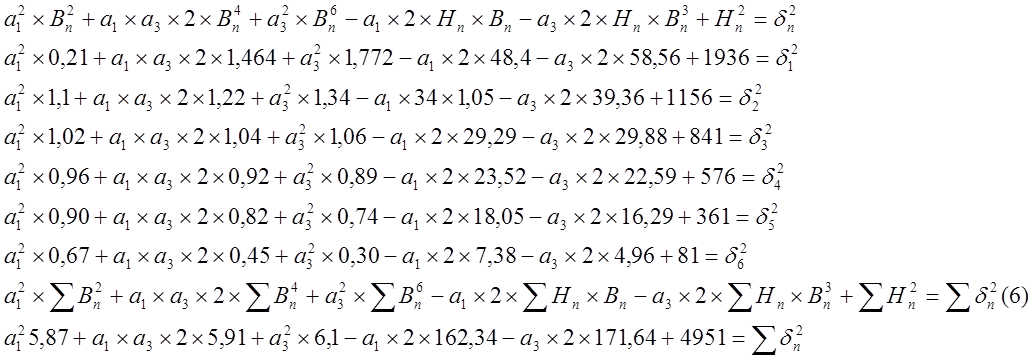
|
n\n |
H |
B |
B^2 |
B^4 |
B^6 |
H*B |
H*B^3 |
H^2 |
|
1 |
44 |
1,1 |
1,21 |
1,4641 |
1,771561 |
48,4 |
58,564 |
1936 |
|
2 |
34 |
1,05 |
1,1025 |
1,215506 |
1,340096 |
35,7 |
39,35925 |
1156 |
|
3 |
29 |
1,01 |
1,0201 |
1,040604 |
1,06152 |
29,29 |
29,87873 |
841 |
|
4 |
24 |
0,98 |
0,9604 |
0,922368 |
0,885842 |
23,52 |
22,58861 |
576 |
|
5 |
19 |
0,95 |
0,9025 |
0,814506 |
0,735092 |
18,05 |
16,29013 |
361 |
|
6 |
9 |
0,82 |
0,6724 |
0,452122 |
0,304007 |
7,38 |
4,962312 |
81 |
|
S |
5,8679 |
5,909206 |
6,098118 |
162,34 |
171,643 |
4951 |
Находим производные по а1 и а3.
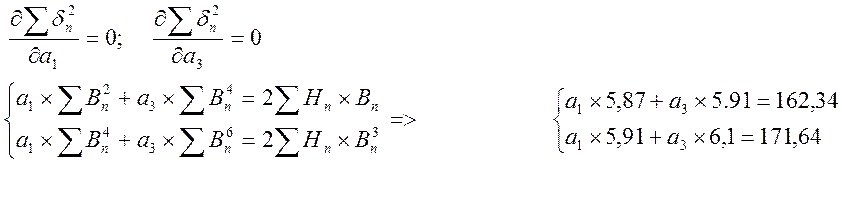
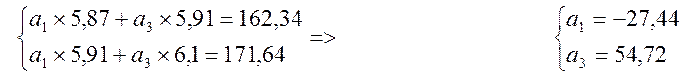
Из уравнения
определили коэффициенты а1 и а3. Подставляем в уравнение
значения а1 и а3, найдем величину ![]() ,
затем определяем
,
затем определяем ![]() .
.
![]()
![]()
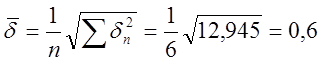 |
![]()
По данным из таблицы строим аппроксимирующую кривую
|
B |
1,1 |
1,05 |
1,01 |
0,98 |
0,95 |
0,82 |
0 |
|
Hисх |
44 |
34 |
29 |
24 |
19 |
9 |
0 |
|
Hапр |
42,64 |
34,53 |
28,66 |
24,61 |
20,84 |
7,67 |
0 |
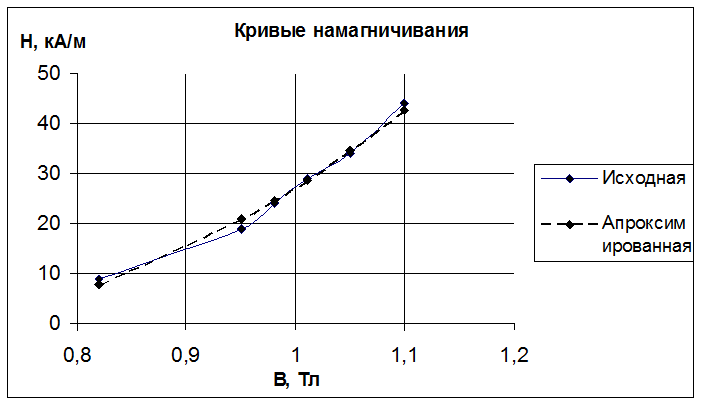
Рис.5
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.