Анализ методов автонастройки сложных систем, страница 2

Как детерминированный, так и статистический подходы к распознаванию образов имеют свои достоинства и недостатки. Соединить достоинства обоих подходов и обойти их недостатки – такая задача поставлена в работе [2] и сделана попытка ее решения в рамках детерминированно-статистического подхода. Суть такого подхода состоит в следующем. Как было отмечено выше, задача обучения распознаванию сводится к нахождению разделяющей функции и построению на ее основе решающего правила. Качество решающего правила определяется числом и соотношением различных типов ошибок при распознавании обучающегося образа. Отсутствие на практике априорных сведений о многомерных распределениях образов наряду с недостаточным объемом обучающей выборки не позволяет для нахождения решающего правила воспользоваться классическими методами теории статистических решений. В то же время весьма важно, чтобы решающее правило было наиболее простым. Эти обстоятельства обусловили разбиение процесса построения решающего правила на два этапа. На первом этапе при условии непересекаемости классов распознавания в пространстве C строится наиболее простое решающее правило, которое обеспечивает безошибочное распознавание реализации обучающей выборки. Наиболее подходящим методом для этой цели является детерминированный метод эталонов. В геометрической интерпретации  данного метода область образа сколь угодно сложной конфигурации строится из простых геометрических тел (эталонов). Первоначально эталоны строятся для каждой реализации обучающей выборки, обеспечивая попадание в них реализаций “чужих” образов. Используя далее аппарат минимизациии дизъюктивных  нормальных форм булевых функций, количество эталонов необходимых доя безошибочного распознавания обучающей выборки, удается существенно минимизировать.

Для минимизации числа ошибок и прогноза их величин при распознавании на втором этапе построения решающего правила производится непараметрическая статистическая коррекция решающего правила. Для такой коррекции используют два одномерных параметра, оценки которых можно получить по обучающей выборке, принадлежность реализаций которой классам распознавания заранее известна. Это максимально возможный выброс реализаций за “свою” эталонную оболочку и максимально возможное проникновение вглубь эталонных оболочек реализаций “чужих” образов. Эти параметры и позволяют строить непересекающиеся покрытия областей различных образов с минимальной областью альтернативных ошибок. В [2] приведены приложения данного подхода для решения ряда технических задач. Несмотря на перспективность детерминированно-статистического подхода, приведенные в [2] алгоритмы построения эталонов являются недостаточно формализованными, что затрудняет их машинную реализацию, особенно при часто встречающихся на практике случаях пересекаемости классов распознавания.

Определенный вклад в развитие современной теории автоматической классификации внесли научные коллективы, возглавляемые Э.Дидэ (Франция) [6] и С.А.Айвазяном (СССР) [5] . Так в работе [6] изложен непараметрический метод разбиения пространства C на классы, названный методом динамических сгущений (МДС). Суть метода в следующем. Рассматривая пространство  C  как покрытие, каждый элемент которого представляет собой вектор  _,  где Card , задав на нем структуру путем выбора представительства  и отображения . При этом отображение D является мерой сходства между объектом  и представителем . Приняв , т.е. множество разбиений на M классов, в качестве критерия оптимизации (как для дискриминантного анализа, так и для кластер-анализа) предложено отображение:

                               .

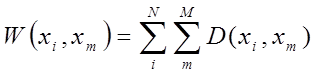Отображение измеряет таким образом “степень адекватности” между разбиением и представительством его классов . Задача оптимизации обучения формулируется в [6] следующим образом: найти среди всех элементов  такой элемент, который минимизирует W, принимающее лишь положительные значения. Алгоритм МДС состоит в последовательном итеративном нахождении функции представительства g, ставящей в соответствие подмножеству  определенное представительство, и функции назначения f, ставящей в соответствие одному или нескольким представительствам подмножества .

Поскольку топологический критерий является критерием первого рода, то это неизбежно ставит проблему исследования сходимости алгоритма. В работе [6] получено с позиций многомерного статистического анализа обобщение частных случаев алгоритма МДС в иерархической структуре многообразия алгоритмов автоматической классификации.

Общим недостатком известных методов распознавания, снижающим их практическую полезность, является отсутствие алгоритмов оптимизации процесса обучения по прямым критериям функциональной эффективности ОРС. Подтверждением этого является малочисленность публикаций с описанием рабочих алгоритмов обучения, что объясняется не только коммерческой тайной и повышенным вниманием оборонных ведомств к данной области. Основная причина отставания разработки высокоэффективных ОРС состоит в том, что в настоящее время, по мнению ряда авторов [5,6], отсутствует общая теория автоматического распознавания образов, несмотря на большое количество научных публикаций.