Синтаксический анализ. Дерево грамматического разбора (вывод) Основная задача синтаксического анализа

Синтаксический анализ

 

Формальные грамматики

G = {A _t ,A _n ,S ,P}

·  A _t  – алфавит терминальных символов

·  A _n –алфавит нетерминальных символов

·  S – начального нетерминального символа

·  P – система правил подстановки

1. S : 0 S 0
2. S : 1 S 1
3. S : 0
4. S : 1
5. S : ε

Основные определения.

Цепочка m непосредственно выводится из цепочки h  (обозначается так: h®m), если:

1.  h = ω α ψ (ω и ψ произвольные, возможно пустые цепочки);

2.  m = ω β ψ (ω и ψ – те же самые цепочки);

3.  в системе порождающих правил P есть правило α : β.

Тогда, подставив β вместо α в цепочке h= ω α δ, мы получим ω β δ, т.е. цепочку m.

Обратная подстановка не подразумевается, т.е. из возможности непосредственного вывода h®m не следует возможность непосредственного вывода m®h.

Примеры:

S ®1 S 1

1 S 1 ®1 0 S 0 1

Цепочка m просто выводится из цепочки d(dÞm), если существует последовательность непосредственных выводов:

d®d₁®d₂®d₃ ... d_n®m

Обозначается:dÞm

Пример:

S Þ1 0 S 0 1

Правильным предложениемязыка L, определяемого грамматикой G, называется цепочка, содержащая только терминальные символы и выводимая из начального нетерминала S.

Пример правильного предложения в грамматике двоичных чисел-перевертышей:

S Þ1 0 1 0 1

Дерево грамматического разбора (вывод):

 

Грамматика G a1		Грамматика G a2
1	S : S + T	1	S : U R
2	S : T	2	R : + S
3	T : T * F	3	R :
4	T : F	4	U : V W
5	F : ( S )	5	W : * U
6	F : i <идентификатор>	6	W :
7	F : c <константа>	7	V : ( S )
		8	V : i <идентификатор>
		9	V : c <константа>

Для G _a1:

S ® T ® T*F ® F*F ® (S)*F ® (S+T)*F ® (T+T)*F ® (F+T)*F ® (a+T)*F ® (a+F)*F ® (a+b)*F ® (a+b)*c

Для G_a2:

S ® UR ® VWR ® (S)WR ® (UR)WR ® (VWR)WR ® (aWR)WR ® (aR)WR ® (a+S)WR ® (a+UR)WR ® (a+VWR)WR ® (a+bWR)WR ® (a+bR)WR ® (a+b)WR ® (a+b)*UR ® (a+b)*VWR ® (a+b)*cWR ® (a+b)*cR ® (a+b)*c

Основная задача синтаксического анализа:

 

Классификация формальных грамматик

Класс 0 – общие

нет ограничений на вид правил.

Класс 1 – контекстно-зависимые

в любом правиле длина цепочки левой части не больше длины цепочки правой части.

Класс 2 – контекстно-свободные

в левой части любого правила ровно один нетерминал, на правые части ограничений нет.

Класс 3 – регулярные

в левой части любого правила ровно один нетерминал, в правой части не более одного нетерминала.

Свойства контекстно-свободных грамматик и символов грамматики

Рекурсия

                                                                                                X Þ α X β

                                                                        Левая:                                                                        X Þ X β

                                                                        Правая:                                                                        X Þ α X

                                                                        Общая (простая):                                                                        X Þ α X β

                                                                        Прямая общая:                                                                        X ® α X β                                                                        ( X : α X β )

                                                                        Прямая левая:                                                                        X ® X β                                                                        ( X : X β )

                                                                        Прямая правая:                                                                        X ® α X                                                                        ( X : α X )

                                                                        Косвенная:                                                                                        (  X  : α ₁ Y ₁ β ₁

Y ₁ : α ₂ Y ₂ β ₂

  ...

Y _n : α _n+1 X β _n+1

)

Нетерминал может быть:                           нерекурсивным / рекурсивным

Рекурсивный нетерминал может быть:   леворекурсивным / праворекурсивным / просто рекурсивным

                                                                           Возможны все сочетания:

                                                                                  лево + право

                                                                                  лево + просто

                                                                                  право + просто

                                                                                  лево + право +просто

                                                                      пряморекурсивным / косвенно рекурсивным (может быть одновременно и прямо и косвенно)

Однозначность

Грамматика Ga3
1	S : S + S
2	S : T
3	T : T * T
4	T : F
5	F : ( S )
6	F : ident
7	F : const

a+b+c

S ® S+ S ® T+S ® F+S ® a+S ® a+S+S ® a+T+S ® a+F+S ® a+b+S ® a+b+T ® a+b+F ® a+b+c

S ® S+S ® S+S+S ® T+S+S ® F+S+S ® a+S+S ® a+T+S ® a+F+S ® a+b+S ® a+b+T ® a+b+F ® a+b+c

 

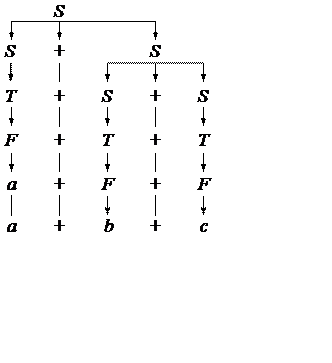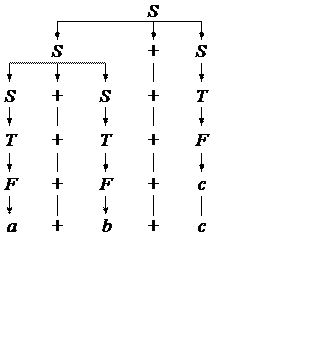a+(b+c)                                                (a+b)+c

G _a1:

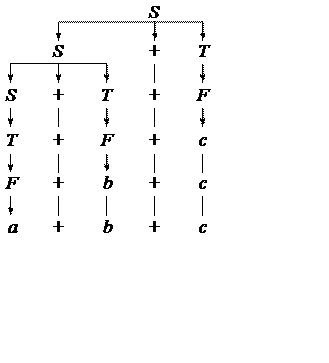S ® S+T ® S+T+T ® T+T+T ® F+T+T ® a+T+T ® a+F+T ® a+b+T ® a+b+F ® a+b+c

S ® S+T ® S+F ® S+c ® S+T+c ® S+F+c ® S+b+c ® T+b+c ® F+b+c ® a+b+c

(a+b)+c

G _a2:

S ® UR ® VWR ® aWR ® aR ® a+S ® a+UR ® a+VWR ® a+bWR ® a+bR ® a+b+S ® a+b+UR

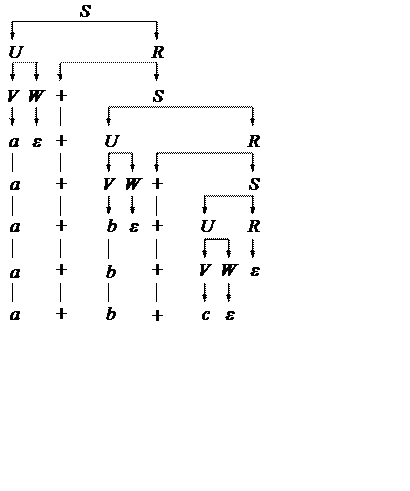® a+b+VWR ® a+b+cWR ® a+b+cR ® a+b+c

S ® UR ® U+S ® U+UR ® U+U+S ® U+U+UR ® U+U+U ® U+U+VW ® U+U+V

® U+U+c ® U+VW+c ® U+V+c ® U+b+c ® VW+b+c ® V+b+c ® a+b+c

a+(b+c)

Свойства символов грамматики

Аннулируемость

X Þ ε

Недостижимость

Бесплодность