Преобразование недетерминированного неоптимального автомата в детерминированный оптимальный, страница 2

Критерии 2, 3. Преобразование недетерминированного КА в детерминированный

Подготовка: формирование начального неотмеченного множества вершин

 

образование множества неотмеченных множеств вершин (вначале включающего только начальное множество)

и вначале пустого множества отмеченных множеств вершин

Основной цикл: перебор всех неотмеченных множеств в произвольном порядке

Первый шаг: удаление взятого множества вершин из множества неотмеченных множеств,

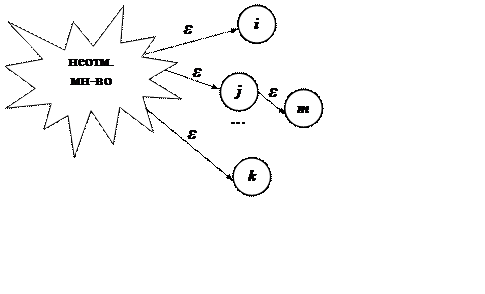
построение ε – замыкания взятого множества

(учитываются только ε – переходы в рабочие вершины)

 

Второй шаг: поиск сформированного ε – замыкания в множестве отмеченных множеств, присвоение отметки (номера) и добавление в множество отмеченных множеств, если в нем нет в точности такого же множества вершин

Третий шаг (выполняется только для вновь добавленного отмеченного множества):

определение набора символов, помечающих все выходящие из вершин множества дуги {a,b, … ε} (в том числе учитывается и символ ε, помечающий дуги переходов в финальные вершины)

Внутренний цикл: перебор всех символов набора, построение новых неотмеченных множеств

 

Запоминание дуги перехода из отмеченного множества в новое не отмеченное множество по символу a

После завершения основного цикла:

1.  Сопоставление каждому отмеченному множеству вершин исходного графа в точности одной вершины нового графа. Если в отмеченном множестве есть хотя бы одна финальная вершина, то и ассоциированная с ним вершина нового графа считается финальной.

2.  Формирование дуг переходов в новом графе на основе информации о переходах из одного множества вершин в другое.

 

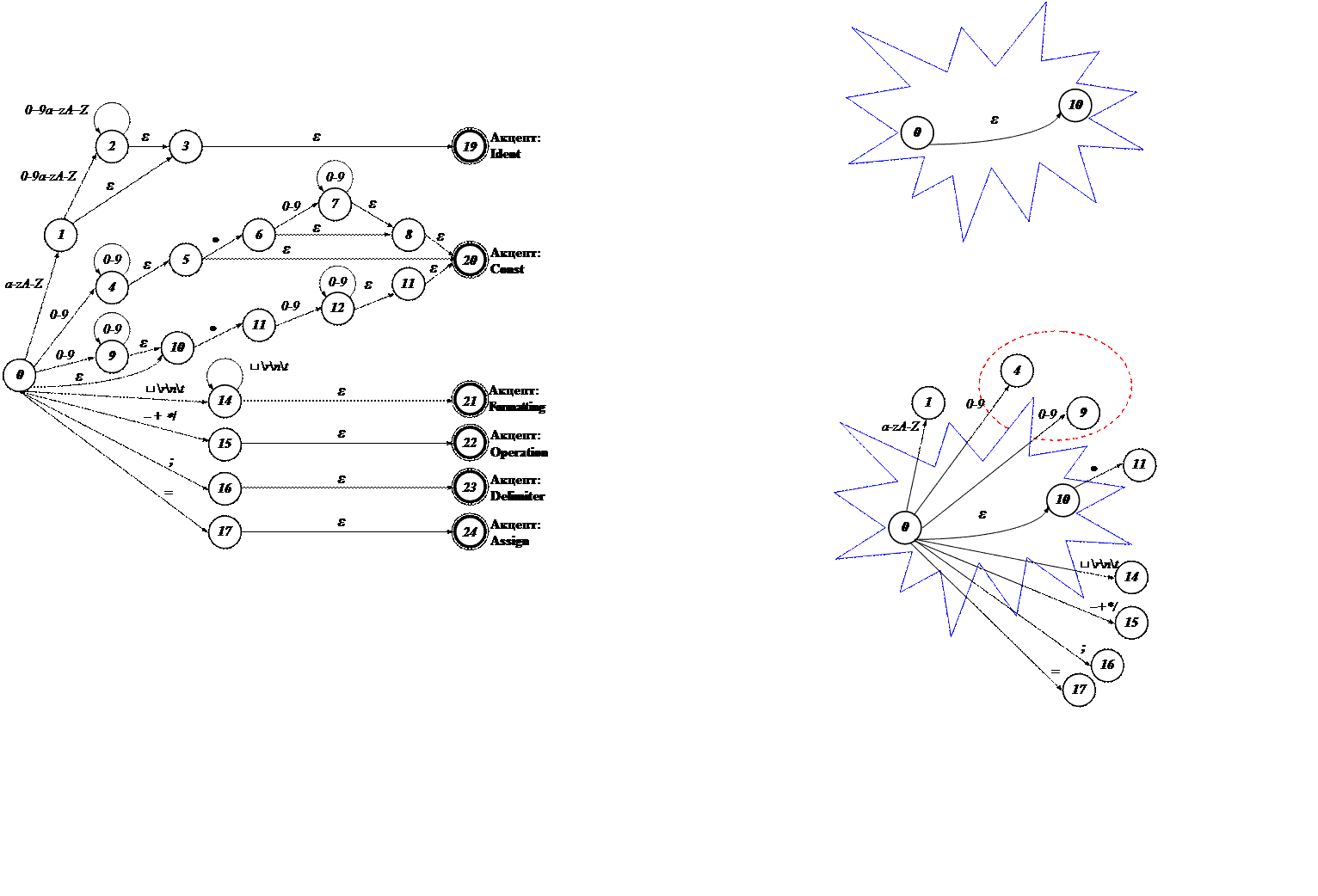
Критерий 4. Обнаружение и ликвидация тупиковых состояний

Т.1.  С каждой строкой i управляющей таблицы сопоставляется список S_i (в начальный момент – пустой) финальных состояний, достижимых из данного состояния;

Т.2.  Начиная с нулевой, просматриваются все строки таблицы;

Т.3.  В каждой строке (пусть ее номер n) просматриваются все клетки;

Т.4.  Если клетка не пуста и содержит номер финального состояния, то этот номер добавляется к списку S_n, если его нет в этом списке;

Т.5.  Если клетка не пуста и содержит номер рабочего состояния k (k не равно n), то все элементы списка S_k финальных состояний строки k добавляются к списку S_n финальных состояний строки n (естественно, если их нет в списке S_n);

Т.6.  Если была просмотрена последняя строка рабочей зоны и в процессе просмотра изменился хотя бы один список S_i, то нужно вернуться к шагу Т.2, иначе процесс завершается.

Тупиковыми будут состояния с пустыми списками S_i

Все тупиковые состояния (вместе с переходами в эти состояния и из этих состояний) должны быть удалены.

Критерий 5. Обнаружение и ликвидация недостижимых состояний

Н.1.  Сопоставим с каждой строкой рабочей зоны управляющей таблицы (кроме нулевой строки) отметку «недостижима», а с нулевой строкой – отметку «достижима»;

Н.2.  Начиная с нулевой, просмотрим все «достижимые» строки таблицы;

Н.3.  В каждой такой строке просмотрим все клетки и, если в клетке находится номер рабочего состояния k, то значение отметки строки k изменим на значение «достижима»;

Н.4.  Если просмотрена последняя строка таблицы и хотя бы для одной строки отметка изменилась со значения «недостижима» на значение «достижима» – вернуться к шагу Н.2, иначе процесс завершается.

Все недостижимые состояния (вместе с переходами в эти состояния и из этих состояний) должны быть удалены.

Критерий 6. Обнаружение и слияние эквивалентных состояний

Эквивалентными являются такие состояния, все переходы из которых либо строго совпадают, либо различаются только переходами друг на друга.

 

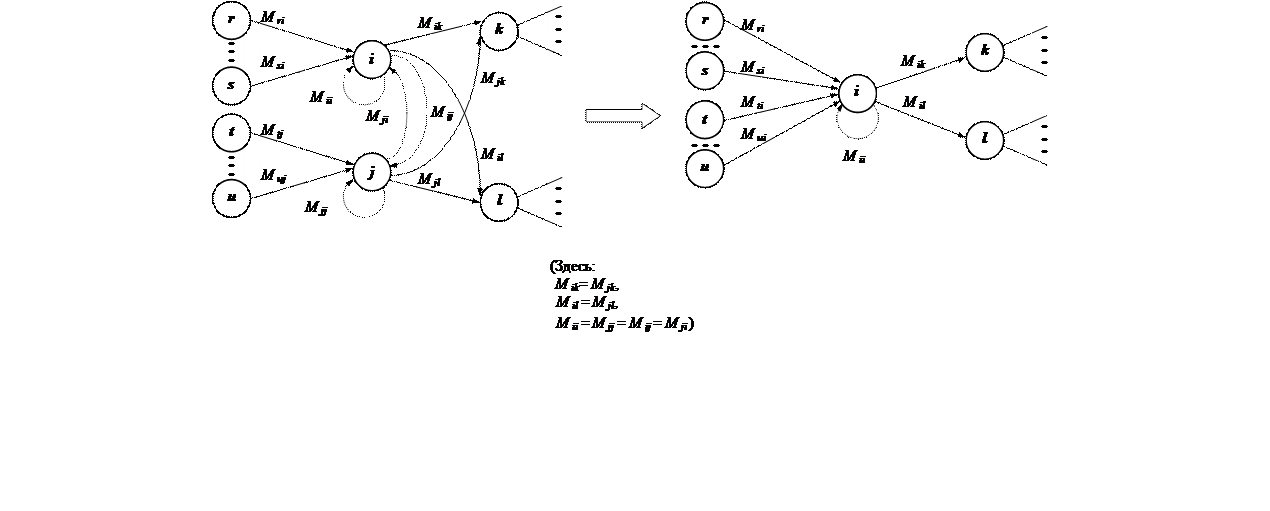Критерий 7. Слияние одинаковых колонок

ГСП и УТ детерминированного и почти оптимального КА: