Потоки Пальма и потоки Эрланга. Их модели и свойства

69. Потоки Пальма и потоки Эрланга. Их модели и свойства.

Опр. Потоком Пальма называется поток обладающий свойствами ординарности, стационарности и независимости интервала времени Т между событиями. Требование независимости интервала Т является более слабым, чем требование без последействия, поэтому такие потоки называют с ограниченным последействием.

Теорема: Пусть в систему поступает поток требований типа Пальма. Заявка, заставшая все каналы занятыми получает отказ. Поток требований, получивших отказ также является потоком Пальма

Еще одним примером потоков Пальма являются потоки Эрланда, которые могут быть получены следующим образом: если из простейшего потока исключается каждое второе требование, то оставшийся поток образует поток второго порядка (Эрланда). Если из потока сохраняется каждое 3 требование, то такой поток называется потоком 3 порядка и так далее.

            Для потоков k-го порядка интервалы времени распределены по следующему закону:

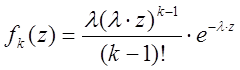, с увеличением порядка функция f(z) – убывает М[T] = K/l, D[T]=K/l²

При достаточно большом (К>=5) поток Эрланда К-го порядка можно считать нормальным с указанными выше мат. ожиданием и дисперсией. Это следует из того, что интервал времени между двумя последовательными событиями в потоке Эрланда К-го порядка представляет собой сумму К независимых СВ с одним законом распределения. Доказательство этого утверждения следует из центральной предельной теоремы теории вероятности.

            Задавая различные значения К можно получать потоки, обладающие различным последействием от полного его отсутствия до полной функциональной связи между моментами появления событий.

            На самом деле при К=1 получаем простейший поток, а при К равном бесконечности поток Эрланда приблизился к регулярному потоку.