Схемы на ОУ могут выполнять математические операции над входными сигналами. При всех минусах аналоговых вычислительных устройств аналоговая обработка сигналов может иметь преимущества в тех случаях, когда цифровая занимает слишком много времени, либо требует больших аппаратных затрат, либо не требуется высокая точность результатов. При использовании в различных вычислительных устройствах ОУ охватываются глубокой отрицательной обратной связью, а на входы могут включаться различные элементы. Такая схема, состоящая из ОУ, внешних элементов на входе и в цепи обратной связи называется решающим усилителем.
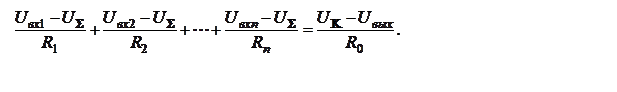 Усилитель может суммировать несколько входных
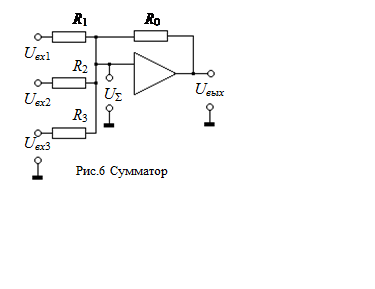
напряжений. На рис.6 представлен сумматор,
реализованный на базе усилителя с одним входом. С учетом ранее перечисленных
требований на основании закона Кирхгофа сумма токов, протекающих через входные
резисторы, равна току, протекающему через резистор обратной связи:
Усилитель может суммировать несколько входных
напряжений. На рис.6 представлен сумматор,
реализованный на базе усилителя с одним входом. С учетом ранее перечисленных
требований на основании закона Кирхгофа сумма токов, протекающих через входные
резисторы, равна току, протекающему через резистор обратной связи:
Напряжение
на выходе ОУ равно ![]()
Совместное решение уравнений в результате исключения величины UΣ дает выражение для выходного напряжения:
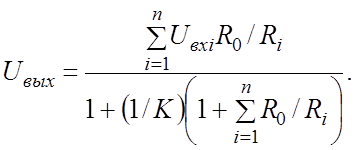
Поскольку коэффициент усиления ОУ очень велик, то при одинаковом порядке значений резисторов на входе и в обратной связи, можно принять, что
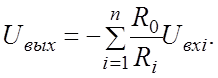
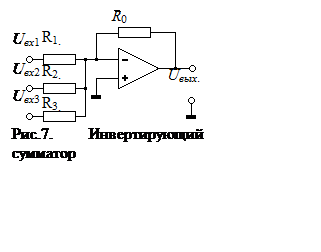 На рис.7 приведена схема инвертирующего
сумматора, построенная на базе дифференциального ОУ. Выходное напряжение Uвых равно:
На рис.7 приведена схема инвертирующего
сумматора, построенная на базе дифференциального ОУ. Выходное напряжение Uвых равно:
![]()
![]()
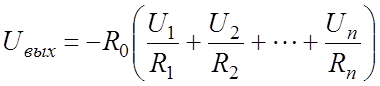 .
.
 Отношение резисторов R0 и Ri задают значения
коэффициентов передачи по соответствующим входам. Вместо резисторов могут быть
использованы другие элементы, например, конденсаторы. При этом предполагается,
что ОУ идеален.
Отношение резисторов R0 и Ri задают значения
коэффициентов передачи по соответствующим входам. Вместо резисторов могут быть
использованы другие элементы, например, конденсаторы. При этом предполагается,
что ОУ идеален.
На основе схемы неинвертирующего усилителя можно построить неинвертирующий сумматор (рис.8). Выходное напряжение такого усилителя равно:
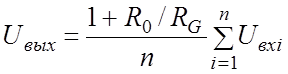 .
.
Для получения суммы входных напряжений с коэффициентом пропорциональности, равным единице, необходимо выполнить равенство (1+R0/RG)/n = 1, откуда R0/RG = n – 1. Так, если входных сигналов два, то R0 = RG; если три, т.е. n = 3, то R0 = 2RG.
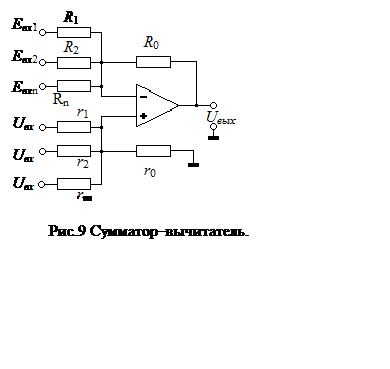 Если объединить схемы рис.7 и рис.8,
получим сумматор – вычитатель (см. рис.9). Напряжение на его выходе равно:
Если объединить схемы рис.7 и рис.8,
получим сумматор – вычитатель (см. рис.9). Напряжение на его выходе равно:
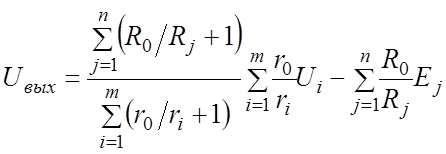 .
.
В частном случае, когда значения всех резисторов одинаковы, получим:
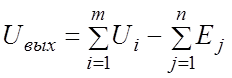 .
.
Погрешности операции суммирования определяются погрешностями, возникающими из-за конечного значения коэффициента усиления ОУ, дрейфа нуля ОУ, неточностей изготовления резисторов, входного тока ОУ и динамическими погрешностями.
Погрешности от конечного значения коэффициента
усиления ОУ. Выражение для значения выходного напряжения суммирующего ОУ
показывает, что чем больше коэффициент усиления, тем точнее работает схема.
Абсолютная погрешность схемы определяется разностью двух значений выходного
напряжения–точного и приближенного ΔUK = Uвых
Н – Uвых Т, а
относительная погрешность равна: 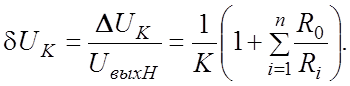 Исходя из величины допустимой погрешности,
можно рассчитать необходимый коэффициент усиления ОУ
Исходя из величины допустимой погрешности,
можно рассчитать необходимый коэффициент усиления ОУ
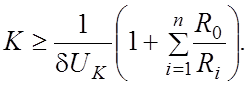
Погрешность от дрейфа нуля ОУ. Одну из
основных погрешностей работы ОУ создает дрейф нуля. Это медленно меняющееся
напряжение на выходе ОУ при неизменном входном, в том числе и при равном нулю.
Не приводя всех выкладок и полагая, что коэффициент усиления достаточно велик,
погрешность выходного напряжения от дрейфа нуля равна: ![]() где Uдр(t)–приведенный ко входу дрейф нуля. Это
такое напряжение, которое следует подать на вход ОУ в каждый данный момент
времени, чтобы компенсировать погрешность ΔUдр(t).
где Uдр(t)–приведенный ко входу дрейф нуля. Это
такое напряжение, которое следует подать на вход ОУ в каждый данный момент
времени, чтобы компенсировать погрешность ΔUдр(t).
Погрешность от неточного изготовления резисторов. Эта погрешность может быть вычислена по формуле:
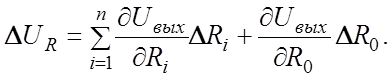
Считая усилитель идеальным,
получим 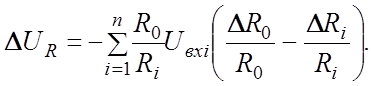
Погрешность от входного тока усилителя. Общая формула суммирующего усилителя выведена в предположении, что входной ток усилителя равен нулю. В действительности, он имеет определенное значение и вносит погрешность. Положив Uвх = 0 и UΣ = 0, получим ΔUвхi = iвхR0.
Общая абсолютная погрешность суммирующего усилителя равна сумме её составляющих: ΔU = ΔUK+ ΔUдр+ ΔUR+ ΔUвхi.
Дифференциальный усилитель, как и ОУ с одним входом, вследствие неидеальности характеристик вносит погрешность при выполнении математических операций. Помимо погрешностей, вносимых конечным значением коэффициента усиления, дрейфом нуля ОУ, наличием ненулевого входного тока ОУ, первичными погрешностями элементов цепи обратной связи, дифференциальный усилитель имеет специфические параметры, влияющие на точность работы решающего усилителя:
разностный входной ток Diвх–разность токов по входам усилителя, измеренная при напряжении на выходе, равном нулю. Значение Diвх может достигать нескольких мкА.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.