Нисходящий автомат с одним состоянием, управляемый входным символом и символом, находящимся на верхушке стека, страница 2

Способ реализации		Тактов	Среднее
1	Процедурная реализация	31	3.875
2	Автомат с несколькими состояниями	71	8.875
3	Оптимизированный автомат	52	6.5
4	Автомат с одним состоянием	21	2.625

Способ реализации		Клеток	Полей/операций
2	Автомат с несколькими состояниями	33	6 (полей)
3	Оптимизированный автомат	23	6 (полей)
4	Автомат с одним состоянием	49	До 4 (операций)

Основная идея восходящего восстановления
дерева грамматического разбора

Грамматика G a1
1	S : S + T
2	S : T
3	T : T * F
4	T : F
5	F : ( S )
6	F : i <идентификатор>
7	F : c <константа>

Временно считаем, что в грамматике нет правил вида N : e

Перед последним шагом:

Предложение: x+ y* z

S + T

Должно существовать правило S : b ^n–1

Цепочку b ^n-1 далее будем называть основой.

После последнего шага:

 

Операцию замены основы нетерминалом из левой части правила будем называть сверткой.

Заметим, что цепочку b ^n-1 можно рассматривать и так: ε  b ^n–1 ε ,

а следовательно и так: j ^n–1 b ^n–1 y ^n–1 (j ^n–1=ε, y ^n–1=ε)

Перед промежуточным шагом:

S + F * z

-  цепочка j ^i–1 ( S + ) не содержит никакой основы, т.е. ни одной правой части правила грамматики,
 в остальном – произвольна (возможно, пуста);

-  цепочка y ^i–1 ( * z ) произвольна.

-  цепочка b ^i–1 ( F ) есть основа (является правой частью некоторого правила N : b ^i–1, здесь T : F);

Заметим, что в принципе возможна ситуация, когда на текущем уровне можно увидеть не одну, а две или более основы:

j₁^i–1 b^i–1 y₁^i–1 , где b^i–1 – правая часть правила N : b^i–1

j₂^i–1 γ^i–1 y₂^i–1 , где γ^i–1 –  правая часть правила M : γ^i–1

После свертки по правилу T : F имеем S + T * z:

j₁^i–1 =eb^i–1 = S + T        y₁^i–1= * z

j₂^i–1 =S +γ^i–1 = T               y₂^i–1= * z

Это приводит (потенциально) к неоднозначности выбора основы для свертки и называется конфликтом
«свертка / свертка»

После промежуточного шага (свертки по правилу :

S + T * z

В цепочке j ^i–1 N  y ^i–1 найдем самую левую основу и представим эту цепочку в виде j ⁱ bⁱ y ⁱ.

Заметим, что найденная новая основа может находиться где угодно, в том числе левее свернутой ( | j ⁱ | < | j ^i-1 | ),
правее ( | j ⁱ | > | j ^i-1 | ), или там же ( | j ⁱ | = | j ^i-1 | ).

И, наконец, перед первым шагом:

j ⁰ =eb ⁰ = x                                                                                                           y ⁰ =+ y* z

В результате замены b ⁰ на  R:

 

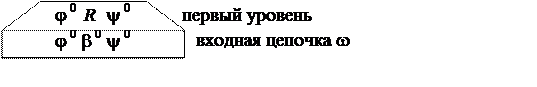j ⁰ =eR = F                                                                                                           y ⁰ = + y* z

Находим самую левую основу:

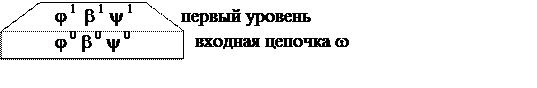j ⁰ =eb ⁰ = F                                                                                                           y ⁰ =+ y* z

 Алгоритм восходящего восстановления дерева разбора,

первая редакция

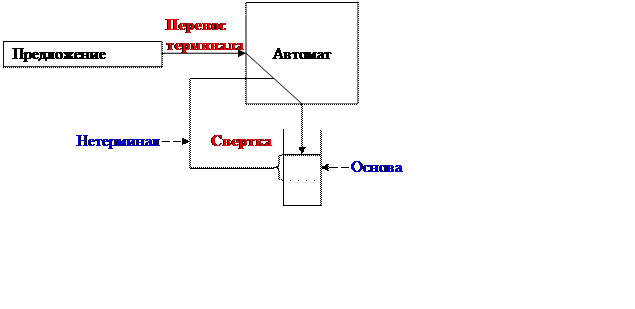
Используется стек символов, вначале пустой.

Вводим (временно) понятие операции Перенос, перемещающей символ со входа автомата на верхушку стека.

Будем обозначать эту операцию буквой S (от слова Shift – перемещение, перенос, сдвиг)

Основы могут находиться на верхушке стека (последним символом правой части правила вверху).

Операция Свертка снимает основу со стека и помещает нетерминал из левой части правила на верхушку стека (этот смысл операции опять же временно).

Эту операцию будем обозначать буквой R_m (от слова Reduce – свертка) с параметром m, обозначающим номер правила.

Если цепочка w u будет свернута в цепочку S u, то предложение w правильно, иначе – в предложении w ошибка.

			В УП не так