Модели триггеров. Динамическое управление записью, страница 3

Ранее (лекция 8) мы уже отмечали, что модель цифровой схемы можно представить системой булевских уравнений: для каждого логического элемента - своё уравнение. Порядок записи уравнений в системе может быть произвольным и это не должно влиять на результаты моделирования, хотя интуитивно понятно, что они должны следовать в порядке срабатывания реальных элементов в реальной схеме.

В таблице 1 показано, как может выглядеть булевская модель стробируемого RS-триггера, показанного на рис.1,б. Уравнения записаны в произвольном порядке в формате языка моделирования PML пакета PCAD.

В исходном состоянии (такт Т0) на входы триггера подан пассивный набор сигналов (S = C = R = 0). Триггер находится в режиме хранения, и для определённости примем, что в нём записана «1» . Если просчитать систему булевских уравнений для названных условий, то будет ещё раз подтверждён вектор

исходного состояния на всех четырёх выходах (Q=1, NQ=0, F0=1, F1=1).

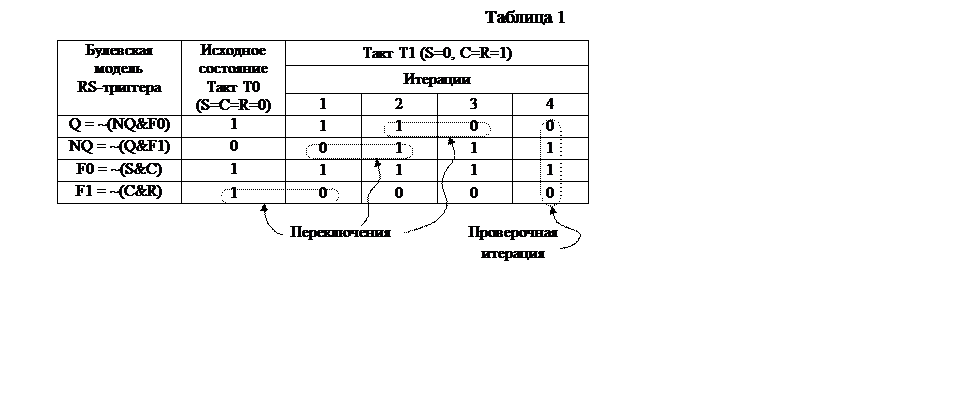В следующем цикле работы моделятора (такт Т1) на входы триггера подаётся набор входных сигналов (S=0, C=R=1), который должен сбросить его в состояние «0». Однако, выполнив первый прогон модели (третий столбец таблицы), мы обнаруживаем, что результаты моделирования не соответствуют действительности: на выходе по-прежнему Q = 1. Правильно переключился лишь выход F1.

Моделятор сравнивает полученный вектор результатов с предыдущим (в данном случае с вектором исходного состояния) и убеждается, что они не совпадают. Это означает, что итерационный процесс вычисления результата моделирования на текущем такте не закончен, и следует повторить прогон модели.

Заметим, что повторные прогоны модели осуществляются для одного и того же набора входных данных (в нашем примере – для такта Т1). Понятно, что и модельное время остаётся прежним.

Повторные прогоны модели на неизменном наборе входных данных называются итерациями. Они длятся до тех пор, пока не совпадут результаты двух соседних итераций, что свидетельствует об окончании переходных процессов в моделируемой схеме. В нашем примере – это третья и четвёртая итерации. Последняя итерация не даёт никаких новых результатов, но она нужна, чтобы убедиться в окончании вычислительного процесса на текущем такте. По этой причине её называют проверочной итерацией.

Итерационный характер получения результатов моделирования является серьёзным недостатком рассмотренного метода, так как в несколько раз увеличивает общее время модельного эксперимента. В дальнейшем мы узнаем, что ранжированием цифровых схем можно существенно уменьшить требуемое число итераций, а для комбинационных схем и вовсе избавиться от них.

Добавим, что в современных АСМ, использующих событийный метод моделирования и модели элементов, учитывающие временные задержки, об итерациях можно вспоминать лишь как о кошмарных пережитках недалёкого прошлого.

Подводя итог обсуждению структурных моделей триггеров, можно констатировать, что они имеют два серьёзных недостатка:

§  длительное время моделирования из-за низкоуровневого описания (на уровне логических вентилей);

§  наличие итераций, то есть многократных прогонов модели на неизменном наборе входных данных, что в конце концов приводит к тому же результату – дополнительным временным затратам на моделирование.

К достоинствам структурных моделей триггеров следует отнести их повышенную точность и универсальность. Они позволяют без всяких «наворотов» имитировать неисправности отдельных элементов структуры, наблюдать реакцию схемы на запрещённые наборы входных сигналов, не беспокоиться о том, имеет ли триггер динамическое управление и как его отобразить в модели.

Аналитическая модель триггера представляет собой его характеристическое уравнение. Для рассматриваемого в качестве примера стробируемого RS-триггера она выглядит следующим образом:

при выполнении условия  S*R = 0:

Q_NEW = S*C + Q_OLD* ~(R*C),

NQ_NEW = ~Q_NEW.

Здесь:

Q_NEW – новое (будущее) состояние триггера;

Q_OLD – старое (текущее) состояние триггера;