Множества выбора. Процедурная реализация рекурсивного спуска

 

N	:	a 1
N	:	a 2
...
N	:	a z

N y ^j–1 ® a _k y ^j–1 Þ t μ ^j–1.

 

Из a _k y ^j–1 выводятся цепочки, предшественники которых – это предшественники a _k.

Кроме того, если a _k – пустая цепочка или цепочка, состоящая только из аннулируемых нетерминалов, то из a _k y ^j–1Þy ^j–1 выводятся цепочки, предшественники которых принадлежат множеству последователей нетерминала N.

Множества выбора

1.  M _выб (N : a _k) = M _пр (a _k),                          если a _k содержит хотя бы один терминал или неаннулируемый нетерминал.

2.  M _выб (N : a _k) = M _посл (N),                         если a _k есть пустая цепочка.

3.  M _выб (N : a _k) = M _пр (a _k) ÈM _посл (N),      если a _k не пуста, но состоит только

Грамматика G a1				Грамматика G a2
	Правило	Способ	Множество		Правило	Способ	Множество
0	Z : S u			0	Z : S u
1	S : S + T	M пр(S + T)	(, i, c	1	S : U R	M пр(U R)	(, i, c
2	S : T	M пр(T)	(, i, c	2	R : + S	M пр(+ S)	+
3	T : T * F	M пр(T * F)	(, i, c	3	R : e	M посл(R)	), u
4	T : F	M пр(F)	(, i, c	4	U : V W	M пр(V W)	(, i, c
5	F : ( S )	M пр(( S ))	(	5	W : * U	M пр(* U)	*
6	F : i	M пр(i)	i	6	W : e	M посл(W)	+, ),u
7	F :c	M пр(c)	c	7	V : ( S )	M пр( ( S ) )	(
				8	V : i	M пр(i)	i
				9	V : c	M пр(c)	c

LL(1)-грамматики – такие, в которых попарно не пересекаются множества выбора всех правил с одинаковым нетерминалом в левых частях.

 

Процедурная реализация рекурсивного спуска

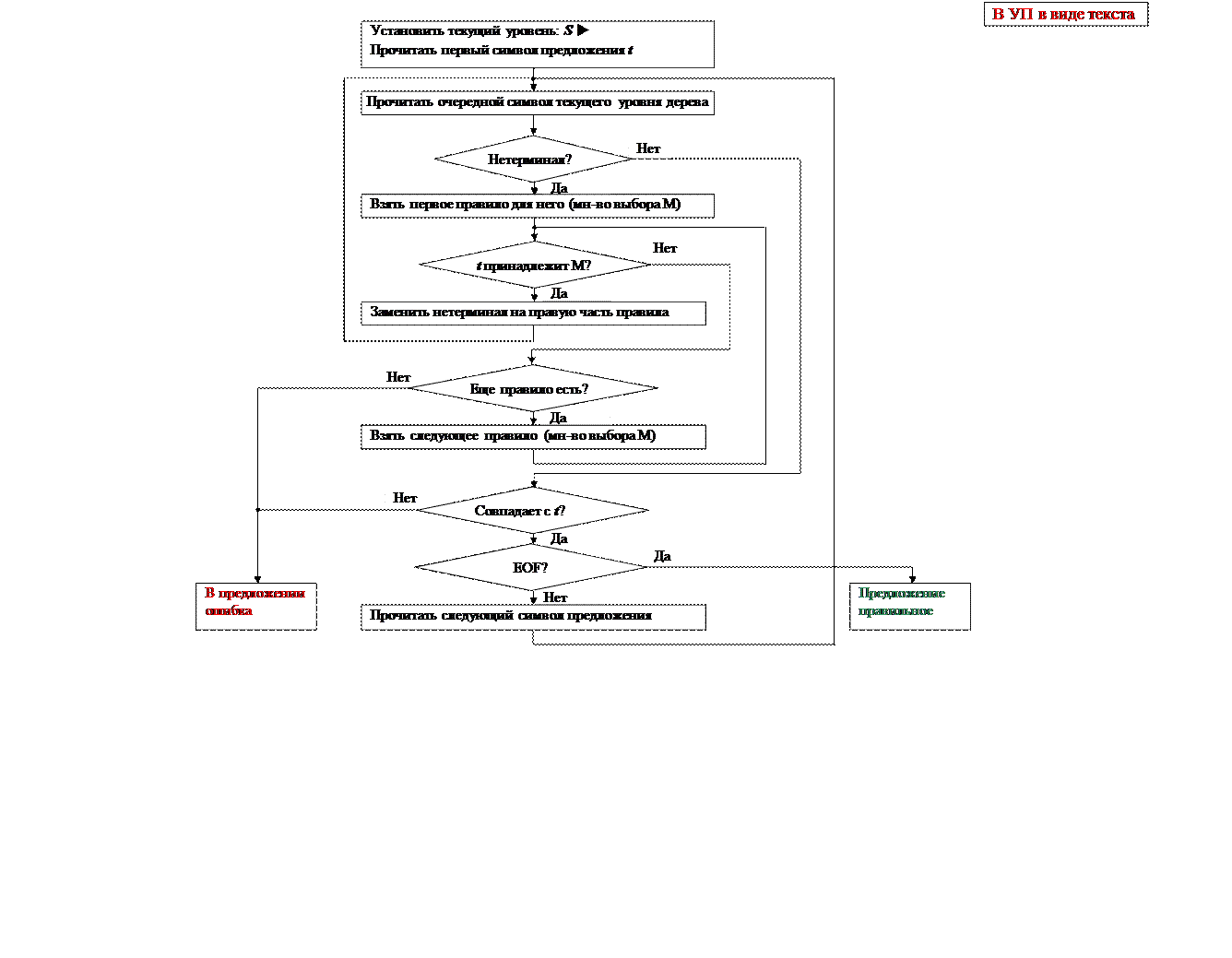
В ВебТрансЛабе – шаблоны с названием …SyntAsRD…

bool RecurciveDescent() {

CurrentLexem = GetLexem();    // прочитать первый терминал. GetLexem - вызов лексического анализатора

if ( S() == FALSE )                     // вызвать функцию S() для проверки всего предложения до EOF (EndOfFile)

return FALSE;                  // останов по ошибке, если предложение неверно

if ( CurrentLexem != EOF )       // после правильного предложения не  должно быть ничего, кроме конца файла

return FALSE;                  // если это не так – останов по ошибке

return TRUE;                              // предложение правильное, останов

}

bool S() {

if ( U() == FALSE )                    // вызываем функцию разбора нетерминала U

returnFALSE;                  // и останавливаемся, если она остановилась по ошибке

if ( R() == FALSE )                    // аналогично для нетерминала RВместо этой и двух следующих строк можно:

return FALSE;                  // return R();

return TRUE;                              // возврат

}

bool U() {

if ( V() == FALSE )                    // вызываем функцию разбора

return FALSE;                  // нетерминала V и останавливаемся, если она остановилась по ошибке

return W();                                  // возвращаем то, что вернет  функция W()

}

bool R() {

if ( CurrentLexem == ‘+’ ) {                     // очередной терминал входит в множество выбора правила R : + S

CurrentLexem = GetLexem();         // прочитаем следующий терминал

return S();                                        // и вызовем функцию S() с возвратом ее результата

}

if (( CurrentLexem == ‘)’) || ( CurrentLexem == EOF ))                                                                                            //очередной терминал входит в множество выбора правила R : e

return TRUE;        // применяем это правило, т. е. не делаем ничего и возвращаемся

return FALSE;                //очередной терминал не входит ни в одно множество выбора, поэтому останов по ошибке

}

bool W() {

if ( CurrentLexem == ‘*’ ) {                     // очередной терминал входит в множество выбора правила W : * U

CurrentLexem = GetLexem();         // прочитаем следующий терминал

return U();                                       // и вызовем функцию U() с возвратом ее результата

}

if ( ( CurrentLexem == ‘+’ ) || ( CurrentLexem == ‘)’ ) || ( CurrentLexem == EOF ) ) // очередной терминал входит

//в множество выбора правила W : e